本文主要是介绍欧拉函数确定1-n有多少个数和 n 互质详解 附C语言代码 蓝桥杯互质数的个数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
唯一分解定理
任意一个大于 1 的正整数都能被唯一地分解为质因数的乘积。
例如 8 = 2*2*2, 171 = 3*3*19, 30 = 2*3*5, 19 = 19。注意1既不是质数也不是合数。
为什么判断一个数是否是质数只要判断2-√n中有没有因数
24可以分解成 4*6,或者3*8,这两对因数中都是一个小于24的平方根,另一个大于,不可能两个数都小或者两个数都大,因此如果2-√n中找不到一个 n 的约数,那么在剩下的一半里也必定找不出两个数相乘等于 n,一定会是大于 n 的。
欧拉函数
解决的是1到 n 中有多少个数与 n 互质,函数长这样,看不懂先别急。
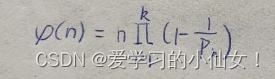
这一部分解释一下这个式子是怎么来的,可以跳过:
我们已知30 = 2*3*5,那么1-30中有多少个数与30互质就可以通过减去不和30互质的数得到,既然2、 3、 5不是,那他们的倍数也就不是,所以要减去 30/2、 30/3、 30/5,但是减的时候多减掉了2和3的公倍数、3和5的公倍数、2和5的公倍数,所以要再加上,就相当于有三个圆,两两相交,中间有一部分是三个圆重叠,所以还要再减去30/(2*3*5),最后整理一下就是 上面的式子了。

下面我们来看个例子:
8可以分解成2*2*2,1-8中与8互质的数的个数应该,8*(1-1/2) = 4,恰好是1、 3 、 5 、7这四个数,同样地 6 也是如此。完整代码在后面。

一个正整数可以分解成素因数的乘积的形式,所以我们找到一个素因数之后要一直除这个数,例如12=2*2*3,我们发现 2 是12 的因数之后要一直除2,直到剩下3,才能找到下一个素因数,才可以根据公式乘下一个(1-1/p)。
另外还有一种情况比较特殊,即这个数本身就是一个素数,例如19只能分解成19,所以在2到平方根这个范围内没有任何素因数,for循环结束后还剩n,最后的结果就是n*(1-1/n)。其他情况下最后n应该除尽了,变成1.
#include <stdio.h>
int main()
{ int n=0; scanf("%d", &n); int res = n; // 初始化结果为 n for (int i = 2; i * i <= n; i++) { if (n % i == 0) { res /= i * (i - 1); while (n % i == 0) // 将 n 中的该素因子全部除尽 { n /= i; } } } if (n > 1) { res = res / n * (n - 1); } printf("%d\n", res); return 0; }学到这个是因为暴力判断有点费时间。
这篇关于欧拉函数确定1-n有多少个数和 n 互质详解 附C语言代码 蓝桥杯互质数的个数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






