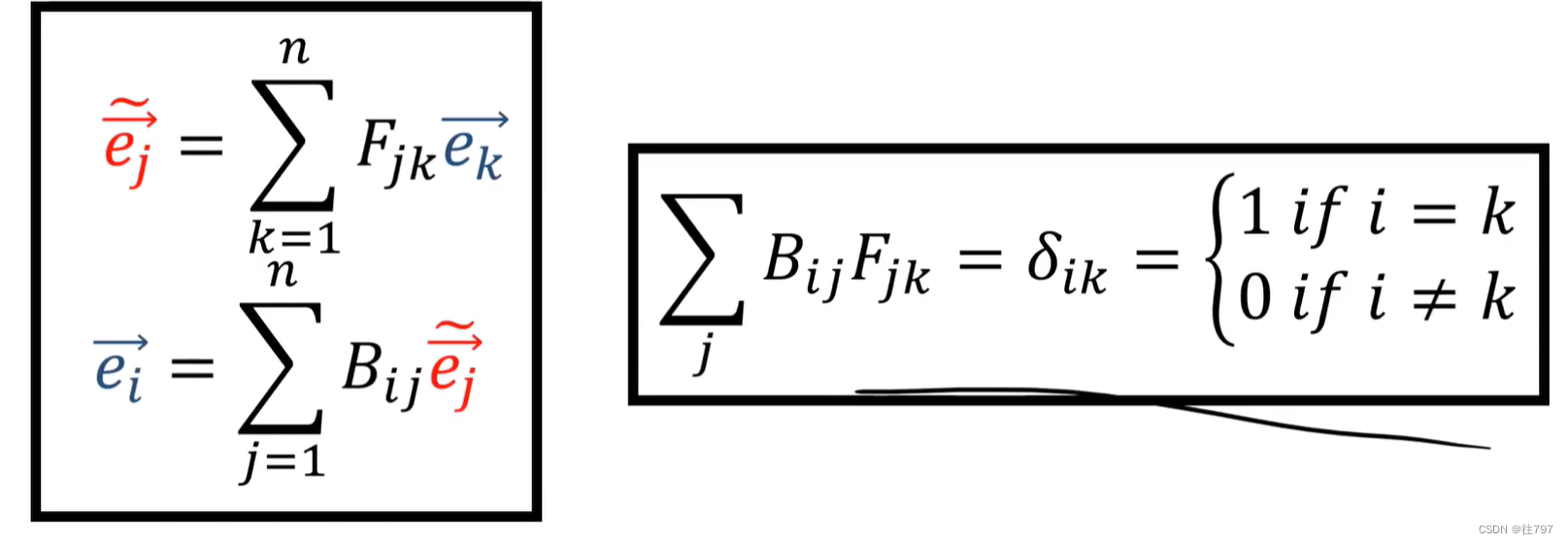transformations专题

usaco 1.2 Transformations（模拟）

我的做法就是一个一个情况枚举出来注意计算公式：（变换后的矩阵记为C）顺时针旋转90°：C[i] [j]=A[n-j-1] [i] （旋转180°和270° 可以多转几个九十度来推）对称：C[i] [n-j-1]=A[i] [j] 代码有点长。。。 /*ID: who jayLANG: C++TASK: transform*/#include<

ResNeXt - Aggregated Residual Transformations for Deep Neural Networks

《Aggregated Residual Transformations for Deep Neural Networks》是Saining Xie等人于2016年公开在arXiv上： https://arxiv.org/pdf/1611.05431.pdf 创新点 1.在传统Resnet基础上采用group convolution，在不增加参数量的前提下，获得更强的representat

Glide 加载刷新闪动，自定义Transformations 必须实现的方法

前言我们使用Glide加载图片，使用自定义对Transformations 转换器的时候，都忽略了定制变换必须实现的方法： updateDiskCacheKeyequals() / hashCode()! 官网这么说明的：为了让内存缓存正常地工作你是否必须实现 equals() 和 hashCode() 方法。很不幸，即使你没有复写这两个方法，BitmapTransformati

Glide-更多图片变换，glide-transformations的使用（六）

Gradle compile 'jp.wasabeef:glide-transformations:3.0.1' 模糊处理 Glide.with(this).load(url).apply(bitmapTransform(new BlurTransformation(25))).into(imageView); 黑白化 Glide.with(this).load(ur

[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-3][Mobius transformations-4]

Conformal Mapping | Möbius Transformation | Complex Analysis #25 摘要：前面我们理解了Mobius transformation 的定义以及一些基本性质，最重要的是了解其confromal map ,以及 inversion 反演的一些特性. 本节依然结合 Petra Bonfe

[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-3][Mobius transformations-3]

前言：参考 Professor Bonfert-Taylor's 《Mobius transformations》，我们重点理解因此莫比乌斯变换是共形映射（ conformal mappinngs ）以及反演特性inversion 目录 mobious transfromation 定义 mobious transfromation 性质 mo

Data augmentation using learned transformations for one-shot medical image segmentation-论文详解

这是一篇CVPR2019的论文，主要是做Magnetic resonance imaging(MRI)医学图像的分割（segmentation)。 MRI 磁共振成像（MRI）是一种用于放射学中的医学成像技术，用于形成人体解剖结构和生理过程的图片。MRI扫描仪使用强磁场，磁场梯度和无线电波来生成体内器官的图像。MRI不涉及X射线或使用电离辐射，这与CT或CAT扫描以及PET扫描不同。磁共振成

Statistical transformations 统计转换

下图显示了钻石数据集中的钻石总数，按切工分组。钻石数据集来自 ggplot2，包含大约 54,000 颗钻石的信息，包括每颗钻石的价格、克拉、颜色、净度和切工。该图表显示，与低质量切割相比，高质量切割的钻石更多。 ggplot(data = diamonds) + geom_bar(mapping = aes(x = cut)) 在 x 轴上，图表显示切工，这是钻石的一个变量。

1.2.2 Transformations

刚开始一看题目，看起来很难的样子，于是就先放过了；等我把其他题做完后，我仔细看了下题目，才发现，这个题目原来这嘛水 …… #include<iostream>#include<fstream>#include<cstring>using namespace std;int n;void Spin( char map[][11], char str[][11], int

OpenGL ES Tutorial for Android – Part III – Transformations

OpenGL ES Tutorial for Android – Part III – Transformations January 1st, 2010 by Per-Erik Bergman — Android, Embedded Last tutorial was about building your polygons. This tutorial is all about trans

文档协作技术——Operational Transformations简单了解

OT是支持协作软件系统的一种广泛使用的技术。 OT通常使用副本文档储存，每个客户端都拥有对文档的副本。客户端在本地副本以无锁非堵塞方式操作，并将改变传递到其他客户端。当客户端收到其他客户端传播的改变之后，通过转换应用更改，从而保证一致性初始文档为"abc"，并存在客户端A、B A发起操作O1=insert[0, “x”]，在位置0插入字符x B发起操作O2=delete[2, “c”

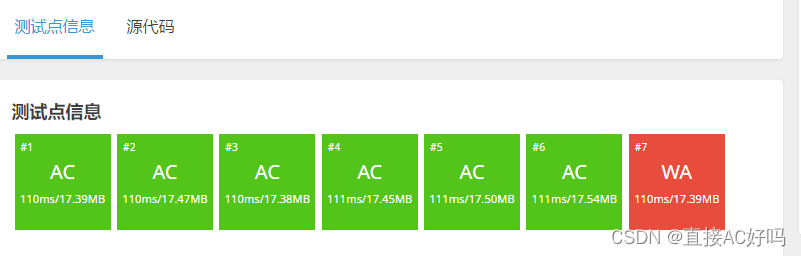
洛谷 P1205 [USACO1.2]方块转换 Transformations

题目描述一块N x N（1<=N<=10）正方形的黑白瓦片的图案要被转换成新的正方形图案。写一个程序来找出将原始图案按照以下列转换方法转换成新图案的最小方式： 1：转90度：图案按顺时针转90度。 2：转180度：图案按顺时针转180度。 3：转270度：图案按顺时针转270度。 4：反射：图案在水平方向翻转（以中央铅垂线为中心形成原图案的镜像）。 5：组合：图案在水平方向翻转，然后

RDD算子——转换操作（Transformations ）【map、flatMap、reduceByKey】

一、map map 算子 # spark-shellsc.parallelize(Seq(1, 2, 3)).map( num => num * 10).collect()# IDEA@Testdef mapTest(): Unit = {// 1. 创建RDDval rdd1 = sc.parallelize(Seq(1, 2, 3))// 2. 执行 map 操作val rdd2 =

方块转换 Transformations（洛谷）（浇浇我）

题目描述一块 n × n n \times n n×n 正方形的黑白瓦片的图案要被转换成新的正方形图案。写一个程序来找出将原始图案按照以下列转换方法转换成新图案的最小方式：转 90 ° 90\degree 90°：图案按顺时针转 90 ° 90\degree 90°。转 180 ° 180\degree 180°：图案按顺时针转 180 ° 180\degree 180°。

方块转换 Transformations（洛谷）（浇浇我）

题目描述一块 n × n n \times n n×n 正方形的黑白瓦片的图案要被转换成新的正方形图案。写一个程序来找出将原始图案按照以下列转换方法转换成新图案的最小方式：转 90 ° 90\degree 90°：图案按顺时针转 90 ° 90\degree 90°。转 180 ° 180\degree 180°：图案按顺时针转 180 ° 180\degree 180°。

（阅读笔记）Oblivious Neural Network Predictions via MiniONN Transformations

不经意神经网络预测动机MINIONN框架本文总结动机云托管模型受到青睐，用户倾向选择云预测（推理）服务；用户数据包含隐私，如何避免隐私泄露；用户-云协同预测轻量化。隐私保护效果：用户对模型未知，服务器对用户数据未知。本文工作：不改变明文下的神经网络模型，实现与之对应的不经意神经网络（采用OT协议）；为神经网络预测的公共函数设计相应的不经意计算协议。单指令

OpenGL学习脚印: 坐标和变换的数学基础(math-coordinates and transformations)

写在前面上一节介绍了向量和矩阵，本节将熟悉坐标、线性变换、仿射变换以及坐标转换等概念和计算方法，这些内容对后续的学习将会有很大帮助。部分内容不是OpenGL编程初学者所必须掌握的，可以在以后需要时再回头来看。这里是对这些知识点的一个总结，旨在对他们有个整体把握，后面具体应用时会使用这些概念。内容尽量以例子形式说明，仅在必要时会给出数学证明。一个主题往往涉及过多内容，对于文中省略的部分，请参

label-preserving transformations

label-preserving transformations,这是一种减少过拟合的方式。也就是在不影响图像标签的前提下，对图片进行变换，以达到数据增强的目的。通过这种方式增大我们的数据集，来减少过拟合。两种数据增强方式： 1第一种数据增强方式包括产生图像变换和水平翻转。从256×256图像上通过随机提取224 × 224的图像块实现了这种方式，然后在这些提取的图像块上进行训练。

2021-03-23转发《ORACLE CBO 的 SQL 自动转换（Cost Based Transformations）之一》

我用#CSDN#这个app发现了有技术含量的博客，小伙伴们求同去《ORACLE CBO 的 SQL 自动转换（Cost Based Transformations）之一》, 一起来围观吧 https://blog.csdn.net/weixin_50513167/article/details/115124637?utm_source=app&app_version=4.5.5

3.Tensors For Beginners- Forward and Backward Transformations

张量在不同坐标系之间来回移动的规则究竟如何。之前说过，张量在坐标系变化下是不变的，故了解如何在坐标系之间来回移动对理解张量很重要。 Forward：旧基到新基 old basis：旧基这是在二维坐标系下的两组基。线性代数中的基：向量空间V中的一组向量若满足： 1）线性无光 2）向量中间V中的任何一个向量都可由该组向量线性表出，则称该组向量为向量空间V的