[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-3][Mobius transformations-4]

本文主要是介绍[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-3][Mobius transformations-4]，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Conformal Mapping | Möbius Transformation | Complex Analysis #25

摘要：

           前面我们理解了Mobius transformation 的定义以及一些基本性质，

最重要的是了解其confromal map ,以及 inversion 反演的一些特性.

          本节 依然结合 Petra Bonfert-Taylor 的《Möbius transformatios》深入

了解一下Mobius transformations，下一节我们重点学习一下《The Riemann Mapping Theorem》

黎曼映射定理

回顾一下Mobisu 变换

目录：

1.     composition  mobius transformation
2.     inversion is  mobius transformation
3.      mobius transformation unique
4.      compositions of Mobius transformations

---

一   composition  mobius transformation

       两个mobius transformation 的复合也是mobius transformation。

       利用这个性质后面会证明其conformal ,共形原理.

       证明：

              写得有误： 

   

---

二 inversion（反演） mobius transformation 也是mobius transformation

    

---

三    mobius transformation unique

     在扩充复平面上有三个不同的点 和 另外三个不同的点 ,
存在唯一的莫比乌斯变换 f:  将映射到,j =1,2,3

       证明：                  

           

                      假设  ,  我们经常利用该性质得到

                  

                 

   例子：

---

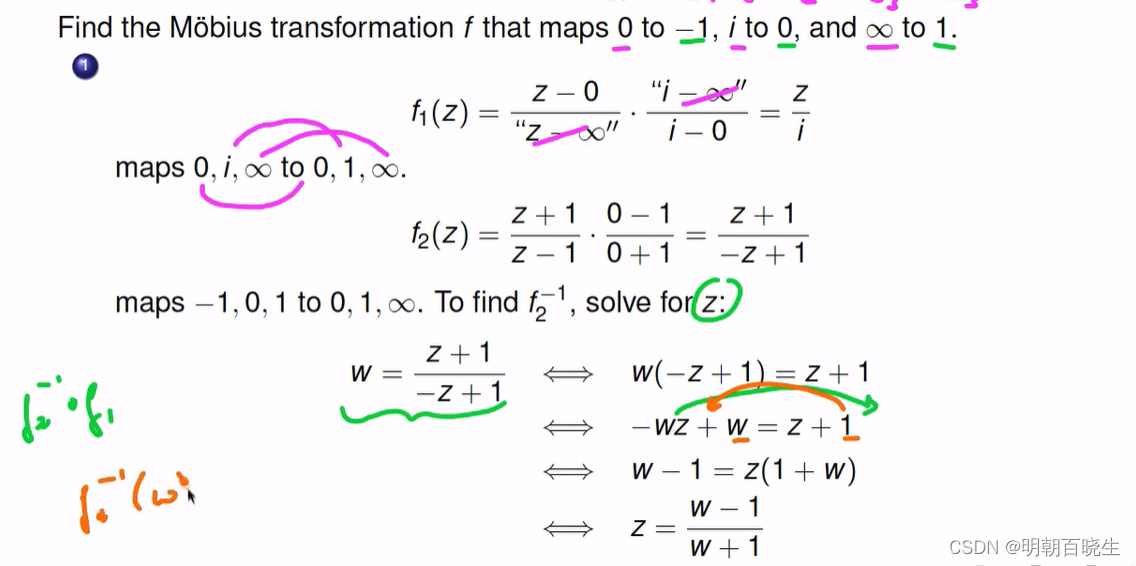
四  compositions of Mobius transformations

设

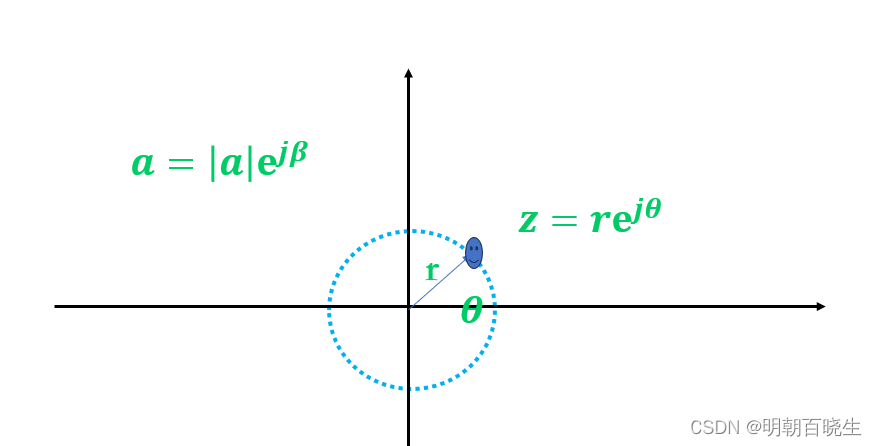
则 Mobius transformation 本质上是由下面三种变换得到

例子 ：

 

参考

Week4Lecture2: Conformal mappings

Week4Lecture4: Möbius transformatios, part II

这篇关于[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-3][Mobius transformations-4]的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---