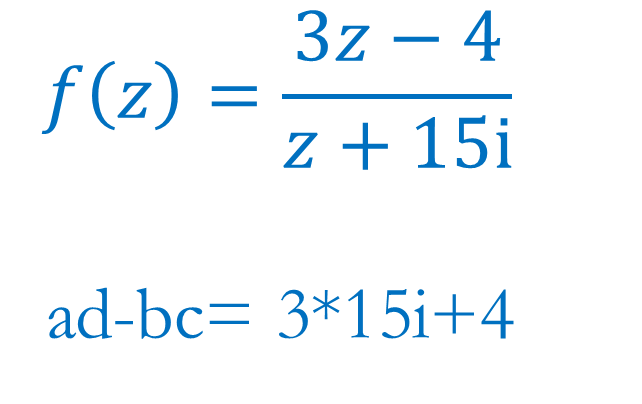[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-3][Mobius transformations-3]

本文主要是介绍[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-3][Mobius transformations-3]，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言：

          参考 Professor Bonfert-Taylor's  《Mobius transformations》，我们重点理解

因此莫比乌斯变换是共形映射（ conformal mappinngs ）以及反演特性inversion 

目录

1.    mobious transfromation 定义
2.    mobious transfromation 性质
3.    mobious transfromation  例子

---

一   mobious transfromation 定义

      mobious 变换有时候也称为分数线性变换(fractional linear transformation)

  例一： Mobius transformation 

         

    满足约束条条件,是mobious transfromation.

 1.1   当

            b,d 可以忽略，则

            

  1.2 当 

             

       我们因此定义

         

1.3   

             

             

因此，我们将 f 是定义在扩充复平面上的映射.

扩充复平面是指在普通的复平面z加入无穷远点构成的集合

    

---

二 Properties of mobious transfromation.

   

     1.1 f(z) 是非常数（non-constant ）

          证明：

           先求导,导数不为0,所以f(z)不能是常数

         

            对于任意z ，,因为导数不为0 ，所以f(z)也不能为常数

      

    1.2  非唯一性(not uniquely)

           

     如果分子分母同乘以一个constant k我们发现结果不变,所以对于给定的变换f(z) a,b,c,d并不是唯一的.

       

   1.3 one to one  一对一映射

           

          后面通过这点去理解 images and pre-images of infinity 无穷远的像和原像一一对应关系。

---

三  放射变换性质 （affine transformation ）

        设 c= 0,d=1, 则 ,

        因为 Mobius 变换

        

           做旋转,膨胀,平移等操作（rotation  dilation  translation）

         i.e  b=0 时

               相当于对原图像做旋转和膨胀（rotation&dilation）

         i.e  a=1 时

              对原图像做平移（translation）

         

        通过极坐标可以很容易查看出来。

            

---

四  反演 变换（inveration）性质

     4.1 定义

        当  这就是反演（inversion）

      

     4.2 保圆性例1： 

        设  则 

4.2   不过圆心的circle 反演（Inversion）： 

     设圆通过mobius 变换后的图像是什么呢？

      设 是一个半径为1的圆，中心点在3.

    那经过Mobius  Inversion 变换后的图像  是什么呢？

     根据Inversion 定义：

                                         

                                           

    

   几何效果如下

4.3  过圆心的circle 反演（Inversion）

        是半径为1的圆，中心点在1，那么f(k)是什么？

几何意义：

   过圆心的圆通过Mobius 变换后得到一个的直线

  我们总结一下映射关系

4.4： 直线的反演（Inversion）

        设直线  

          则

                      

                                

参考：

https://www.youtube.com/watch?v=b6QJ6pb30q8

https://www.youtube.com/watch?v=u2e0Dc1wV2k&t=233s

默比乌斯变换_百度百科

这篇关于[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-3][Mobius transformations-3]的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---