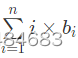ntt专题
ZOJ 3904 Birthday Gift【NTT】
首先,我们知道的是, num1+num2=N num_1+num_2=N,其中 num1 num_1是Alice的盒子数, num2 num_2是Bob的盒子数。 那么 ans[N]=∑Alice(num1)×Bob(N−num1) ans[N]=\sum Alice(num_1)\times Bob(N-num1),明显是FFT的卷积形式。 接下来分析 Alice(num1) Alice(n
Cells(2021牛客暑期多校训练营9 C,LGV引理 + 范德蒙德行列式 + NTT)
一、题目链接 Cells 二、题目大意 在一个二维平面内,有 n n n 个起点 ( 0 , a i ) (0, a_i) (0,ai) 要走到对应的终点 ( i , 0 ) (i, 0) (i,0),每次可以向下走或向左走,问不相交路径组的方案数. 1 ≤ n ≤ 5 × 1 0 5 , 0 ≤ a i ≤ 1 0 6 , a i < a i + 1 1 \leq n \leq
2021牛客多校1 H hashfunction FTT/NTT,数论
H 题意 n个数哈希,策略是直接模一个数。求最小的不冲突模数 范围0-50w H 思路 冲突时当且仅当|ai-aj|%m=0 换句话说,m不能是任何一对aiaj的约数,数的范围不大,如果我们能知道所有|ai-aj|,那么我们枚举m,判断下他每一个倍数有没有出现过,就可以判断m是否可以做答案。这个复杂度是调和级数,nlogn级别的。 下面问题在于我们如何知道所有的ai-aj。这里需要一个前置知
NTT Research与东京大学国际神经智能研究中心开展神经计算联合研究
(图片来源:网络) 神经网络科学对于相干量子计算研发有着重要的价值。 在NTT Research 2020峰会上,东京大学国际神经智能研究中心(IRCN)Timothee Leleu博士发表题为《Neuromorphic in Silico Simulator for the CIM》演讲时讲到,利用神经网络原理能够提高CIM(Coherent Ising Machine,相
快速数论变换NTT学习笔记
什么是NTT? 数论变换(number-theoretic transform, NTT)是离散傅里叶变换(DFT)在数论基础上的实现。 NTT是一种计算卷积的快速算法,FFT也是其中一种。 但是FFT具有一些实现上的缺点,举例来说,向量必须乘上复数系数的矩阵进行处理,而且每个复数系数的实部和虚部是一个正弦及余弦函数,因此大部分的系数都是浮点数,也就是说,必须做浮点复数运算,计算量会比较大,并
分治NTT(洛谷P4721)
题目路径:P4721 【模板】分治 FFT - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 思路: 如果用NTT一个一个求时间复杂度是O(n^2)。 可以发现,i<j,f[i]会对f[j]有贡献,而f[j]对f[i]没有贡献,考虑分治。 对于区间(l,r),当我们算出f[l]-f[mid](mid=(l+r)>>1),我们可以算出(l,mid)对后边区间贡献,再算(mid
牛客国庆集训派对Day4-E-乒乓球(NTT)
链接:https://www.nowcoder.com/acm/contest/204/E 来源:牛客网 题目描述 小 Bo 是某省乒乓球名列前茅的选手,现在他有 n 颗乒乓球一字排开,第 i 颗乒乓球的权值为 wi 每次他会随机从现有的乒乓球中等概率选一颗拿走,然后得到的收益是这颗球左边第一个乒乓球和右边第一个乒乓球的权值的乘积,如果左边没有乒乓球或者右边没有乒乓球,则收益为 0,这个过
NTT+分治FFT--P4091 [HEOI2016/TJOI2016]求和
传送门 这道题很妙啊 首先看题目中的式子,令新的 f ( n ) = ∑ i = 0 n S ( n , i ) × 2 i × ( i ! ) f(n)=\sum_{i=0}^nS(n,i)\times 2^i\times (i!) f(n)=∑i=0nS(n,i)×2i×(i!),如果能快速求出这个式子的值,那么 a n s = ∑ i = 0 n f ( i ) ans=\sum_{i
NTT Communications和Arkadin荣获Frost Sullivan亚太区信息与通信技术奖
东京--(美国商业资讯)--NTT集团 (TOKYO:9432)旗下信息和通信技术解决方案公司NTT Communications Corporation (NTT Com)和NTT Communications旗下公司、云统一通信和协作服务市场领导者Arkadin今天宣布,两家公司双双荣获2018年Frost & Sullivan亚太区信息与通信技术奖(Frost & Sullivan 2018
NTT计划成立NTT Global Sourcing, Inc.
东京--(美国商业资讯)--日本电报电话公司(NTT;总部:东京都千代田区;总裁兼首席执行官:Jun Sawada)(TOKYO:9432)将于2018年11月(计划时间)成立一家专门从事采购的新公司,通过汇集每家集团公司的采购量,与全球供应商等进行集中价格谈判和签订全面协议。新公司将隶属于NTT, Inc.,计划在截至2019年3月31日财年的第三季度建立。 1.目的和角色 NTT将在美
NTT Communications在2019年世界通信奖中被评为年度最佳运营商
东京--(美国商业资讯)--NTT集团(TOKYO: 9432)旗下的信息通信技术(ICT)解决方案业务分支NTT Communications Corporation (NTT Com)今天宣布,该公司于10月30日在伦敦举行的2019年世界通信奖(World Communication Awards 2019)颁奖仪式上被评为“年度最佳运营商”(Operator of the Year)。
NTT:签订国际热核聚变实验堆(ITER)合作协议
东京--(美国商业资讯)--NTT Corporation(NTT,总裁兼首席执行官:Jun Sawada)与国际热核聚变实验堆组织(ITER Organization)签订了一项ITER项目合作协议。 ITER项目的目标是建造世界第一个实验性氢聚变反应堆。通过为该项目提供支持,NTT将加快“创新的环境和能源技术的发展”,并为减少客户、公司和社会的环境影响做出贡献。 此新闻稿包含多媒体内容。完整
拉斯维加斯市将与NTT合作加速推进其智慧城市项目
拉斯维加斯--(美国商业资讯)--拉斯维加斯市和NTT Corporation (NTT)今天宣布,该市的Accelerate Smart项目新增两处新地点——社区疗愈花园以及位于南大街和东圣路易斯大街的拉斯维加斯大道的一部分。在这项合作中,NTT和拉斯维加斯市还计划今年夏天将智慧城市项目进一步扩展到Bob Baskin公园、Rotary公园、Stupak公园和Ethel Pearson公园,随后
NTT:首席执行官调查显示,员工和环保对企业日益重要
东京--(美国商业资讯)--受全球技术和业务解决方案提供商NTT委托,WSJ Intelligence进行了一项最新国际首席执行官调查。调查聚焦于企业在帮助实现社会目标方面的作用。 WSJ Intelligence此次调查对象包括大型公司的351名首席执行官,这些公司代表15个国家的十大重要行业。调查旨在了解这些高管对一些问题的看法,如有关他们所在企业在社会中的作用、企业的社会影响力策略、所
NTT发布通用光量子计算机关键部件:一种新型光源
(图片来源:网络) 近日,由NTT、东京大学、RIKEN(日本理化研究所)组成的研究团队宣布了他们在光量子计算机研发关键步骤上的重大进展:研制出新型光纤耦合量子光源(压缩光源),这标志着向容错的大规模通用量子计算机的落地迈出了关键一步。 当前量子计算机的研发工作在全世界内火热进行。在众多的量子计算机设计路线中,光量子技术路线的优势正在凸显。 例如,光量子计算机能够在室温环境下
NTTRU:兼容 NTT 算法的 NTRU-based KEM 方案
参考文献: [CT65] Cooley J W, Tukey J W. An algorithm for the machine calculation of complex Fourier series[J]. Mathematics of computation, 1965, 19(90): 297-301.[Mont85] Montgomery P L. Modular multiplic
2021icpc澳门 E-Pass the Ball!(NTT)
2021icpc澳门 E-Pass the Ball! 题意 一开始有n个小朋友1-n,手上球的编号为1-n,给一个数组a,每轮第i个小朋友会把球传给ai。有q次询问,每次询问轮数k,第k轮时每个小朋友手上的球为bi,问是多少。(n<=1e5,q<=1e5,k<=1e9) 思路 首先很清楚的就能知道这个传球的顺序就是一个置换群,把这个置换群分解后单独去考虑每个独立的群就行,简单的说就是把这
无限手套 分治 + NTT + 生成函数
无限手套 solution ∏ k = 0 ∞ a i x i 2 + b i x i + 1 \prod\limits_{k=0}^{∞}a_ix_i^2+b_ix_i+1 k=0∏∞aixi2+bixi+1 考 虑 生 成 函 数 : 考虑生成函数: 考虑生成函数: = > ∑ k = 0 ∞ a i k 2 x k + b i x i x k + x k =>\sum