2021icpc澳门 E-Pass the Ball!（NTT）

2021icpc澳门 E-Pass the Ball!

题意

一开始有n个小朋友1-n，手上球的编号为1-n，给一个数组a，每轮第i个小朋友会把球传给ai。有q次询问，每次询问轮数k，第k轮时每个小朋友手上的球为bi，问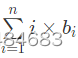是多少。(n<=1e5,q<=1e5,k<=1e9)

思路

首先很清楚的就能知道这个传球的顺序就是一个置换群，把这个置换群分解后单独去考虑每个独立的群就行，简单的说就是把这数组中环的数目分解出来。
然后在对每个环去考虑，显然一次是o(N)的，设len为当前数i所在环的长度那么(k-1+i)%len即为当前轮数该数的值在暴力for一遍求答案就行。但是题目中有q次询问，这样做就不行了，这里我们想如何能快速的处理出每个循环节内每一轮的答案，这里可以先设一个生成函数f(x)=a1 + a2x ^ 2 + a3x ^ 2 + … +akx ^ (k-1)，其中k为当前环内的元素数量，这里我们发现把f(x)里面每一项的系数翻转过来与自身卷积后所得到的每一项的系数和每轮的答案有一定的关系，其中ak为第0轮的答案，而ak-1+a1为第一轮的答案后面类似这个在纸上面画画就能知道。这样我们就能$O(n\ast logn)$的卷出一个环内的答案了，然后合并答案的话我们发现一共环可以有n个而q次询问，这样n*q=1e10了这肯定是不允许了，观察一下可以发现每个长度相同的环他的变换的同步的所以可以合并，而不同长度的环的数量显然只能有根号n级别个，那么合并就只需要$O(q\ast \sqrt{n})$,然后就能解出这道题了。

总时间复杂度为$O(q\ast \sqrt{n})+O(n\ast logn)$

提示点：因为要卷积很多次所以每次要清空数组，还有这题会报long long,FFT好像精度卡的好的话可以过，NTT的写法的话要找到一个1e18左右的模数可以查原根表或者写个暴力判原根。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 500007;
const ll p = 180143985094819841, G = 6;
int x,k;
bool vis[N];
ll p1[N],p2[N],xi[N];
vector<ll>ans[101000];
int n1,q;
ll limit = 1;//
ll L;//二进制的位数
ll RR[N];
ll a[N], b[N];ll qpow(ll a, ll b)
{ll res = 1;while(b) {if(b & 1) res =(__int128_t) res * a % p;a = (__int128_t)a * a % p;b >>= 1;}return res % p;
}ll inv(ll x) {return qpow(x, p - 2);}void NTT(ll *A, int type)
{for(int i = 0; i < limit; ++ i)if(i < RR[i])swap(A[i], A[RR[i]]);for(int mid = 1; mid < limit; mid <<= 1) {//原根代替单位根ll wn = qpow(G, (p - 1) / (mid * 2));if(type == -1) wn = qpow(wn, p - 2);for(int len = mid << 1, pos = 0; pos < limit; pos += len) {ll w = 1;for(int k = 0; k < mid; ++ k, w = ((__int128_t)w * wn) % p) {ll x = A[pos + k], y =(__int128_t) w * A[pos + mid + k] % p;A[pos + k] = ((__int128_t)x + y) % p;A[pos + k + mid] = ((__int128_t)x - y + p) % p;}}}if(type == -1) {ll limit_inv = inv(limit);//N的逆元（N是limit, 指的是2的整数幂）for(ll i = 0; i < limit; ++ i)A[i] = ((__int128_t)A[i] * limit_inv) % p;//NTT还是要除以n的，但是这里把除换成逆元了，inv就是n在模p意义下的逆元}
}
//多项式乘法
void poly_mul(ll *a, ll *b, int deg)
{for(limit = 1, L = 0; limit <= deg; limit <<= 1) L ++ ;for(ll i = 0; i < limit; ++ i) {RR[i] = (RR[i >> 1] >> 1) | ((i & 1) << (L - 1));}NTT(a, 1);NTT(b, 1);for(ll i = 0; i < limit; ++ i) a[i] = (__int128_t)a[i] * b[i] % p;NTT(a, -1);
}
int A[N];
int main(){scanf("%d%d",&n1,&q);for(int i=1;i<=n1;i++){scanf("%d",&A[i]);}for(int i=1;i<=n1;i++){if(!vis[i]){int noww=0;a[noww++]=i;vis[i]=true;for(int j=A[i];!vis[j];j=A[j]){a[noww++]=j;vis[j]=true;}for(int j=noww;j<=4*noww;j++){a[j]=b[j]=0;}for(int j=noww-1;j>=0;j--){b[j]=a[noww-1-j];}poly_mul(a, b, 2*noww-2);for(int j=0;j<noww;j++){p1[j]=a[j];}for(int j=0;j<noww-1;j++){a[j]=a[j]+p1[noww-2-j];}if (!ans[noww].size()) ans[noww].resize(noww);for(int j=0;j<noww;j++){ans[noww][j]+=a[(noww+j-1)%noww];}}}vector<int> si;for(int i=1;i<=n1;i++){if(ans[i].size()) si.push_back(i);}for(int i=1;i<=q;i++){int k;ll Ans=0;scanf("%d",&k);for(int j: si){Ans=Ans+ans[j][k%j];}printf("%lld\n",Ans);}return 0;
}