lct专题
【HDU】5333 Undirected Graph【LCT+BIT】
传送门:【HDU】5333 Undirected Graph my code: my~~code: #pragma comment(linker, "/STACK:1024000000")#include <stdio.h>#include <string.h>#include <map>#include <algorithm>using namespace std ;typed
P4842 城市旅行(拆贡献 + LCT)
https://www.luogu.com.cn/problem/P4842 发现题目就是要维护一个LCT,然后我们只要把pushup写成功了就行。 那我们现在就不管LCT了,就单纯想用一棵二叉查找树怎么维护。分母是好搞的,分子我们要想点办法。 考虑右子树对左子树的贡献,我们假设处理出一个 L [ k ] L[k] L[k] 表示左子树中每个值乘以左边界的可选数量,我们现在再乘上右子树的大
AMEYA360代理 | 村田电子去寄生电感降噪元件(LCT)特点和规格
株式会社村田制作所(以下简称“村田”)开发了行业首款(1)利用负互感(2)、能对从数MHz到1GHz的谐波(3)范围内电源噪声进行抑制的去寄生电感降噪元件“LXLC21系列”(以下简称“本产品”)。只需将1件本产品连接至电源电路中的电容器,即可消除与本产品连接的电容器的ESL(4),并提高电容器的噪声消除性能。由此用比以前更少数量的电容器就可以抑制噪声,从而助力实现电子设备的小型化和高功能化。L
72【leetcode】经典算法- Lowest Common Ancestor of a Binary Search Tree(lct of bst)
题目描述: 一个二叉搜索树,给定两个节点a,b,求最小的公共祖先 _______6______/ \___2__ ___8__/ \ / \0 _4 7 9/ \3 5 例如: 2,8 ---->6 2,4----->2 原文描述: Given a b
bzoj 2959: 长跑(LCT + 并查集 维护边双通)
对图跑一遍 tarjan,对边双通缩点得到一棵树,答案就是树上两点路径之间的点权和。 因为过程中有加边操作,考虑用 LCT 来维护边双通。 在加边时,若加入这条边没有形成环,则直接加边。若形成了环,则需要在 LCT 上进行暴力缩点。 考虑每个节点维护一个 b e l [ u ] bel[u] bel[u] 表示每个点所在的边双通, LCT 辅助树上只维护边双通的代表点,其它的点不维
(Luogu) P3950 部落冲突 (LCT || 树链剖分)
传送门 解:LCT解决这个就非常直接了,直接断边连边,检查一下连通性就行了。 #include<bits/stdc++.h>#define il inline#define pb push_back#define ms(_data,v) memset(_data,v,sizeof(_data))#define SZ(a) int((a).size())#define ls ch[x]
LCT动态树-基础模板(luogu P3690)
学习来自 P3690 【模板】Link Cut Tree (动态树) 给定n个点以及每个点的权值,要你处理接下来的m个操作。操作有4种。操作从0到3编号。点从1到n编号。 0:后接两个整数(x,y),代表询问从x到y的路径上的点的权值的xor和。保证x到y是联通的。 1:后接两个整数(x,y),代表连接x到y,若x到y已经联通则无需连接。 2:后接两个整数(x,y),代表删除边(x,y)
Long-term Correlation Tracking LCT目标跟踪算法原理详解(个人学习笔记)
目录 1. 算法总览2. 算法详解2.1. 基础相关滤波跟踪2.2. 各模块详解2.2.1. 相关跟踪2.2.2. 在线检测器 3. 算法实现3.1. 算法步骤3.2. 实现细节 4. 相关讨论&总结 1. 算法总览 LCT的总体流程如上图所示,其思想为:将长时跟踪(long-term tracking)分解为对运动目标的平移(translation)估计和尺度(scale
BZOJ3669 膜法森林 - LCT
Solution 非常妙的排序啊。。。 仔细想想好像确实能够找出最优解QUQ 先对第一关键字排序, 在$LCT$ 维护第二关键字的最大值 所在的边。 添边时如果$u, v$ 不连通 就直接加边。 如果连通 并且路径上的最大值 大于 当前边 的 第二关键字, 那么可以换掉。 如果 $1$ 和 $N$ 连通 就 更新答案。 这样就可以保证 在 所有路径上的边 第一关键字 小于等于 当前边 的第
【bzoj3514】【Codechef MARCH14 GERALD07加强版】【lct+主席树】
Description N个点M条边的无向图,询问保留图中编号在[l,r]的边的时候图中的联通块个数。 Input 第一行四个整数N、M、K、type,代表点数、边数、询问数以及询问是否加密。 接下来M行,代表图中的每条边。 接下来K行,每行两个整数L、R代表一组询问。对于type=0的测试点,读入的L和R即为询问的L、R;对于type=1的测试点,每组询问的L、R应为L xor
差值最小生成树[LCT]
传送门 将边按边权从小到大排序; 如果插入的两个点在一棵树上,就找他们路径上权值最小的那条边并删除,然后在新加一条边 否则直接加就好了 路径需要以点的形式插入到LCT,第i跳路径对于i+n号节点,Link(x,y) 就Link(x,i+n),Link(i+n,y) 就好了 维护一下最小值 #include<bits/stdc++.h>#define N 1000005#de
【51nod1600】Simple KMP(SAM)(LCT)(差分)
题意: 对于一个字符串 ∣ S ∣ |S| ∣S∣,我们定义 f a i l [ i ] fail[i] fail[i],表示最大的 x 使得 S [ 1.. x ] = S [ i − x + 1.. i ] S[1..x]=S[i-x+1..i] S[1..x]=S[i−x+1..i],满足 ( x < i ) (x<i) (x<i) 显然对于一个字符串,如果我们将每个 0 < =
【LCT】历史(P4338)
正题 P4338 题目大意 有一棵树,告诉你每个点access的次数(带修改),问实链切换的最多次数 解题思路 先考虑离线的做法: 对于点 x,其不同儿子的子树access会使实链切换(对于点 x access 同理),每次都让不同儿子的子树 access,显然可以让答案最大化 但答案不一定是 s z x − 1 sz_x-1 szx−1(最后无法切换),因为如果存在一个
LCT模板 LCT题型大荟萃
以HDU4010为例,写了LCT相关的一些题目的做法 #include<stdio.h>#include<iostream>#include<string.h>#include<string>#include<ctype.h>#include<math.h>#include<set>#include<map>#include<vector>#include<queue>#
[UOJ 3]【NOI2014】魔法森林:LCT
点击这里查看原题 将所有路径按a升序排序,用LCT维护路径上最大的b,将边权化为点权,如果加入一条边x,其两端点分别为u,v,那么将u与i+x连边,v与i+x连边。 如果(u,v)路径最大的b值大于当前边的b,那么删去b最大的边。 注意:access操作中必须pushup,因为这个调了好久 /*User:SmallLanguage:C++Problem No.:3*/#inclu
「NOI2014」 魔法森林 - 动态树LCT
题目描述 为了得到书法大家的真传,小E同学下定决心去拜访住在魔法森林中的隐士。魔法森林可以被看成一个包含个 N N N节点 M M M条边的无向图,节点标号为 1 ⋯ N 1\cdots N 1⋯N,边标号为 1 ⋯ M 1\cdots M 1⋯M。初始时小E同学在号节点 1 1 1,隐士则住在号节点 N N N。小E需要通过这一片魔法森林,才能够拜访到隐士。 魔法森林中居住了一些妖怪。每当有
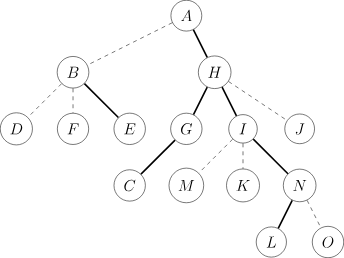
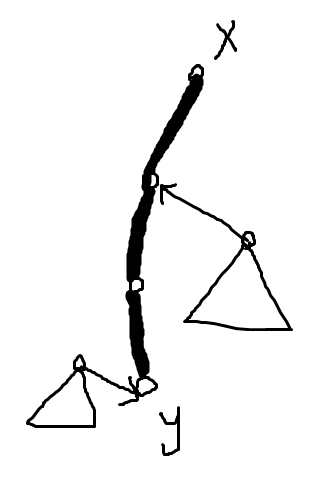
LCT(link cut tree) 详细图解与应用
樱雪喵用时 3days 做了 ybtoj 的 3 道例题,真是太有效率了!!1 为了避免自己没学明白就瞎写东西误人子弟,这篇 Blog 拖到了现在。 图片基本沿用 OIwiki,原文跳步骤(主要是 access 部分)的就自己补画了一些。 不过反正也没啥人看? 前置知识 Splay 欢迎阅读 Splay 详细图解 & 轻量级代码实现。 其实 LCT 对 Splay 的要求主要体现在维护序列
HDU 5967 小R与手机 (LCT)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5967 题解:通过LCT来维护基环内向树 由于这是一个有向图,所以所有树都有根 对于可能形成环的边,我们可以发现一定是从树的根连出去的,我们只需要维护LCT的时候标记这个树根有没有连接到内部的边,在每次cut操作的时候判断能不能把这条边加进来,如果可以就进行link操作,注意可能
[BZOJ3669][Noi2014]魔法森林 LCT
这道题有两个权值 我们把所有边按权值a排序 剩下的边都看成点放进一个LCT中 维护每一节点的最大权值点的位置 枚举所有的边 如果u, v连通 则删去最大的边 加入这条边 否则直接加入这条边 当发现1和n连通的时候更新答案 开数组的时候把val 和 MAX开成bool也是醉了orz #include<cstdio> #include<algorithm> #include<cstr
[HDU4010]Query on The Trees LCT
找个要打懒标记的裸题刷一刷Orz 然后数组没清干净结果RE了好久 #include<cstdio>#include<algorithm>#include<cstring>#include<iostream>#include<queue>#define SF scanf#define PF printfusing namespace std;typedef long long
LCT(Link-Cut Tree)详解(蒟蒻自留地)
最近自学了LCT,发现网上的资料讲解不是很全面,像我这样的蒟蒻一时半会根本理解不了。我弄了很久总算是理解了LCT,打算总结一下LCT的基本操作,还请诸位神牛来找找茬。 如果你还没有接触过LCT,你可以先看一看这里: (看不懂没关系,先留个大概的印像)http://www.cnblogs.com/BLADEVIL/p/3510997.html 看完之后我们知道,LCT和静态的树链剖分很
LCT(Link Cut Tree)学习小记
动态树(Dynamic Tree) 之前我一直以为这是一种数据结构,最近才明白这是指一类问题。 在学习LCT之前首先要学习树链剖分。 树链剖分就是将一棵树划分成若干条链,用数据结构去维护每条链,复杂度为O(logN)。 树链剖分针对的是树的形状不会变的树,但是如果树的形状是会变的(即要支持将树分离、合并的操作),就需要用到LCT(Link Cut Tree)了。 LCT大概思路就是用sp
[bzoj3282][LCT]Tree
Description 给定N个点以及每个点的权值,要你处理接下来的M个操作。 操作有4种。操作从0到3编号。点从1到N编号。 0:后接两个整数(x,y),代表询问从x到y的路径上的点的权值的xor和。 保证x到y是联通的。 1:后接两个整数(x,y),代表连接x到y,若x到Y已经联通则无需连接。 2:后接两个整数(x,y),代表删除边(x,y),不保证边(x,y)存在。 3:后接两个整
[bzoj2594][LCT]水管局长数据加强版
Description SC省MY市有着庞大的地下水管网络,嘟嘟是MY市的水管局长(就是管水管的啦),嘟嘟作为水管局长的工作就是:每天供水公司可能要将一定量的水从x处送往y处,嘟嘟需要为供水公司找到一条从A至B的水管的路径,接着通过信息化的控制中心通知路径上的水管进入准备送水状态,等到路径上每一条水管都准备好了,供水公司就可以开始送水了。嘟嘟一次只能处理一项送水任务,等到当前的送水任务完成了,