dinic专题
POJ训练计划1459_Power Network(网络流最大流/Dinic)
解题报告 这题建模实在是好建,,,好贱,,, 给前向星给跪了,纯dinic的前向星竟然TLE,sad,,,回头看看优化,,, 矩阵跑过了,2A,sad,,, /*************************************************************************> File Name: PowerN.cpp> Author: _nplus>
关于Dinic算法的几点讨论
基本概念 Dinic算法是经典的网络最大流算法,该算法由在EK算法的基础上增加"分层"这一概念得到。算法复杂度为,求解二分图最大匹配的时间复杂度为 算法过程 分层操作: 进行一次BFS。在BFS的过程中不断对未访问过的结点进行分层。在分层的过程中,使用一个队列保存需要进行分层的点集,并用一个d[N]数组保存每个结点所在的层数。 算法主体(Dinic): 在算法的主体过程中,我们只从层数
网络最大流增广路模板(EK Dinic)
EK算法: int fir[maxn];int u[maxm],v[maxm],cap[maxm],flow[maxm],nex[maxm];int e_max;int p[maxn],q[maxn],d[maxn];void add_edge(int _u,int _v,int _w){int e;e=e_max++;u[e]=_u;v[e]=_v;cap[e]=_w;nex[e]
最大流的Dinic算法
基于Ford-Fulkerson方法的原始的DFS算法效率是比较低的,因此针对如何尽快的扩流存在一系列的改进算法,例如Dinic算法。Dinic算法的基本思路是:在一次搜索中,在层次间进行扩流,而不是仅对一条路径进行扩流。所谓层次,就是指各节点距离起点的路径长度。当然,每个节点的层次随着残量的变化而变化。 Dinic算法的基本流程是: 1、根据残量网络计算层次图,使用BFS; 2、
网络流模板 Dinic+ISAP
dinic递归版,堆栈溢出可以手动扩栈,改成非递归版本,或者改用效率更高的ISAP。 struct Edge{int from, to, cap, flow;Edge(){}Edge(int from, int to, int cap, int flow) : from(from), to(to), cap(cap), flow(flow){}};int n, m, s, t;ve
POJ 3308 Paratroopers(最小割+Dinic)
题目链接:http://poj.org/problem?id=3308 题意:外星人来攻打地球了。。。外星人派了一些伞兵来攻占地球的兵工场,兵工厂是一个矩形网格,伞兵会降落在兵工厂的某个位置。地球人有激光武器,可以杀死一行或者一列的所有敌人。但是每个激光武器安置在每行每列的费用都是不同的。伞兵很厉害只要一个就可以消灭兵工厂,所以,现在要部署一套激光系统使得伞兵一降落就可以消灭所有敌人。并且要求费
POJ 1459 Power Network(Dinic邻接表+当前弧优化)
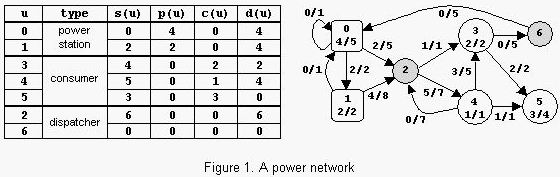
题目链接:http://poj.org/problem?id=1459 题意:一个电网包含一些结点(电站、消费者、调度站),这些结点通过电线连接。每个结点u 可能被供给s(u)的电能,s(u)≥0;同时也可能产生p(u)的电能,0≤p(u)≤pmax(u);站点u 还有可能消费c(u)电能,0≤c(u)≤min( s(u), cmax(u) );可能传输d(u)的电能,d(u) = s(u) +
poj3281 DINIC
如题:http://poj.org/problem?id=3281 初学最大流. 这题重要的是图的构建。源点-》食物-》牛-》牛-》饮料-》汇点。0是源点,1-f食物,f+1-f+1+n食物到牛,f+1+n-f+1+2*n牛到牛,f+1+2*n-f+1+2*n+d牛到饮料,f+1+2*n+d+1最终汇点。 按照上面建图,用DINIC算法求最大流
POJ 2987 Firing (最大权闭合子图Dinic)
题意:公司打算裁员,裁掉某些员工可以获得正收益,而裁掉某些员工会遭受损失。并且员工之间往往存在一定的关系,当某个员工被裁掉之后,在他的关系之下的所有员工都必须被裁掉。现在要求如何裁员才能获得最大收益。 题解:s->正权, 负权->t。 ans = 正权和 - maxflow, 或者 ans = 正权和 - 没有被裁的正权和 - abs(被裁的负权和) ( 正边权进入最小割表示该人没被炒,非正边权
POJ 1149 PIGS (最大流Dinic)
题意:话说一个猪圈管理员,他本身没有猪圈的钥匙。每天会有许多顾客来买猪,这些顾客自己带着某些猪圈的钥匙。每当一个顾客来买猪,这些打开的猪圈里的猪可以随意流动,买完猪之后打开的猪圈全部关闭。现在已知每个猪圈里猪的的数量,每一名顾客拥有的钥匙以及他想购买的猪的数量。求管理员可以卖出的最大数量。 题解:构图是难点在于猪的流动。我是这样想的,假设顾客A可以打开了猪圈1,3,5,他需要购买numA头猪,由
POJ 3281(dinic)
题目链接:http://poj.org/problem?id=3281 题目大意:n头牛,f种食物,d种饮料,然后给出每头牛想吃的食物和饮料,问如果每只牛选一个自己喜欢的食物和饮料,而且每个食物和饮料只能被选一次,问最多能让多少头牛满意 题目思路:这道题有两个限制条件:1、每种食物和饮料只能被选一次。2、每头牛只能选一个喜欢的食物和一个喜欢的饮料。考虑网络流建边。我们把整张图分成三
P3376 【模板】网络最大流(dinic模板)
因为牛客第一场,被迫学习网络流。 代码是《进阶指南》上的模板代码 #include<iostream>#include<cstdio>#include<cstring>#include<algorithm>#include<vector>#include<queue>using namespace std;typedef long long ll;const int inf =
2018年长沙理工大学第十三届程序设计竞赛 K. zzq的离散数学教室2(dilworth定理+有向图可相交路径覆盖 dinic版)
题目 在这个题目中,集合中有n个元素,编号从1到n。它们之间共有m对偏序关系,每一对偏序关系的表示形式为以空格分开的两个编号:x y。含义是x和y之间有关系≤。(这里的≤不是传统意义上的小于等于,可以理解为从y到x的一条有向边),记做:x≤y。同时这些关系也具有传递性,例如,如果x≤y并且y≤z,那么可以得到x≤z。数据保证不会出现同时有x≤y,y≤z,z≤x的情况。 现在我们的问题是,要你从
Atcoder TUPC 2023(東北大学プログラミングコンテスト 2023)P. Sub Brackets(dinic 二分图最大独立集)
题目 长为n(n<=500)的尚未确定的括号串,m(m<=500)个限制条件 第i个限制条件形如区间[li,ri],保证区间长度为偶数, 定下来括号串,满足最多的限制数,使得每个限制对应的区间是一个合法的括号串 输出能满足的最多的限制数 思路来源 官方题解 题解 不合法的情况: li和lj奇偶性不同,li<lj<=ri<rj 考虑把(看成+1,)看成-1,x[i]为括号串的前缀
网络流算法集合 EK dinic 最小费用最大流 (Dijkstra实现)
终于快把网络流的模板写完了,先贴几个,存边用前向星实现,既保证了速度又免去了写链表的麻烦,代码绝对是你能找到的代码中最精简的 //EK#include<stdio.h>#include<iostream>using namespace std;#include<memory.h>#define MAXN 300#define MAXFLOW 2000000000int n,s,t,m,flow[
菜鸟观点---图论之Dinic最大流算法
菜鸟观点----浅谈图论网络流之Dinic算法 欢迎各位读者关注此ID! 今天的头版先给真正的勇士 国家有国家的事情和处理方式,作为我们,能帮助的最多的就是干好自己的本职工作了。 开始正文 Hello大家!我是程序员小田,现在在美国范德堡大学就读计算机专业。这是我的第一篇博客。作为一名在文科大校就读和来自高考大省的cs学生,其实还是蛮心累的。在以前的那种环境里,自己需要通过各种各样的方式和别
poj 3469 Dual Core CPU 最大流建图思想 dinic 弧优化很重要
http://poj.org/problem?id=3469 题意:给你n个物品,放在集合a中会有一定的花费,放在集合B中也有一定的花费,其中还有m对物体 当这m对物体放在同一个集合中不会产生额外的花费,否则会产生额外的花费,问最后最小的花费 #include <iostream>#include <cstdio>#include <cstring>#include <cstd
poj 3281 Dining 最大流dinic 模板题
http://poj.org/problem?id=3281 题意:有n头牛,每头牛喜欢吃几种对应的饮料和食物(不同牛喜欢的种类可能不同),求怎样分配 使得能同时吃到喜欢的饮料和食物的牛的个数最多; #include <iostream>#include <cstdio>#include <cstring>#include <cstdlib>#include <cmath>#incl
最大流Dinic C语言实现(详细)--poj 3281
//Dinic最大的不同就是分层找增长路径。。。,//我们知道一般是用BFS来找一个增长路径,从中心一层一层地向外扩散//但是Dinic也是一层一层的向外找,但是它每层只选择一个一个顶点就跳到下一层中接着寻找#include<stdio.h>#define N 1000#define MAX 0x3f3f3f3f#define min(x,y) ((x>y)?(y):(x))//定
最大流dinic算法分析
Dinic算法是一种比较容易实现的,相对比较快的最大流算法。 今天看了一下它的原理,发现的确很牛逼。 求最大流的本质,就是不停的寻找增广路径。直到找不到增广路径为止。 对于这个一般性的过程,Dinic算法的优化如下: (1) Dinic算法首先对图进行一次BFS,然后在BFS生成的层次图中进行多次DFS。 层次图的意思就是,只有在BFS树中深度相差1的节点才是连接的。 这就切断了原有的图中的
2172. Dinic/ISAP求最大流 (Dinic算法)
2172. Dinic/ISAP求最大流 - AcWing题库 给定一个包含 n 个点 m 条边的有向图,并给定每条边的容量,边的容量非负。 图中可能存在重边和自环。求从点 S 到点 T 的最大流。 输入格式 第一行包含四个整数 n,m,S,T。 接下来 m 行,每行三个整数 u,v,c,表示从点 u 到点 v 存在一条有向边,容量为 c。 点的编号从 1 到 n。 输出格式 输出
网络流最大流 Dinic算法
O(N^2*M)的算法 比EK的O(N*M^2)优很多 EK通常解决10^3 –10^4规模的网络 而dinic能解决10^4–10^5的网络 Dinic算法的思想也是分阶段地在层次网络中增广。它与最短增广路算法不同之处是:最短增广路每个阶段执行完一次BFS增广后,要重新启动BFS从源点Vs开始寻找另一条增广路;而在Dinic算法中,只需一次DFS过程就可以实现多次增广,这是Dinic算法
@2017-2018 ACM-ICPC, Asia Daejeon Regional Contest H; How Many to Be Happy? ( 最小割 dinic算法)
时间限制: 1 Sec 内存限制: 128 MB 提交: 80 解决: 32 [提交] [状态] [讨论版] [命题人:admin] 题目描述 Let G be a connected simple undirected graph where each edge has an associated weight. Let’s consider the popular MST (Mini
POJ 2391 Ombrophobic Bovines(二分+floyd+拆点+Dinic网络流)
题意:有n个田地,给出每个田地上初始的牛的数量和每个田地可以容纳的牛的数量。m条双向的路径,每条路径上可以同时通过的牛没有限制。 问牛要怎么走,能在最短时间内使得每块田地都能容纳的下,输出最短时间或-1。 分析:先floyd求出任意两点之间的最短距离,然后二分答案,判断是否可以在时间不超过mid的情况下完成移动: 建图: 每个点拆成两个点x(i)和x'(i+n),源点向x连边,权值
dinic当前弧优化板子
洛谷的板题https://www.luogu.org/problemnew/show/P3376 #include <cstdio>#include <cstring>#include <queue>#include <algorithm>using namespace std;const int MAX = (1ll << 31) - 1;long long read(){long lo