本文主要是介绍POJ训练计划1459_Power Network(网络流最大流/Dinic),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
解题报告
这题建模实在是好建,,,好贱,,,
给前向星给跪了,纯dinic的前向星竟然TLE,sad,,,回头看看优化,,,
矩阵跑过了,2A,sad,,,
/*************************************************************************> File Name: PowerN.cpp> Author: _nplus> Mail: jun18753370216@gmail.com> Time: 2014年07月19日 星期六 09时30分23秒************************************************************************/#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
#include<iostream>
#include<algorithm>
#define inf 99999999
#define N 510
#define M N*N
using namespace std;
int edge[N][N],l[N],n,m,nc,np;
int bfs()
{queue<int >Q;memset(l,-1,sizeof(l));while(!Q.empty())Q.pop();l[n]=0;Q.push(n);while(!Q.empty()){int u=Q.front();Q.pop();for(int i=0; i<=n+1; i++){if(edge[u][i]&&l[i]==-1){l[i]=l[u]+1;Q.push(i);}}}if(l[n+1]>0)return 1;else return 0;
}
int dfs(int x,int f)
{if(x==n+1)return f;int a;for(int i=0; i<=n+1; i++){if(edge[x][i]&&(l[i]==l[x]+1)&&(a=dfs(i,min(edge[x][i],f)))){edge[x][i]-=a;edge[i][x]+=a;return a;}}l[x]=-1;//加上时间优化了15倍,,,sad,,,return 0;
}
int main()
{int i,j,u,v,w;while(~scanf("%d%d%d%d",&n,&np,&nc,&m)){memset(edge,0,sizeof(edge));for(i=0; i<m; i++){while(getchar()!='(');scanf("%d,%d)%d",&u,&v,&w);edge[u][v]=w;}for(i=0; i<np; i++){while(getchar()!='(');scanf("%d)%d",&v,&w);edge[n][v]=w;}for(i=0; i<nc; i++){while(getchar()!='(');scanf("%d)%d",&u,&w);edge[u][n+1]=w;}int a,flow=0;while(bfs()){while(a=dfs(n,inf)){flow+=a;}}printf("%d\n",flow);}
}
写写EK算法,,,竟然比我写的Dinic快,,,看来我的模板问题不少,,,sad,,,
/*************************************************************************> File Name: PowerN.cpp> Author: _nplus> Mail: jun18753370216@gmail.com> Time: 2014年07月19日 星期六 09时30分23秒************************************************************************/#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
#include<iostream>
#include<algorithm>
#define inf 99999999
#define N 510
#define M N*N
using namespace std;
int edge[N][N],pre[N],a[N],n,m,nc,np,flow;
void ek()
{while(1){queue<int >Q;Q.push(n);memset(pre,-1,sizeof(pre));memset(a,0,sizeof(a));a[n]=inf;pre[n]=n;while(!Q.empty()){int u=Q.front();Q.pop();for(int v=0;v<=n+1;v++){if(edge[u][v]&&!a[v]){pre[v]=u;a[v]=min(a[u],edge[u][v]);Q.push(v);}}if(a[n+1])break;}if(!a[n+1])break;for(int u=n+1;u!=n;u=pre[u]){edge[pre[u]][u]-=a[n+1];edge[u][pre[u]]+=a[n+1];}flow+=a[n+1];}
}
int main()
{int i,j,u,v,w;while(~scanf("%d%d%d%d",&n,&np,&nc,&m)){memset(edge,0,sizeof(edge));for(i=0; i<m; i++){while(getchar()!='(');scanf("%d,%d)%d",&u,&v,&w);edge[u][v]=w;}for(i=0; i<np; i++){while(getchar()!='(');scanf("%d)%d",&v,&w);edge[n][v]=w;}for(i=0; i<nc; i++){while(getchar()!='(');scanf("%d)%d",&u,&w);edge[u][n+1]=w;}int a;flow=0;ek();printf("%d\n",flow);}
}
Power Network
| Time Limit: 2000MS | Memory Limit: 32768K | |
| Total Submissions: 22571 | Accepted: 11819 |
Description
A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amount s(u) >= 0 of power, may produce an amount 0 <= p(u) <= p max(u) of power, may consume an amount 0 <= c(u) <= min(s(u),c max(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= l max(u,v) of power delivered by u to v. Let Con=Σ uc(u) be the power consumed in the net. The problem is to compute the maximum value of Con.
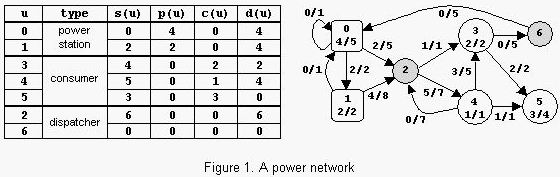
An example is in figure 1. The label x/y of power station u shows that p(u)=x and p max(u)=y. The label x/y of consumer u shows that c(u)=x and c max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6.

An example is in figure 1. The label x/y of power station u shows that p(u)=x and p max(u)=y. The label x/y of consumer u shows that c(u)=x and c max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6.
Input
There are several data sets in the input. Each data set encodes a power network. It starts with four integers: 0 <= n <= 100 (nodes), 0 <= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <= n^2 (power transport lines). Follow m data triplets (u,v)z, where u and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the value of l max(u,v). Follow np doublets (u)z, where u is the identifier of a power station and 0 <= z <= 10000 is the value of p max(u). The data set ends with nc doublets (u)z, where u is the identifier of a consumer and 0 <= z <= 10000 is the value of c max(u). All input numbers are integers. Except the (u,v)z triplets and the (u)z doublets, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.
Output
For each data set from the input, the program prints on the standard output the maximum amount of power that can be consumed in the corresponding network. Each result has an integral value and is printed from the beginning of a separate line.
Sample Input
2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20 7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7(3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5(0)5 (1)2 (3)2 (4)1 (5)4
Sample Output
15 6
Hint
The sample input contains two data sets. The first data set encodes a network with 2 nodes, power station 0 with pmax(0)=15 and consumer 1 with cmax(1)=20, and 2 power transport lines with lmax(0,1)=20 and lmax(1,0)=10. The maximum value of Con is 15. The second data set encodes the network from figure 1.
Source
这篇关于POJ训练计划1459_Power Network(网络流最大流/Dinic)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






