本文主要是介绍Stanford-Coursera 算法Week1 笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题外话:全文免费放心食用,作者在此求个 三连+关注
1. Integer Multiplication(引入)
(很小的时候我们就学过:两个数字相乘的算法——将输入(两个数字)转换为输出(它们的乘积)的一组定义良好的规则;算法就是类似的:一个计算问题(输入和期望的输出),然后描述一个或多个解决该问题的算法)
1)定义计算问题:在整数乘法问题中,输入是两个n位数,我们称之为x和y, x和y的长度n可以是任意正整数;整数乘法问题的期望输出就是x·y

2)定义primitive operations:
(i) 两个个位数相加;(ii) 两个个位数相乘;(iii)在数字的开头或结尾添加零
e.g: x = 5678 and y = 1234 (so n = 4).
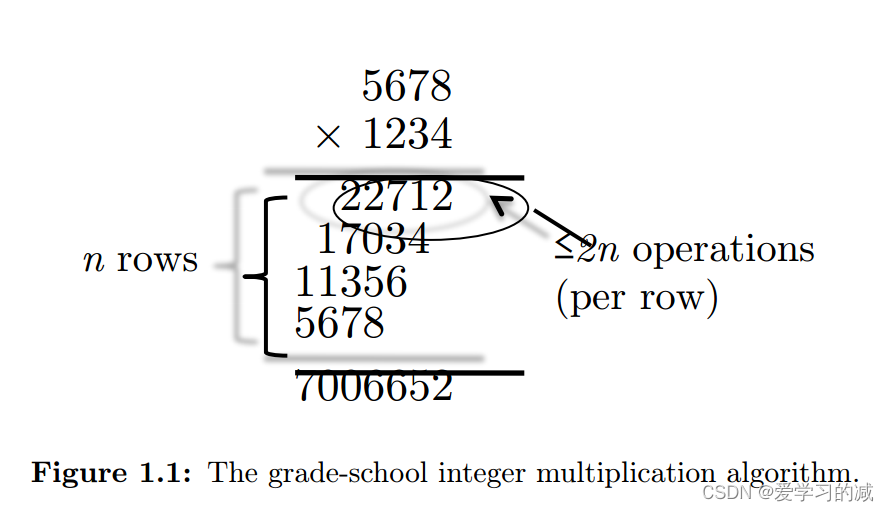
计算会有n=4行,每行最多2n个操作(primitive operations)
所以最多会有 n · 2n 次 primitive operations
3)改进——下一节 3Karatsuba Multiplication
2.Karatsuba Multiplication
1)为了将x的前半部分和后半部分看作独立的数字,a = 56,b = 78,c = 12,d = 34
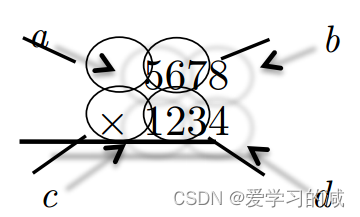
2)执行一系列只涉及两位数a, b, c和d的运算
3)将所有项集合在一起,得到x和y的乘积
第一步:计算a·c = 56·12 = 672
第二步:计算b·d = 78·34 = 2652
第三步:计算(a + b)·(c + d) = 134·46 = 6164
第四步:用第三步的结果减去前两步的结果:6164 - 672 - 2652 = 2840
第五步:计算104·672 + 102·2840 + 2652 = 6720000 + 284000 + 2652 = 70066552
2.1 A Recursive Algorithm(引入方便理解)
整数乘法递归方法
偶数n位:
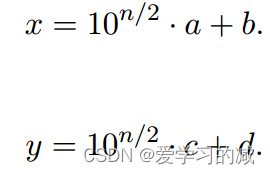
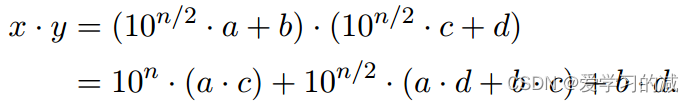
伪代码(有个印象就行):

2.2 转回Karatsuba乘法
Karatsuba乘法是RecIntMult算法的优化版本
我们并不真正关心a·d或b·c,而是它们的和a·d + b·c
因此:只有三个量——a·c, a·d + b·c和b·d
Step 1: Recursively递归 compute a · c
Step 2: Recursively compute b · d
Step 3: Compute a + b and c + d , and recursively compute (a + b) · (c + d)——至此:三次递归
Step 4:用Step 3的结果减去前两步的结果,得到a·d + b·c
Step 5:乘10n次方在step 1的answer,乘10(n/2)次方在step 3的answer,最后把所有结果相加

因此,Karatsuba乘法只进行三次递归调用! 节省递归调用可以节省总体运行时间
3.MergeSort Algorithm
特点
- Canonical divide-and-conquer algorithm 规范的分治算法:将问题分解为更小的子问题,递归地求解子问题,最后将子问题的解合并为原始问题的解
3.1 Sorting—拓展:十种基本的排序
1.0 十大经典排序算法 | 菜鸟教程 (runoob.com)
3.2 MergeSort—Example

1.递归
As a recursive divide-and-conquer algorithm作为递归分治算法, MergeSort 拆分成了两部分进行递归;第一组递归对前半部分进行排序,返回数组{1,4,5,8};第二组递归调用返回数组{2,3,6,7};最后合并两组

2.合并 Merge Subroutine 子程序

使用索引 k 遍历输出数组,并使用索引 i 和 j 遍历已排序的子数组。所有三个数组都是从左到右遍历的
第3行中的for循环实现了对输出数组的传递。在第一次迭代中,子例程识别C或D中的最小元素,并将其复制到输出数组b的第一个位置。总的来说,最小元素要么在C中(在这种情况下,它是C[1],因为C是排序的),要么在D中(在这种情况下,它是D[1],因为D是排序的)。
3.3 MergeSort—分析
因为mergesort相当于是递归+merge,所以会涉及到对递归树的分析
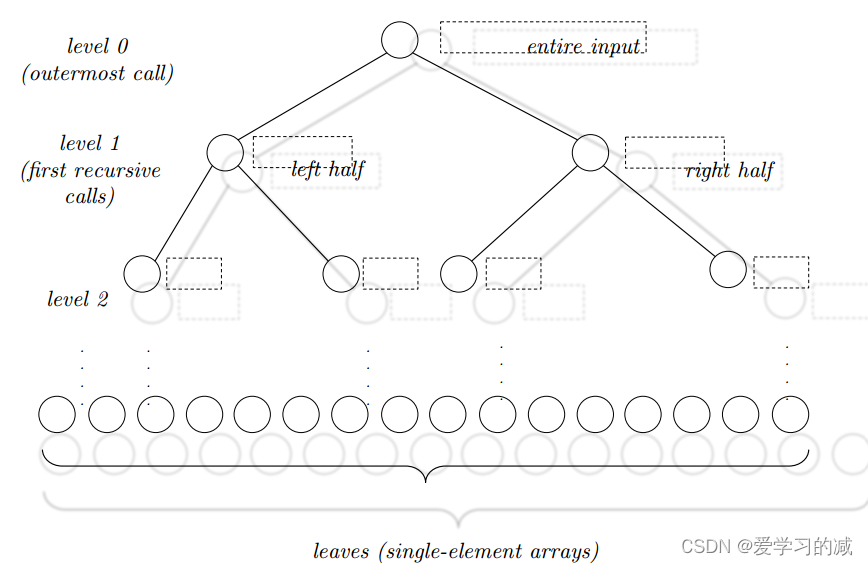
层数计算:

每一层的子问题&子问题大小:

4. Asymptotic Analysis 渐进分析
4.1 Big-O Notation 基础
是什么?
- 为了讨论算法的设计和分析——为讨论算法的high-level performance提供了一个最佳点
- 粗糙:压制住想要忽略的细节,细节取决于architecture、programming language、compiler...
- 敏锐:常见问题的不同高级算法间进行预测性比较,尤其是large inputs
“O”---为了找到解决问题的最佳高级算法
意思就是:
suppress constant factors & lower-order terms
抑制常数项和低阶项
结合下面例子:
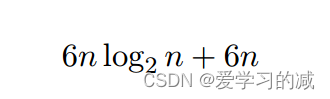
抑制6n和“6”
所以running time是“big-O of nlog n” 即 O(nlogn)
例子1:

running time:O(n)
例子2:

running time:O(n)
为啥呢?其实是2n但2被抑制了
例子3:

running time:O()
例子4:

running time:O()
解释:外部循环从1到n,内部循环从i+1到n。内部循环的迭代次数取决于外部循环的当前迭代次数。
考虑最坏的情况,数组A中的所有元素都是相同的。在这种情况下,内部循环的迭代次数为: 1 + 2 + 3 + ... + (n-1) = n*(n-1)/2,总的迭代次数为n*(n-1)/2
4.2 Big-O Notation 正式定义
Big-O notation 关注 T(n),n = 1, 2,....

这篇关于Stanford-Coursera 算法Week1 笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






