FCM聚类算法详解(Python实现iris数据集)

本文主要是介绍FCM聚类算法详解(Python实现iris数据集)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参考：https://blog.csdn.net/on2way/article/details/47087201

模糊C均值（Fuzzy C-means）算法简称FCM算法，是一种基于目标函数的模糊聚类算法，主要用于数据的聚类分析。理论成熟，应用广泛，是一种优秀的聚类算法。本文关于FCM算法的一些原理推导部分介绍，加上自己的理解和在课题项目中的应用以文字的形式呈现出来。

首先介绍一下模糊这个概念，所谓模糊就是不确定，确定性的东西就是信息量很小的东西，而不确定性的东西就说很像什么，这种信息量很大。比如说把20岁作为年轻不年轻的标准，那么一个人21岁按照确定性的划分就属于不年轻，而我们印象中的观念是21岁也很年轻，这个时候可以模糊一下，认为21岁有0.9分像年轻，有0.1分像不年轻，这里0.9与0.1不是概率，而是一种相似的程度，把这种一个样本属于结果的这种相似的程度称为样本的隶属度，一般用u表示，表示一个样本相似于不同结果的一个程度指标。

基于此，假定数据集为X，如果把这些数据划分成c类的话，那么对应的就有c个类中心为C，每个样本j属于某一类i的隶属度为uij，那么定义一个FCM目标函数（1）及其约束条件（2）如下所示：
$J=∑_{i=1}^{n}∑_{j=1}^{n}u_{ij}^{m}||xj−ci||^2 ...............................(1)$

$_{i=1}^{c}u_{ij}=1,j=1,2...,n..............................(2)$

看一下目标函数（式1）而知，由相应样本的隶属度与该样本到各个类中心的距离相乘组成的，m是一个隶属度的因子，个人理解为属于样本的轻缓程度，就像 $x^2$ 与 $x^3$ 这种一样。式（2）为约束条件，也就是一个样本属于所有类的隶属度之和要为1。观察式（1）可以发现，其中的变量有 $u_{ij}、c_i$ ，并且还有约束条件，那么如何求这个目标函数的极值呢？

这里首先采用拉格朗日乘数法将约束条件拿到目标函数中去，前面加上系数，并把式（2）的所有j展开，那么式（1）变成下列所示：

$J=∑_{i=1}^{c}∑_{j=1}^{n}u_{ij}^{m}||x_j−c_i||^2+λ_1(∑_{i=1}^{c}u_{i1}−1)+...+λ_j(∑_{i=1}^{c}u_{ij}−1)+...+λ_n(∑_{i=n}cu_{in}−1)).....................................(3)$

现在要求该式的目标函数极值，那么分别对其中的变量uij、ci求导数，首先对uij求导。

分析式(3)，先对第一部分的两级求和的uij求导，对求和形式下如果直接求导不熟悉，可以把求和展开如下：

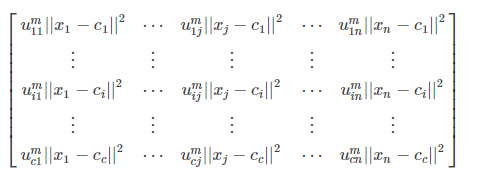
在这里插入图片描述
这个矩阵要对uij求导，可以看到只有uij对应的 $u_{m}^{ij}||x_j−c_i||^2$ 保留，其他的所有项中因为不含有uijuij，所以求导都为0。那么 $u_{ij}^{m}||x_j−c_i||^2$ 对uij求导后就为 $m||x_j−c_i||^2u_{ij}^{m-1}$ 。

再来看后面那个对uij求导，同样把求和展开，再去除和uij不相关的（求导为0），那么只剩下这一项： $λ_j(u_{ij}−1)$ ，它对uij求导就是λj了。

那么最终J对uij的求导结果并让其等于0就是：
$\frac{∂J}{∂uij}=m||x_j−c_i||^2u_{ij}^{m-1}+λ_j=0$

这个式子化简下，将uij解出来就是：

$u_{ij}^{m-1}=\frac{−λ_j}{m||xj−ci||^2}$

进一步：

$u_{ij}=(\frac{−λ_j}{m||xj−ci||^2})^\frac{1}{m−1}=(\frac{−λ_j}{m})^\frac{1}{m−1}\frac{1}{(\frac{1}{||xj−ci||})^\frac{2}{m−1}}.......(4)$

要解出uij则需要把λj去掉才行。这里重新使用公式（2）的约束条件，并把算出来的uij代入式（2）中有：
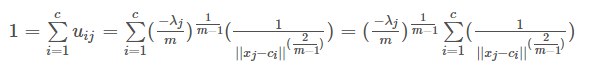
在这里插入图片描述

这样就有（其中把符号i换成k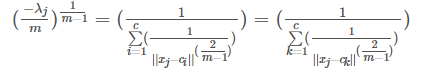）：在这里插入图片描述
把这个重新代入到式（4）中有：

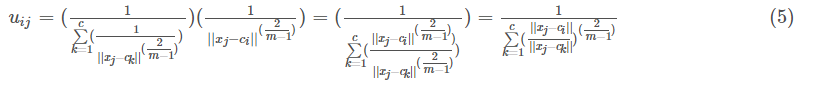
好了，式子（5）就是最终的uij迭代公式。

下面在来求J对ci的导数。由公式（2）可以看到只有 $_{i=1}^{c}∑_{j=1}^{n}u_{ij}^{m}||xj−ci||^2$ 这一部分里面含有ci，对其二级求和展开如前面所示的，那么它对ci的导数就是：
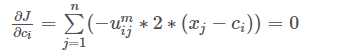
在这里插入图片描述
即：

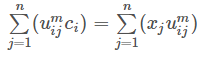
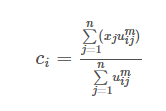
好了，公式（6）就是类中心的迭代公式。

我们发现uij与ci是相互关联的，彼此包含对方，有一个问题就是在fcm算法开始的时候既没有uij也没有ci，那要怎么求解呢？很简单，程序开始的时候我们随便赋值给uij或者ci其中的一个，只要数值满足条件即可。然后就开始迭代，比如一般的都赋值给uij，那么有了uij就可以计算ci，然后有了ci又可以计算uij，反反复复，在这个过程中还有一个目标函数J一直在变化，逐渐趋向稳定值。那么当J不在变化的时候就认为算法收敛到一个比较好的解了。可以看到uij和ci在目标函数J下似乎构成了一个正反馈一样，这一点很像EM算法，先E在M，有了M在E，在M直至达到最优。

公式（5），（6）是算法的关键。现在来重新从宏观的角度来整体看看这两个公式，先看（5），在写一遍

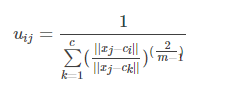
在这里插入图片描述
假设看样本集中的样本1到各个类中心的隶属度，那么此时j=1，i从1到c类，此时上述式中分母里面求和中，分子就是这个点相对于某一类的类中心距离，而分母是这个点相对于所有类的类中心的距离求和，那么它们两相除表示什么，是不是表示这个点到某个类中心在这个点到所有类中心的距离和的比重。当求和里面的分子越小，是不是说就越接近于这个类，那么整体这个分数就越大，也就是对应的uij就越大，表示越属于这个类，形象的图如下：
在这里插入图片描述
再来宏观看看公式（6），考虑当类i确定后，式（6）的分母求和其实是一个常数，那么式（6）可以写成：

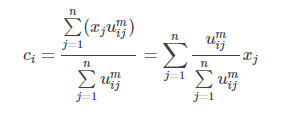
这是类中心的更新法则。说这之前，首先让我们想想kmeans的类中心是怎么更新的，一般最简单的就是找到属于某一类的所有样本点，然后这一类的类中心就是这些样本点的平均值。那么FCM类中心怎么样了？看式子可以发现也是一个加权平均，类i确定后，首先将所有点到该类的隶属度u求和，然后对每个点，隶属度除以这个和就是所占的比重，乘以xj就是这个点对于这个类i的贡献值了。画个形象的图如下：
在这里插入图片描述
由上述的宏观分析可知，这两个公式的迭代关系式是这样的也是可以理解的。

数据集用的是iris数据，有需要数据的朋友可以调用sklearn.load_iris。或者下载下来

from pylab import *
from numpy import *
import pandas as pd
import numpy as np
import operator
import math
import matplotlib.pyplot as plt
import random# 数据保存在.csv文件中
df_full = pd.read_csv("iris.csv")
columns = list(df_full.columns)
features = columns[:len(columns) - 1]
# class_labels = list(df_full[columns[-1]])
df = df_full[features]
# 维度
num_attr = len(df.columns) - 1
# 分类数
k = 3
# 最大迭代数
MAX_ITER = 100
# 样本数
n = len(df)  # the number of row
# 模糊参数
m = 2.00# 初始化模糊矩阵U
def initializeMembershipMatrix():membership_mat = list()for i in range(n):random_num_list = [random.random() for i in range(k)]summation = sum(random_num_list)temp_list = [x / summation for x in random_num_list]  # 首先归一化membership_mat.append(temp_list)return membership_mat# 计算类中心点
def calculateClusterCenter(membership_mat):cluster_mem_val = zip(*membership_mat)cluster_centers = list()cluster_mem_val_list = list(cluster_mem_val)for j in range(k):x = cluster_mem_val_list[j]xraised = [e ** m for e in x]denominator = sum(xraised)temp_num = list()for i in range(n):data_point = list(df.iloc[i])prod = [xraised[i] * val for val in data_point]temp_num.append(prod)numerator = map(sum, zip(*temp_num))center = [z / denominator for z in numerator]  # 每一维都要计算。cluster_centers.append(center)return cluster_centers# 更新隶属度
def updateMembershipValue(membership_mat, cluster_centers):#    p = float(2/(m-1))data = []for i in range(n):x = list(df.iloc[i])  # 取出文件中的每一行数据data.append(x)distances = [np.linalg.norm(list(map(operator.sub, x, cluster_centers[j]))) for j in range(k)]for j in range(k):den = sum([math.pow(float(distances[j] / distances[c]), 2) for c in range(k)])membership_mat[i][j] = float(1 / den)return membership_mat, data# 得到聚类结果
def getClusters(membership_mat):cluster_labels = list()for i in range(n):max_val, idx = max((val, idx) for (idx, val) in enumerate(membership_mat[i]))cluster_labels.append(idx)return cluster_labelsdef fuzzyCMeansClustering():# 主程序membership_mat = initializeMembershipMatrix()curr = 0while curr <= MAX_ITER:  # 最大迭代次数cluster_centers = calculateClusterCenter(membership_mat)membership_mat, data = updateMembershipValue(membership_mat, cluster_centers)cluster_labels = getClusters(membership_mat)curr += 1print(membership_mat)return cluster_labels, cluster_centers, data, membership_matdef xie_beni(membership_mat, center, data):sum_cluster_distance = 0min_cluster_center_distance = inffor i in range(k):for j in range(n):sum_cluster_distance = sum_cluster_distance + membership_mat[j][i] ** 2 * sum(power(data[j, :] - center[i, :], 2))  # 计算类一致性for i in range(k - 1):for j in range(i + 1, k):cluster_center_distance = sum(power(center[i, :] - center[j, :], 2))  # 计算类间距离if cluster_center_distance < min_cluster_center_distance:min_cluster_center_distance = cluster_center_distancereturn sum_cluster_distance / (n * min_cluster_center_distance)labels, centers, data, membership = fuzzyCMeansClustering()
print(labels)
print(centers)
center_array = array(centers)
label = array(labels)
datas = array(data)# Xie-Beni聚类有效性
print("聚类有效性：", xie_beni(membership, center_array, datas))
xlim(0, 10)
ylim(0, 10)
# 做散点图
fig = plt.gcf()
fig.set_size_inches(16.5, 12.5)
f1 = plt.figure(1)
plt.scatter(datas[nonzero(label == 0), 0], datas[nonzero(label == 0), 1], marker='o', color='r', label='0', s=10)
plt.scatter(datas[nonzero(label == 1), 0], datas[nonzero(label == 1), 1], marker='+', color='b', label='1', s=10)
plt.scatter(datas[nonzero(label == 2), 0], datas[nonzero(label == 2), 1], marker='*', color='g', label='2', s=10)
plt.scatter(center_array[:, 0], center_array[:, 1], marker='x', color='m', s=30)
plt.show()