本文主要是介绍基于卷积神经网络CNN,使用二维卷积Conv2D实现MNIST数字识别的四种方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

前言
系列专栏:机器学习:高级应用与实践【项目实战100+】【2024】✨︎
在本专栏中不仅包含一些适合初学者的最新机器学习项目,每个项目都处理一组不同的问题,包括监督和无监督学习、分类、回归和聚类,而且涉及创建深度学习模型、处理非结构化数据以及指导复杂的模型,如卷积神经网络、门控循环单元、大型语言模型和强化学习模型
使用 MNIST 数据集进行手写数字识别是一个借助神经网络完成的重要项目。深度神经网络是机器学习和人工智能的一个分支,这种网络能够从提供的无组织或无标记数据中进行无监督学习。
我们在此基础上更进一步,我们的手写数字识别系统不仅能检测手写数字的扫描图像,还能借助集成的图形用户界面在屏幕上书写数字进行识别。它主要检测手写数字的扫描图像。
目录
- 1. 相关库和数据集
- 1.1 相关库介绍
- 1.2 数据集介绍
- 2. 数据预处理
- 2.1 特征缩放
- 2.2 数据重塑
- 2.3 格式变换
- 3. 模型建立
- 3.1 数据准备
- 3.2 构建模型(4 种不同的模型结构)
- 3.2.1 密集神经网络
- 3.2.2 二维卷积网络(密集+最大池化)
- 3.2.3 二维卷积网络(密集+最大池化+Dropout)
- 3.2.4 二维卷积网络(密集+最大池化+Dropout+BN算法)
- 4. 模型评估
- 4.1 预测性能
- 4.2 比較結果
- 4.3 结果可视化
1. 相关库和数据集
1.1 相关库介绍
Python 库使我们能够非常轻松地处理数据并使用一行代码执行典型和复杂的任务。
Numpy– 是一种开源的数值计算扩展,可用来存储和处理大型矩阵,缩短大型计算的时间。Matplotlib– 此库用于绘制可视化效果,用于展现数据之间的相互关系。TensorFlow™– 是一个基于数据流编程的符号数学系统,被广泛应用于各类机器学习算法的编程实现。Keras– 是一个由Python编写的开源人工神经网络库,可以作为Tensorflow的高阶应用程序接口,进行深度学习模型的设计、调试、评估、应用和可视化。
import numpy as np
import matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_split
import tensorflow as tffrom tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.datasets import mnist
from keras.utils import to_categorical
1.2 数据集介绍
MNIST 数据集是一组由中学生和美国人口普查局雇员手写的 70,000 个小图,由高中生和美国人口普查局的员工手写而成。每个图像都标有所代表的数字,人们对该数据集进行了大量研究,因此它经常被称为机器学习的 “Hello World”。
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print("Training Shape:", x_train.shape, y_train.shape)
print("----------------------------------------")
print("Testing Shape:", x_test.shape, y_test.shape)
Training Shape: (60000, 28, 28) (60000,)
----------------------------------------
Testing Shape: (10000, 28, 28) (10000,)
2. 数据预处理
2.1 特征缩放
①将像素值(0-255)归一化为(0-1),以便更好地进行训练
# Normalize pixel values (0-255) to (0-1) --> 0 for better training
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0print("Min: %.3f, Max: %.3f" % (x_train.min(), x_train.max()))
print("Min: %.3f, Max: %.3f" % (x_test.min(), x_test.max()))
Min: 0.000, Max: 1.000
Min: 0.000, Max: 1.000
2.2 数据重塑
②重塑数据以便输入神经网络
# Reshape the data for input to the neural network (28x28 pixels)
x_train = x_train.reshape((x_train.shape[0], 28, 28, 1))
x_test = x_test.reshape((x_test.shape[0], 28, 28, 1))print("Training Shape:", x_train.shape)
print("----------------------------")
print("Testing Shape:", x_test.shape)
Training Shape: (60000, 28, 28, 1)
----------------------------
Testing Shape: (10000, 28, 28, 1)
2.3 格式变换
③将标签从整数格式转换为 one-hot 编码向量
y_train = to_categorical(y_train, num_classes=10)
y_test = to_categorical(y_test, num_classes=10)print(y_train[0])
print(y_test[0])
[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
3. 模型建立
3.1 数据准备
①将数据拆分为训练数据、验证数据和测试数据
x_train, x_val, y_train, y_val = train_test_split(x_train, y_train, test_size=0.20, random_state=1)
print("Training Shape:", x_train.shape, y_train.shape)
print("------------------------------------------")
print("validation Shape:", x_val.shape, y_val.shape)
Training Shape: (48000, 28, 28, 1) (48000, 10)
------------------------------------------
validation Shape: (12000, 28, 28, 1) (12000, 10)
3.2 构建模型(4 种不同的模型结构)
3.2.1 密集神经网络
# 使用Sequential模型,并通过Input层指定输入形状
model_1 = keras.Sequential([layers.Input(shape=(28, 28, 1)), # 这里的Input层定义了模型的输入形状layers.Flatten(),layers.Dense(512, activation='relu'),layers.Dense(256, activation='relu'),layers.Dense(10, activation='softmax')
])
# compile the model
model_1.compile(optimizer= 'adam',loss='categorical_crossentropy',metrics=['accuracy']
)
模型概要
model_1.summary()
Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ flatten (Flatten) │ (None, 784) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense (Dense) │ (None, 512) │ 401,920 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_1 (Dense) │ (None, 256) │ 131,328 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_2 (Dense) │ (None, 10) │ 2,570 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘Total params: 535,818 (2.04 MB)Trainable params: 535,818 (2.04 MB)Non-trainable params: 0 (0.00 B)
模型训练
model_1.fit(x_train, y_train, validation_data=(x_val, y_val), epochs=10, batch_size=32)
Epoch 1/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 6s 4ms/step - accuracy: 0.8948 - loss: 0.3426 - val_accuracy: 0.9642 - val_loss: 0.1150
Epoch 2/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.9745 - loss: 0.0825 - val_accuracy: 0.9719 - val_loss: 0.0933
Epoch 3/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 5s 3ms/step - accuracy: 0.9829 - loss: 0.0534 - val_accuracy: 0.9727 - val_loss: 0.0980
Epoch 4/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.9865 - loss: 0.0380 - val_accuracy: 0.9709 - val_loss: 0.1073
Epoch 5/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.9892 - loss: 0.0302 - val_accuracy: 0.9778 - val_loss: 0.0905
Epoch 6/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.9927 - loss: 0.0225 - val_accuracy: 0.9760 - val_loss: 0.1015
Epoch 7/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.9936 - loss: 0.0186 - val_accuracy: 0.9775 - val_loss: 0.0990
Epoch 8/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 5s 3ms/step - accuracy: 0.9933 - loss: 0.0196 - val_accuracy: 0.9778 - val_loss: 0.1068
Epoch 9/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.9939 - loss: 0.0182 - val_accuracy: 0.9772 - val_loss: 0.1158
Epoch 10/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.9938 - loss: 0.0182 - val_accuracy: 0.9770 - val_loss: 0.1083
模型评估
test_loss_1, test_accuracy_1 = model_1.evaluate(x_test, y_test)print("\nAccuracy =", test_accuracy_1, "\n-----------------------------", "\nLoss =", test_loss_1)
313/313 ━━━━━━━━━━━━━━━━━━━━ 2s 5ms/step - accuracy: 0.9749 - loss: 0.1182Accuracy = 0.978600025177002
-----------------------------
Loss = 0.09816069155931473
3.2.2 二维卷积网络(密集+最大池化)
model_2 = keras.Sequential([layers.Input(shape=(28, 28, 1)),layers.Conv2D(32, (3,3), activation='relu'),layers.MaxPooling2D((2,2)),layers.Conv2D(64, (3,3), activation='relu'),layers.MaxPooling2D((2,2)),layers.Flatten(),layers.Dense(128, activation='relu'),layers.Dense(10, activation='softmax')
])
# compile the model
model_2.compile(optimizer= 'Adam',loss='categorical_crossentropy',metrics=['accuracy']
)
模型概要
model_2.summary()
Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ conv2d (Conv2D) │ (None, 26, 26, 32) │ 320 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d (MaxPooling2D) │ (None, 13, 13, 32) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_1 (Conv2D) │ (None, 11, 11, 64) │ 18,496 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_1 (MaxPooling2D) │ (None, 5, 5, 64) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten_1 (Flatten) │ (None, 1600) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_3 (Dense) │ (None, 128) │ 204,928 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_4 (Dense) │ (None, 10) │ 1,290 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘Total params: 225,034 (879.04 KB)Trainable params: 225,034 (879.04 KB)Non-trainable params: 0 (0.00 B)
模型训练
model_2.fit(x_train, y_train, batch_size=32, validation_data=(x_val, y_val), epochs=10)
Epoch 1/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9023 - loss: 0.3260 - val_accuracy: 0.9793 - val_loss: 0.0674
Epoch 2/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9849 - loss: 0.0485 - val_accuracy: 0.9789 - val_loss: 0.0650
Epoch 3/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9909 - loss: 0.0299 - val_accuracy: 0.9829 - val_loss: 0.0585
Epoch 4/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9933 - loss: 0.0195 - val_accuracy: 0.9861 - val_loss: 0.0483
Epoch 5/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9937 - loss: 0.0173 - val_accuracy: 0.9868 - val_loss: 0.0493
Epoch 6/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9964 - loss: 0.0112 - val_accuracy: 0.9873 - val_loss: 0.0515
Epoch 7/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9963 - loss: 0.0101 - val_accuracy: 0.9865 - val_loss: 0.0533
Epoch 8/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9963 - loss: 0.0098 - val_accuracy: 0.9867 - val_loss: 0.0603
Epoch 9/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9979 - loss: 0.0058 - val_accuracy: 0.9880 - val_loss: 0.0528
Epoch 10/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.9983 - loss: 0.0052 - val_accuracy: 0.9884 - val_loss: 0.0608
模型评估
test_loss_2, test_accuracy_2 = model_2.evaluate(x_test, y_test)print("\nAccuracy =", test_accuracy_2, "\n-----------------------------", "\nLoss =", test_loss_2)
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9851 - loss: 0.0610Accuracy = 0.9889000058174133
-----------------------------
Loss = 0.046354446560144424
3.2.3 二维卷积网络(密集+最大池化+Dropout)
model_3 = keras.Sequential([layers.Input(shape=(28, 28, 1)),layers.Conv2D(32, (3,3), activation='relu'),layers.MaxPooling2D((2,2)),layers.Conv2D(64, (3,3), activation='relu'),layers.MaxPooling2D((2,2)),layers.Conv2D(128, (3,3), activation='relu'),layers.Flatten(),layers.Dropout(0.5),layers.Dense(128, activation='relu'),layers.Dropout(0.5),layers.Dense(10, activation='softmax')
])
model_3.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy']
)
模型概要
model_3.summary()
Model: "sequential_2"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ conv2d_2 (Conv2D) │ (None, 26, 26, 32) │ 320 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_2 (MaxPooling2D) │ (None, 13, 13, 32) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_3 (Conv2D) │ (None, 11, 11, 64) │ 18,496 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_3 (MaxPooling2D) │ (None, 5, 5, 64) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_4 (Conv2D) │ (None, 3, 3, 128) │ 73,856 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten_2 (Flatten) │ (None, 1152) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout (Dropout) │ (None, 1152) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_5 (Dense) │ (None, 128) │ 147,584 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_1 (Dropout) │ (None, 128) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_6 (Dense) │ (None, 10) │ 1,290 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘Total params: 241,546 (943.54 KB)Trainable params: 241,546 (943.54 KB)Non-trainable params: 0 (0.00 B)
模型训练
model_3.fit(x_train, y_train, batch_size=32, validation_data=(x_val, y_val), epochs=10)
Epoch 1/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 9s 5ms/step - accuracy: 0.8248 - loss: 0.5350 - val_accuracy: 0.9796 - val_loss: 0.0631
Epoch 2/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9706 - loss: 0.0949 - val_accuracy: 0.9853 - val_loss: 0.0475
Epoch 3/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9805 - loss: 0.0652 - val_accuracy: 0.9874 - val_loss: 0.0422
Epoch 4/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9840 - loss: 0.0566 - val_accuracy: 0.9894 - val_loss: 0.0381
Epoch 5/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 10s 5ms/step - accuracy: 0.9867 - loss: 0.0456 - val_accuracy: 0.9895 - val_loss: 0.0380
Epoch 6/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9879 - loss: 0.0389 - val_accuracy: 0.9900 - val_loss: 0.0338
Epoch 7/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9888 - loss: 0.0378 - val_accuracy: 0.9896 - val_loss: 0.0367
Epoch 8/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9906 - loss: 0.0332 - val_accuracy: 0.9872 - val_loss: 0.0484
Epoch 9/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9901 - loss: 0.0338 - val_accuracy: 0.9917 - val_loss: 0.0319
Epoch 10/10
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 8s 5ms/step - accuracy: 0.9913 - loss: 0.0263 - val_accuracy: 0.9911 - val_loss: 0.0346
模型评估
test_loss_3, test_accuracy_3 = model_3.evaluate(x_test, y_test)print("\nAccuracy =", test_accuracy_3, "\n-----------------------------", "\nLoss =", test_loss_3)
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9883 - loss: 0.0389Accuracy = 0.991100013256073
-----------------------------
Loss = 0.030680162832140923
3.2.4 二维卷积网络(密集+最大池化+Dropout+BN算法)
model_4 = keras.Sequential([layers.Input(shape=(28, 28, 1)),layers.Conv2D(32, (3,3), activation='relu'),layers.BatchNormalization(),layers.MaxPooling2D((2,2)),layers.Conv2D(64, (3,3), activation='relu'),layers.BatchNormalization(),layers.MaxPooling2D((2,2)),layers.Conv2D(128, (3,3), activation='relu'),layers.Flatten(),layers.Dropout(0.2), # using 20% dropout instead of 50%layers.Dense(128, activation='relu'),layers.Dropout(0.2),layers.Dense(10, activation='softmax'),
])
model_4.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy']
)
模型概要
model_4.summary()
Model: "sequential_3"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ conv2d_5 (Conv2D) │ (None, 26, 26, 32) │ 320 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization │ (None, 26, 26, 32) │ 128 │
│ (BatchNormalization) │ │ │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_4 (MaxPooling2D) │ (None, 13, 13, 32) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_6 (Conv2D) │ (None, 11, 11, 64) │ 18,496 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ batch_normalization_1 │ (None, 11, 11, 64) │ 256 │
│ (BatchNormalization) │ │ │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_5 (MaxPooling2D) │ (None, 5, 5, 64) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_7 (Conv2D) │ (None, 3, 3, 128) │ 73,856 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten_3 (Flatten) │ (None, 1152) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_2 (Dropout) │ (None, 1152) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_7 (Dense) │ (None, 128) │ 147,584 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout_3 (Dropout) │ (None, 128) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_8 (Dense) │ (None, 10) │ 1,290 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘Total params: 241,930 (945.04 KB)Trainable params: 241,738 (944.29 KB)Non-trainable params: 192 (768.00 B)
模型训练
model_4.fit(x_train, y_train, batch_size=64, validation_data=(x_val, y_val), epochs=6)
Epoch 1/6
750/750 ━━━━━━━━━━━━━━━━━━━━ 12s 14ms/step - accuracy: 0.9043 - loss: 0.3018 - val_accuracy: 0.9855 - val_loss: 0.0485
Epoch 2/6
750/750 ━━━━━━━━━━━━━━━━━━━━ 10s 13ms/step - accuracy: 0.9841 - loss: 0.0517 - val_accuracy: 0.9862 - val_loss: 0.0458
Epoch 3/6
750/750 ━━━━━━━━━━━━━━━━━━━━ 10s 13ms/step - accuracy: 0.9882 - loss: 0.0379 - val_accuracy: 0.9881 - val_loss: 0.0442
Epoch 4/6
750/750 ━━━━━━━━━━━━━━━━━━━━ 10s 13ms/step - accuracy: 0.9906 - loss: 0.0286 - val_accuracy: 0.9873 - val_loss: 0.0452
Epoch 5/6
750/750 ━━━━━━━━━━━━━━━━━━━━ 10s 13ms/step - accuracy: 0.9923 - loss: 0.0252 - val_accuracy: 0.9845 - val_loss: 0.0545
Epoch 6/6
750/750 ━━━━━━━━━━━━━━━━━━━━ 10s 13ms/step - accuracy: 0.9923 - loss: 0.0236 - val_accuracy: 0.9871 - val_loss: 0.0486
模型评估
test_loss_4, test_accuracy_4 = model_4.evaluate(x_test, y_test)print("\nAccuracy =", test_accuracy_4, "\n-----------------------------", "\nLoss =", test_loss_4)
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9856 - loss: 0.0679Accuracy = 0.9901000261306763
-----------------------------
Loss = 0.04728936031460762
4. 模型评估
4.1 预测性能
①构建模型性能预测函数
def predict(model, image):reshaped_image = image.reshape((1, 28, 28, 1))prediction = model.predict(reshaped_image)predicted_class = np.argmax(prediction)return predicted_class
predict_image_class = predict(model_1, x_test[0])
print("Predicted Class Label: ", predict_image_class)
print("Actual Class Label of the same image:",(np.argmax(y_test[0])))
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
Predicted Class Label: 7
Actual Class Label of the same image: 7
4.2 比較結果
def compare_models(models, x_test, y_test):accuracies = []model_names = []for model in models:_, accuracy = model.evaluate(x_test, y_test)accuracies.append(accuracy)best_model_index = np.argmax(accuracies)best_model = models[best_model_index]best_accuracy = accuracies[best_model_index]model_names = [f"Model {i+1}" for i in range(len(models))]plt.plot(model_names, accuracies, marker='o')plt.xlabel('Models')plt.ylabel('Accuracy')plt.title('Comparison of Model Accuracies')plt.xticks(rotation=45)plt.show()print("Comparison Results:")for i in range(len(models)):print(f"Model {i+1} - Accuracy: { accuracies[i]:.4f}")print(f"Best Model : Model {best_model_index+1}")print(f"Best Accuracy: {best_accuracy:.4f}")return best_model
models = [model_1, model_2, model_3, model_4]
best_model = compare_models(models, x_test, y_test)
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9749 - loss: 0.1182
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9851 - loss: 0.0610
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9883 - loss: 0.0389
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - accuracy: 0.9856 - loss: 0.0679
4.3 结果可视化
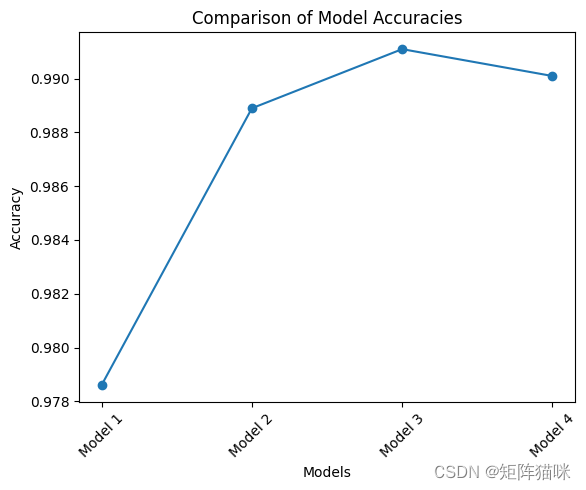
Comparison Results:
Model 1 - Accuracy: 0.9786
Model 2 - Accuracy: 0.9889
Model 3 - Accuracy: 0.9911
Model 4 - Accuracy: 0.9901
Best Model : Model 3
Best Accuracy: 0.9911
这篇关于基于卷积神经网络CNN,使用二维卷积Conv2D实现MNIST数字识别的四种方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



