本文主要是介绍【智能优化算法】蛛蜂优化算法(Spider Wasp Optimizer,SWO),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
蛛蜂优化算法(Spider Wasp Optimizer,SWO)是期刊“ARTIFICIAL INTELLIGENCE REVIEW”(中科院二区 IF=11.6)的2023年智能优化算法
01.引言
蛛蜂优化算法(Spider Wasp Optimizer,SWO)基于对自然界中雌性黄蜂的狩猎、筑巢和交配行为的复制。该算法具有多种独特的更新策略,适用于各种具有不同勘探开发要求的优化问题。
02.优化算法的流程

本文介绍了一种新的优化算法,该算法的灵感来自于某些种类的黄蜂的狩猎和筑巢行为,以及它们的专性幼虫寄生,即在每只蜘蛛的腹部产一个卵。首先,雌性蜘蛛黄蜂在周围环境中寻找合适的蜘蛛,将它们麻痹并拖到预先准备好的合适的巢穴中;这种行为代表了我们提出的算法的第一个灵感:SWO。在找到合适的猎物和巢穴并把它们拖进这些巢穴后,它们会在树上产卵蜘蛛腹部,合上巢。该算法在搜索空间内随机分布一定数量的雌蜂。然后,每只蜘蛛将在不断运动的搜索空间中寻找适合其后代性别的蜘蛛,这是由所有膜翅目昆虫中发现的单倍体性别决定系统根据它们的狩猎行为(即狩猎和跟随行为)决定的。在找到合适的蜘蛛后,雌性蜘蛛黄蜂会在它们的网中心搜寻它们,并在地上搜寻六次,寻找从网上掉下来的蜘蛛(Rayor 1996)。之后,雌黄蜂会攻击猎物,并试图麻痹它,把它拖到预先准备好的巢穴。
然后,她在蜘蛛的腹部下一个蛋后关闭巢穴。简而言之,本工作模拟的黄蜂行为如下:•搜索行为:该行为在优化开始时寻找猎物,寻找适合幼虫生长的蜘蛛。
•跟随和逃跑行为:在发现猎物/蜘蛛后,它们可能会试图逃离中心的球体。因此,雌黄蜂跟着它们,麻痹并拖拽最合适的一个。
•筑巢行为:这将模拟将猎物拖到适合猎物和蛋大小的巢穴的方式。
•交配行为:这种行为模拟了通过在雄性和雌性黄蜂之间使用统一的交叉操作来孵化卵所产生的后代的特性,该操作具有特定的概率,称为交叉率(CR)。

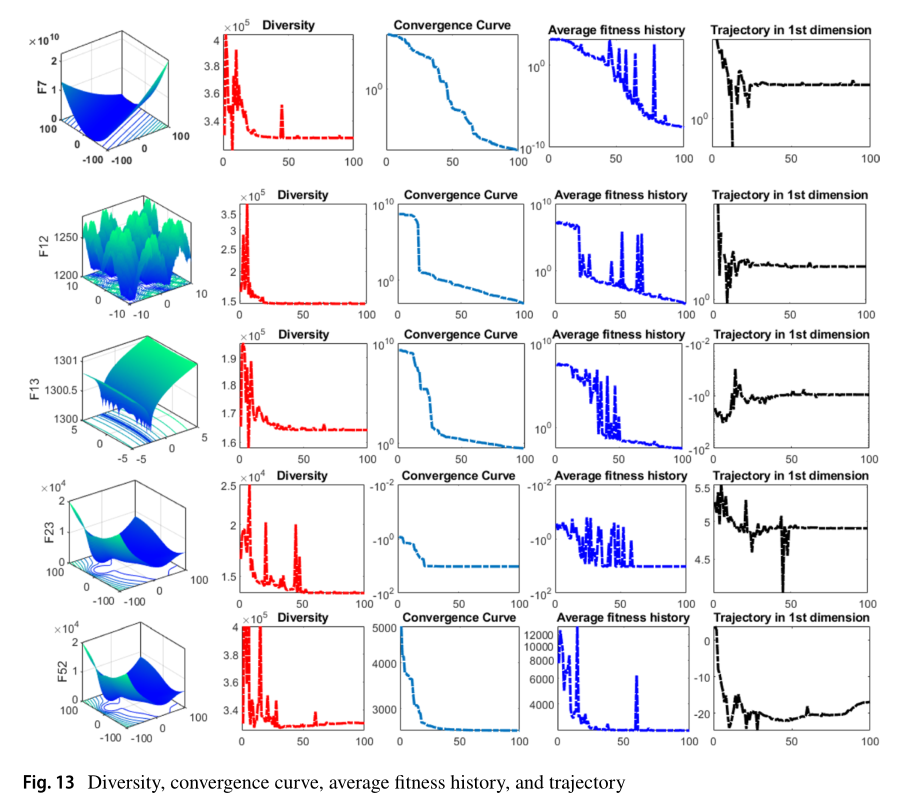
03.论文中算法对比图
04.部分代码
function [Best_score,Best_SW,Convergence_curve]=SWO(SearchAgents_no,Tmax,lb,ub,dim,feval)
%%%%-------------------Definitions--------------------------%%
%%
Best_SW=zeros(1,dim); % A vector to include the best-so-far spider wasp(Solution)
Best_score=inf; % A Scalar variable to include the best-so-far score
Convergence_curve=zeros(1,Tmax);
ub = ub*ones(1,dim);
lb = lb*ones(1,dim);
%%-------------------Controlling parameters--------------------------%%
%%
TR=0.3; %% Representing the trade-off probability between hunting and mating behaviours.
Cr=0.2; %% The Crossover probability
N_min=20; %% Representing the minimum population size.
%%---------------Initialization----------------------%%
%%
Positions=initialization(SearchAgents_no,dim,ub,lb); % Initialize the positions of spider wasps
t=0; %% Function evaluation counter
%%---------------------Evaluation-----------------------%%
for i=1:SearchAgents_no%% Test suites of CEC-2014, CEC-2017, CEC-2020, and CEC-2022SW_Fit(i)=feval(Positions(i,:)');% Update the best-so-far solutionif SW_Fit(i)<Best_score % Change this to > for maximization problemBest_score=SW_Fit(i); % Update the best-so-far scoreBest_SW=Positions(i,:); % Update te best-so-far solutionend
end
% Main loop
while t<Tmax%%a=2-2*(t/Tmax); % a decreases linearly from 2 to 0a2=-1+-1*(t/Tmax); % a2 linearly dicreases from -1 to -2 to calculate l in Eq. (8)k=(1-t/Tmax); %% k decreases linearly from 1 to 0 (Eq. (13))JK=randperm(SearchAgents_no); %% A randomly-generated permutation of the search agent's indices if rand<TR %% 3.2 Hunting and nesting behavior% Update the Position of search agentsfor i=1:SearchAgents_nor1=rand(); % r1 is a random number in [0,1]r2=rand(); % r2 is a random number in [0,1]r3=rand(); % r3 is a random number in [0,1]p = rand(); % p is a random number in [0,1]C=a*(2*r1-1); % Eq. (11) in the paperl=(a2-1)*rand+1; % The parameter in Eqs. (7) and (8)L=Levy(1); %% L is a Levy-based number vc = unifrnd(-k,k,1,dim); %% The vector in Eq. (12)rn1=randn; %% rn1 is a normal distribution-based number %%O_P=Positions(i,:); %% Storing the current position of the ith solution%%for j=1:size(Positions,2)if i<k*SearchAgents_noif p<(1-t/Tmax) %% 3.2.1 Searching stage (Exploration)if r1<r2m1=abs(rn1)*r1; %% Eq. (5)Positions(i,j)=Positions(i,j)+m1*(Positions(JK(1),j)-Positions(JK(2),j)); %% Eq. (4)elseB=1/(1+exp(l)); %% Eq. (8)m2=B*cos(l*2*pi); %% Eq. (7) Positions(i,j)=Positions(JK(i),j)+m2*(lb(j)+rand*(ub(j)-lb(j))); %% Eq. (6)end %% End Ifelse %% 3.2.2 Following and escaping stage (exploration and exploitation)if r1<r2Positions(i,j)=Positions(i,j)+C*abs(2*rand*Positions(JK(3),j)-Positions(i,j)); %% Eq. (10)elsePositions(i,j)=Positions((i),j).*vc(j); %% Eq. (12)end %% End Ifendelseif r1<r2Positions(i,j)=Best_SW(j)+cos(2*l*pi)*(Best_SW(j)-Positions(i,j)); % Eq. (16)elsePositions(i,j)=Positions(JK(1),j)+r3*abs(L)*(Positions(JK(1),j)-Positions(i,j))+(1-r3)*(rand>rand)*(Positions(JK(3),j)-Positions(JK(2),j)); % Eq. (17)end %% End ifend %% End ifend %% End Inner If%% Return the search agents that exceed the search space's boundsfor j=1:size(Positions,2)if Positions(i,j)>ub(j)Positions(i,j)=lb(j)+rand*(ub(j)-lb(j));elseif Positions(i,j)<lb(j)Positions(i,j)=lb(j)+rand*(ub(j)-lb(j));endend SW_Fit1=feval(Positions(i,:)'); %% The fitness value of the newly generated spider% Memory Saving and Updating the best-so-far solutionif SW_Fit1<SW_Fit(i) % Change this to > for maximization problemSW_Fit(i)=SW_Fit1; % Update the local best fitness% Update the best-so-far solutionif SW_Fit(i)<Best_score % Change this to > for maximization problemBest_score=SW_Fit(i); % Update best-so-far fitnessBest_SW=Positions(i,:); % Update best-so-far positionendelsePositions(i,:)=O_P; %% Return the last best solution obtained by the ith solutionendt=t+1;if t>Tmaxbreak;endConvergence_curve(t)=Best_score;end %% Enter Outer For%% Mating behaviorelse % Update the Position of search agentsfor i=1:SearchAgents_nol=(a2-1)*rand+1; %% The parameter in Eqs. (7) and (8)SW_m=zeros(1,dim); %% including the spider wasp maleO_P=Positions(i,:); %% Storing the current position of the ith solution%% The Step sizes used to generate the male spider with a high quality if SW_Fit(JK(1))<SW_Fit(i) %Eq. (23)v1=Positions(JK(1),:)-Positions(i,:); elsev1=Positions(i,:)-Positions(JK(1),:);endif SW_Fit(JK(2))<SW_Fit(JK(3)) %Eq. (24)v2=Positions(JK(2),:)-Positions(JK(3),:);elsev2=Positions(JK(3),:)-Positions(JK(2),:);end%%rn1=randn; %% rn1 is a normal distribution-based number rn2=randn; %% rn1 is a normal distribution-based number for j=1:size(Positions,2)SW_m(j)= Positions(i,j)+(exp(l))*abs(rn1)*v1(j)+(1-exp(l))*abs(rn2)*v2(j); % Eq. (22)if(rand<Cr) %% Eq. (21)Positions(i,j)=SW_m(j);endend%% Return the search agents that exceed the search space's boundsfor j=1:size(Positions,2)if Positions(i,j)>ub(j)Positions(i,j)=lb(j)+rand*(ub(j)-lb(j));elseif Positions(i,j)<lb(j)Positions(i,j)=lb(j)+rand*(ub(j)-lb(j));endend SW_Fit1=feval( Positions(i,:)');%% The fitness value of the newly generated spider% Memory Saving and Updating the best-so-far solutionif SW_Fit1<SW_Fit(i) % Change this to > for maximization problemSW_Fit(i)=SW_Fit1; % Update the local best fitness% Update the best-so-far solutionif SW_Fit(i)<Best_score % Change this to > for maximization problemBest_score=SW_Fit(i); % Update best-so-far fitnessBest_SW=Positions(i,:); % Update best-so-far positionendelsePositions(i,:)=O_P; %% Return the last best solution obtained by the ith solutionendt=t+1;if t>Tmaxbreak;endConvergence_curve(t)=Best_score;end %% End Forend %% End If%% Population reduction %%SearchAgents_no=fix(N_min+(SearchAgents_no-N_min)*((Tmax-t)/Tmax)); %% Eq. (25)
end %% End While
Convergence_curve(t-1)=Best_score;
end
% Draw n Levy flight sample
function L=Levy(d)
beta=3/2;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;
v=randn(1,d);
step=u./abs(v).^(1/beta);
L=0.05*step;
end05.本代码效果图
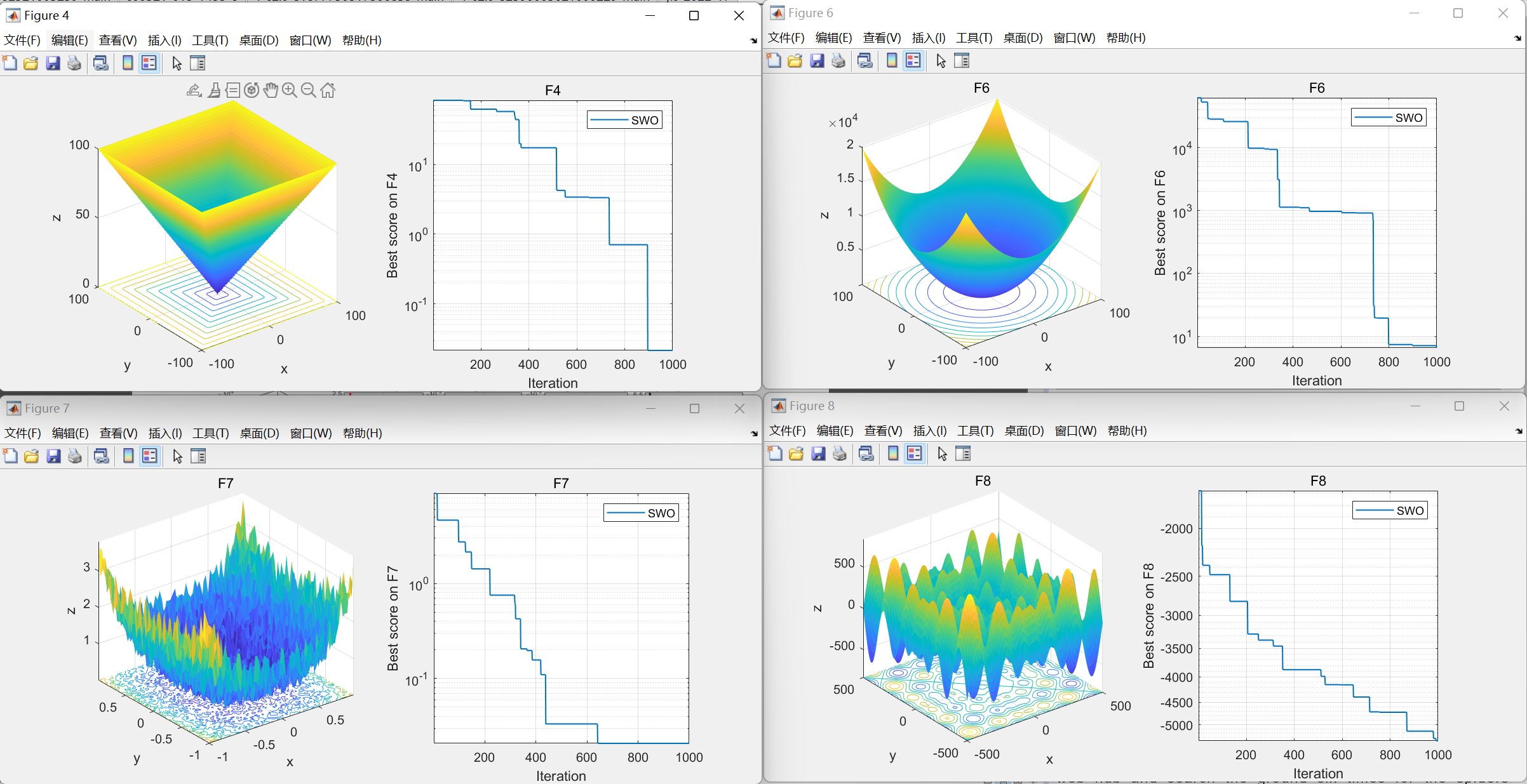
获取代码请关注MATLAB科研小白的个人公众号(即文章下方二维码),并回复智能优化算法本公众号致力于解决找代码难,写代码怵。各位有什么急需的代码,欢迎后台留言~不定时更新科研技巧类推文,可以一起探讨科研,写作,文献,代码等诸多学术问题,我们一起进步。
这篇关于【智能优化算法】蛛蜂优化算法(Spider Wasp Optimizer,SWO)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




