相位解包裹（二）相位解包裹的难处

本文主要是介绍相位解包裹（二）相位解包裹的难处，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

上一篇文章讲了一维相位解包裹，Itoh方法可以总结为 ：连续相位可以通过累加截断相位的差值的截断而求得，也就是表示为下面的式子

从理论和逻辑上看，一维相位解包裹都不复杂，这里就接着上文，讨论从一维推广到二维相位解包裹，到底出了什么问题导致这个问题变得至今都没有完美的解决方法。

 

二维相位解包裹

根据Itoh方法，可以将一维相位解包裹推广到二维相位解包裹中，可以用以下式子来表示：

式中， 为 点的连续相位， 为起始的点的连续相位， 为相位图中连接点和点的任意路径， 为相位差。

拓展后的Itoh方法，要写成代码的话，逻辑其实和一维的情况是一样的，只是原来只遍历一个一维的矩阵（或者数组），现在变为了二维的矩阵（或数组），具体方法如下：

选取相位图中的某一行（列）作为起始行（列），遍历相位图的每一行（列），比较相邻两个点的相位值，若相邻两点的相位差大于 pi，则后一个点的相位加2pi ；若相邻两点的相位差小于-pi ，则后一个点的相位减2pi ；若相邻两点的相位差大于-pi且小于pi ，则不需要进行操作直接比较下一个位置。

 

二维相位解包裹路径问题

从二维相位解包裹的式子中可以看出来，这一个路径积分要保证每一次算出来的点连续相位都一样，那就应该是一个与路径无关的计算过程。但是在实际的相位解包裹的过程中可以发现，选择了不同的路径，往往得到的相位值也不一样，这是实际获取的相位图存在采样率不足导致的相位混叠、获取过程中引入的相位噪声、奇异点等因素导致的，这也导致了正确的二维相位解包裹，是一个与路径有关的问题。

正是因为解包裹过程与路径有关的问题，导致二维相位解包裹变得困难。

为了解决与路径有关的问题，相位解包裹其中一个大类也因此诞生了，空间（空域）相位解包裹（Spatial phase unwrapping），这类方法就是通过选择一条最优的路径去完成全图相位解包裹的，不过这留到以后的文章慢慢讲了。

 

一些小实验

在这篇文章的最后，想放一些很久以前我做过的实验来说明一下，相位混叠、噪声、奇异点等因素会对相位解包裹带来怎样的灾难性破坏。实验都是通过FTP提取相位，然后用最简单的逐行（列）遍历去解包裹相位的。

实验1

这是一个铁罐子，对于这种简单的几何物体，恢复出来的相位还是能基本看出物体原来的形状，不过也可以看到边缘的地方噪声导致的相位解包裹错误。

 

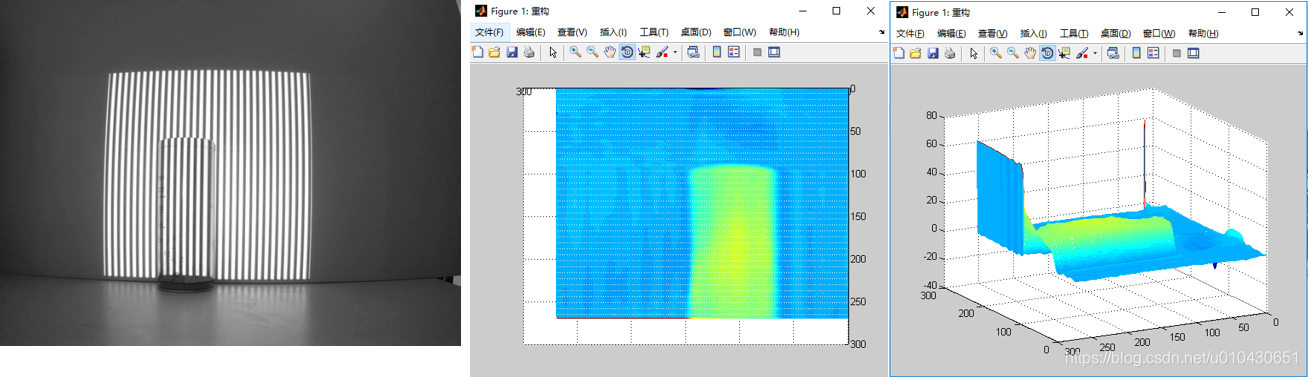
实验2

这是一张卷曲的纸，和上一个实验情况类似，基本能看出纸的形状，边缘也存在解包裹错误。

 

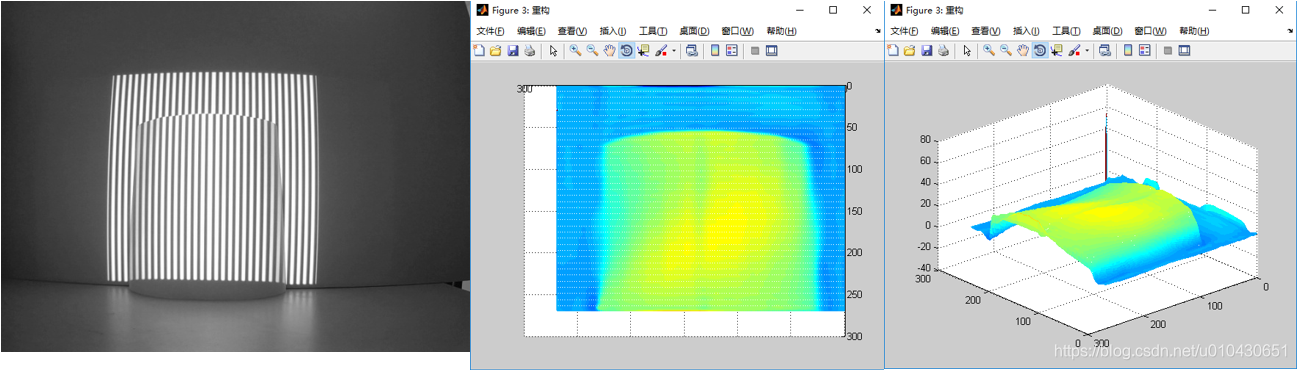
实验3

 这是一个水壶，可以看到图中边缘的部分成片的解包裹错误，这是高度突变，对这一区域采样率不足导致的。

 

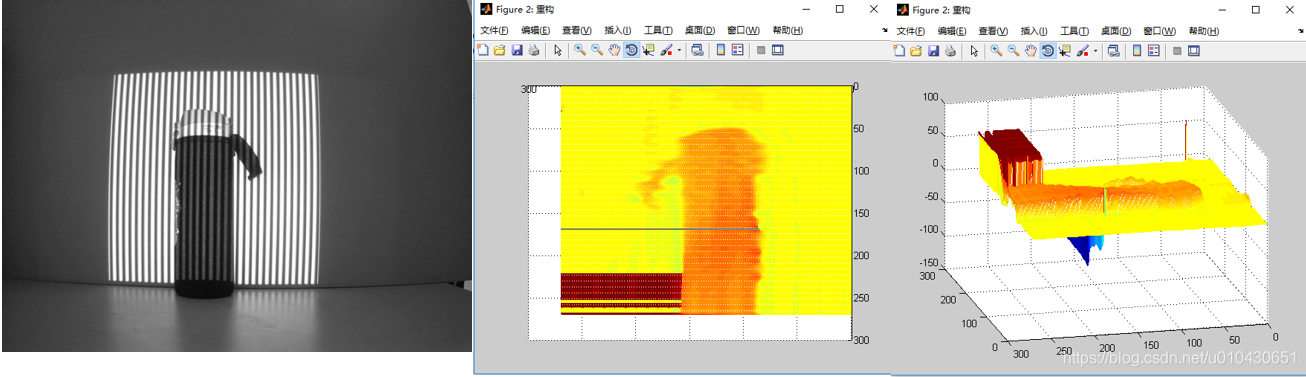
实验4

当测量一些形状更复杂的物体，就可以看出，解包裹后的相位是乱七八糟的。

 从以上实验可以看出来，直接用最简单的方法去相位解包裹，对形状较简单的物体，仍然会存在一些噪声，而对于形状复杂的物体是完全不可行的。

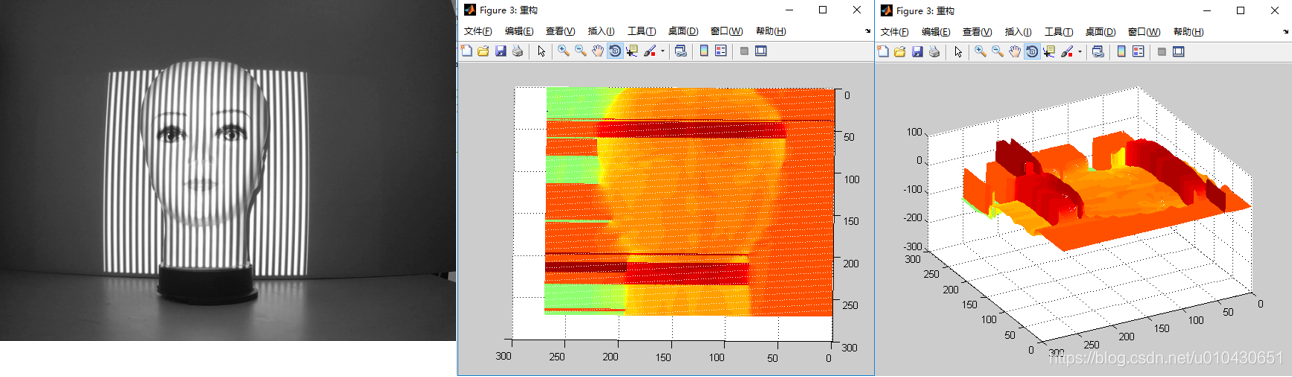
但当采用合适相位解包裹算法，如下图，即使是人脸，也是可以解出来的。因此如何解决相位解包裹与路径有关的问题就非常重要了，不过这就留在后续的文章慢慢讨论了。

 

 

 

 

 

参考文献：

[1] Ghiglia D C, Pritt M D. Two-dimensional phase unwrapping: theory, algorithms, and software[M]. New York: Wiley, 1998.

 

声明：本文中的图片、公式等都和作者本人的毕业论文有关，如果抄袭盗用吃亏是你自己哦~实在有需要，这里建议你自己码一下公式，自己做一下相关的图哦亲。作者水平有限，如文中有错，请务必留言指正。如有学习交流需要，也可通过邮箱zhenyuchung@m.scnu.edu.cn联系我，大家一起讨论学习。

这篇关于相位解包裹（二）相位解包裹的难处的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---