信号处理中的相位

本文主要是介绍信号处理中的相位，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

相位

用来描述波动或振动状态。
在信号处理和通信领域，相位通常指的是信号相对于某一参考信号的延迟。
在周期性信号中，相位通常以角度（弧度或度）来表示，表示信号的周期性变化相对于参考信号的位置。
在非周期性信号中，相位可以是一个复数，其中的实部表示信号的幅度，虚部表示相位信息。
在数字信号处理中，相位通常用于描述信号的时序特性，如在频率分析中的频率和相位信息。

形象小例子

如果两人同时扔石头，那么A的波浪和B的波浪将会同步，即它们的波峰和波谷会重叠。这时我们说两个波的相位相同。但如果A稍微延迟一下再扔石头，A的波浪就会落后于B的波浪，波峰和波谷之间就不再完全重叠，这时我们说两个波的相位不同，A的波浪相对于B的波浪有了一定的相位差。
在信号处理中，相位也是描述波动状态的，只不过这里的波动是指电磁波或者其他类型的信号。通过了解信号的相位，我们可以知道不同信号之间的时间关系，进而帮助我们分析和处理这些信号。

计算与表示

对于正弦波或余弦波等简单周期信号，相位可以通过信号的周期性特征来计算。例如，正弦波的相位可以用角度表示，相位为0度时表示波形在最高点，相位为90度时表示波形在零点，以此类推。

对于复杂的非周期离散时间信号，可以使用离散傅里叶变换（DFT）或快速傅里叶变换（FFT）将信号转换到频率域，然后通过计算每个频率分量的相位来获取信号的相位信息。
在复数表示中，一个复数可以用实部和虚部表示。设一个复数为z，实部为a，虚部为b，则复数z可以表示为z = a + bi，其中i是虚数单位，满足i² = -1。这种表示方式称为直角坐标形式。

对于复数z = a + bi，可以使用反正切函数来计算其相位。相位（或幅角）通常用θ表示，计算公式为：

θ = arctan(b/a)

其中，arctan是反正切函数，b是虚部，a是实部。

需要注意的是，直接使用反正切函数计算相位时，会存在一些问题。例如，当a为0时，即实部为0时，直接计算arctan(b/0)会导致无法定义的结果。因此，在实际应用中，通常会使用带符号的反正切函数（atan2函数），该函数可以正确地计算任意复数的相位，并返回一个[-π, π]（或[-180°, 180°]）范围内的结果。

相位如何反应时间信息

相位在信号处理中反映了信号的时间信息，特别是在周期性信号中，相位差表示不同信号在时间上的先后关系。以下是相位反映时间信息的几种常见方式：

相位与时间延迟的关系：

对于周期性信号，如正弦波或余弦波，相位差可以直接转换为时间延迟。例如，对于频率为f的正弦波信号，若两个信号之间的相位差为Δθ，则时间延迟Δt可以通过下式计算：
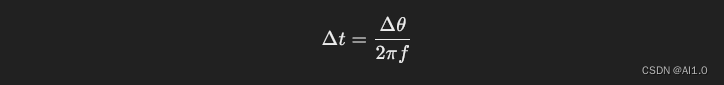这里，Δθ是以弧度表示的相位差，f是信号的频率。

相位速度（相位速度与时间的关系）：

相位速度是波传播速度的一种，表示相同相位点（例如波峰）随时间移动的速度。相位速度vp与波长λ和频率f的关系为：
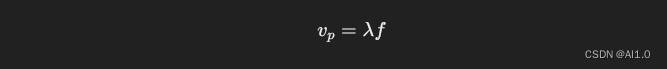如果知道相位速度和波长，可以确定信号的时间延迟和相位差。

复数信号的相位与时间信息：

对于复数信号（如用傅里叶变换处理后的频域信号），信号的相位可以表示为复数的幅角。通过复数的实部和虚部计算相位，再结合频率信息，可以反映信号在时间上的特性。例如，一个频域信号的相位差可以表示不同频率分量在时间上的延迟差异。

信号相干和相位同步：

在通信系统中，相位同步是确保发送和接收信号在相位上保持一致的重要过程。通过相位同步，可以消除或减少信号传输中的时间延迟，确保信号的正确解调。

实例：正弦波信号的相位差与时间延迟

假设有两个正弦波信号，频率为50 Hz，分别为：

x1(t)=sin⁡(2π⋅50t)
x2(t)=sin⁡(2π⋅50t+π/4)

信号x2相对于信号x1有一个π/4的相位差。对应的时间延迟Δt可以通过上述公式计算：
这表明信号x2相对于信号x1有0.0025秒的时间延迟。

通过这些计算和概念，可以看出相位在描述和分析信号的时间特性方面的重要性。

这篇关于信号处理中的相位的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---