本文主要是介绍【FPGA数字信号处理】并行FIR滤波器,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在数字信号处理领域,FIR(Finite Impulse Response)数字滤波器是一种非常重要的工具。它具有线性相位、稳定性好等优点,被广泛应用于通信、音频处理、图像处理等领域。
今天介绍一下并行 FIR 数字滤波器的原理以及实现。
一、FIR数字滤波器原理解析
1、数字滤波器
数字滤波器是数字信号处理领域的核心组件,它们对信号进行数学处理以增强或抑制某些特性。
数字滤波器按照其结构设计可分为两大类:有限冲激响应(FIR)和无限冲激响应(IIR)滤波器。
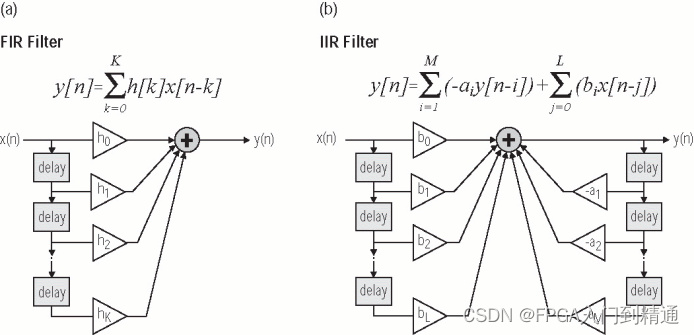
FIR滤波器以其线性相位和较高的资源消耗而闻名;而IIR滤波器则以非线性相位和较低的资源消耗为特点。
线性相位:表示信号的相位变化呈现线性关系,从而保障了信号的时延特性得到精确的保持。
非线性相位:不同频率成分的信号在输入时保持的相对相位差,通过线性相位系统处理后,这些相对相位差仍然保持不变。
对于相位信息敏感的应用场景,如调制和解调过程,需要使用FIR滤波器;
对于关注特定频率成分的应用场景,不关心相位信息,比如单一频率成分的提取,为了优化资源使用,可以优先考虑IIR滤波器。
2、FIR数字滤波器
有限冲激响应(FIR)滤波器因其稳定性、线性相位特性以及无反馈结构而广受欢迎。
FIR 数字滤波器是一种离散时间系统,其输出信号是输入信号与滤波器系数的线性卷积。对于一个长度(抽头数)为 N 、阶次为N-1的 FIR 滤波器,其输入信号为 x(n),输出信号为 y(n),则有:
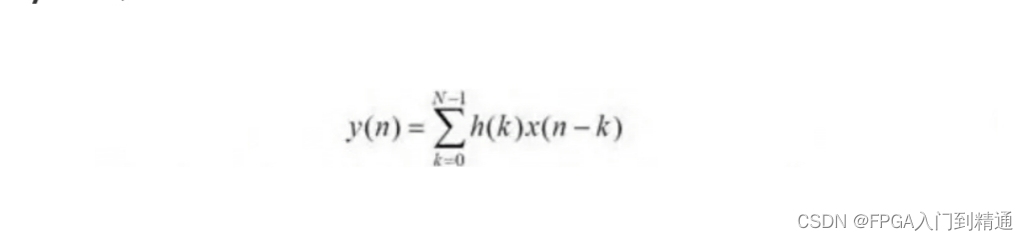
其中,h(k)是滤波器系数。
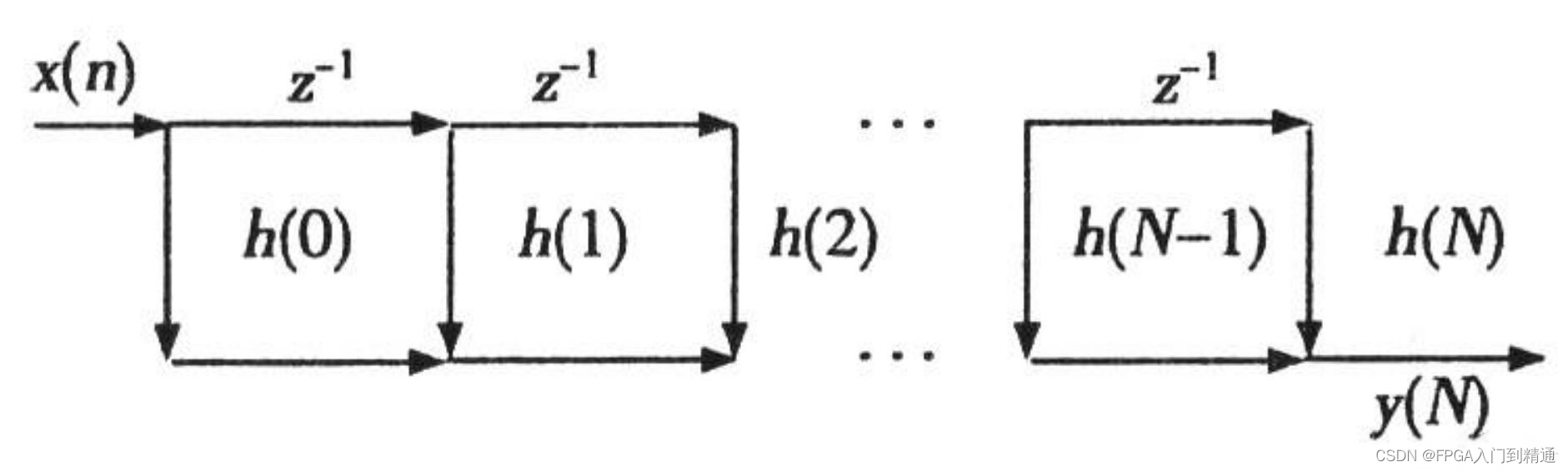
从公式中,可以看出,完成一次滤波运算需要N次乘法和N−1次加法。
FIR滤波器常见的实现结构有直接型、级联型、频率取样型等,其中“直接型”结构适合FPGA实现,也就是直接由卷积公式得到。
3、并行FIR滤波器
(1)结构特点
由多个处理单元同时对输入信号进行处理。每个处理单元通常对应一个滤波器系数,输入信号同时与各个系数相乘,然后将乘积结果累加得到输出。
可以采用多个乘法器和加法器并行工作,以提高处理速度。
(2)性能优势
处理速度快。由于多个处理单元同时工作,可以在较短的时间内完成对输入信号的滤波处理。
适合高速实时信号处理应用,如高速数据通信、图像处理等领域。
(3)实现难点
硬件资源消耗较大。
需要多个乘法器和加法器,以及相应的控制逻辑,这会增加硬件成本和设计复杂度。
二、Python计算滤波器系数
1、FIR滤波器设计示例
设计一个2kHz采样,500Hz截止的15阶低通滤波器(h(n)长度为16),过渡带500~600Hz的FIR滤波器,量化位数为12bit,输入信号位宽也为12bit。
2、Python代码
from scipy.signal import firwin, freqz
import numpy as np
import matplotlib.pyplot as plt# 设计参数
fs = 2000 # 采样频率2kHz
cutoff = 500 # 截止频率500Hz
transition_width = 100 # 过渡带宽500Hz到600Hz
numtaps = 16 # 滤波器阶数15,加上直流项,总共16个系数
quantization_bits = 12 # 量化位数12bit# 设计FIR低通滤波器
h = firwin(numtaps, cutoff, fs=fs, window='hamming', pass_zero='lowpass')# 量化滤波器系数
quantized_h = np.round(h * (2**quantization_bits - 1)).astype(int)# 频率响应
w, h_freq = freqz(h, worN=8000)
w_quantized, h_freq_quantized = freqz(quantized_h, worN=8000)# 绘制滤波器频率响应
plt.figure(figsize=(12, 6))
plt.plot(0.5*fs*w/np.pi, np.abs(h_freq), 'b', label='原始滤波器响应')
plt.plot(0.5*fs*w_quantized/np.pi, np.abs(h_freq_quantized), 'r', label='量化后滤波器响应')
plt.axvline(cutoff, color='k', linestyle='--', label='截止频率')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅度')
plt.title('15阶低通滤波器的频率响应')
plt.legend()
plt.grid()
plt.show()# 返回量化后的滤波器系数
quantized_h.tolist()
3、实现效果
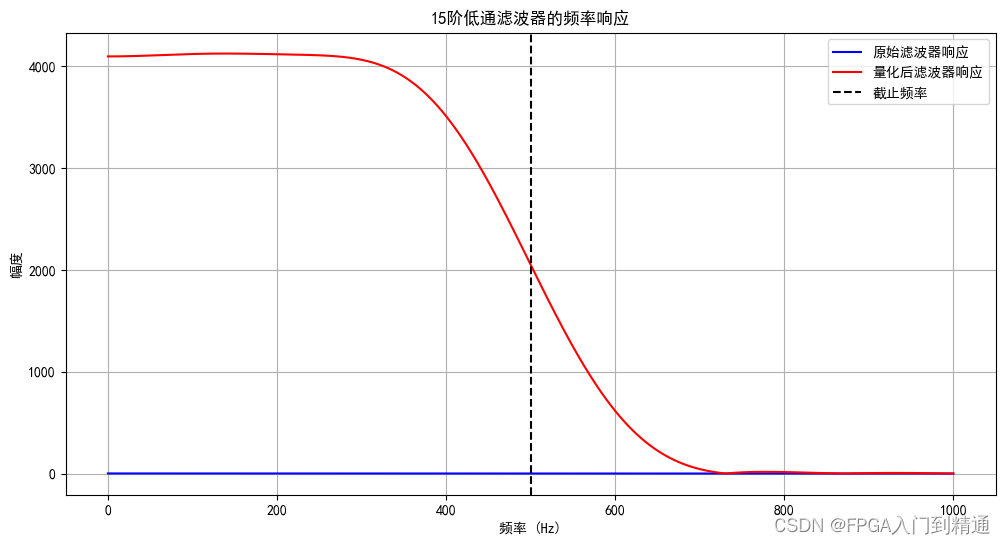
滤波器系数:
-10, -17, 39, 82, -155, -285, 562, 1831, 1831, 562, -285, -155, 82, 39, -17, -10
上图为滤波器的频率响应,蓝色曲线表示原始滤波器响应,红色曲线表示量化后的滤波器响应。黑色虚线表示截止频率。
三、FPGA实现
1、确定滤波器参数
(1)选择滤波器的类型,如低通、高通、带通等,以满足特定的信号处理需求。
(2)确定滤波器的阶数,阶数越高,滤波效果通常越好,但也会增加计算复杂度和硬件资源需求。
(3)确定滤波器的系数,这些系数决定了滤波器的频率响应特性。可以通过理论计算、设计工具或实验调整来确定合适的系数。
2、FPGA设计关键逻辑
从Python中计算FIR滤波器系数是对称的,16个滤波器系数只需要8个乘法器即可。
同时将输入系数与滤波器系数相乘,最后计算总和即可得滤波信号。
总的计算逻辑不复杂,需要注意的是有符号数运算。
篇幅限制,后续再补充代码。

如果需要更多学习资料和源码,想要学习FPGA实战入门进阶,请阅读下面这篇文章:
FPGA入门真的难吗?少走弯路,少踩坑。
这篇关于【FPGA数字信号处理】并行FIR滤波器的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



