本文主要是介绍Good Bye 2014 B. New Year Permutation 并查集 最短路 floyed算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
User ainta has a permutation p1, p2, ..., pn. As the New Year is coming, he wants to make his permutation as pretty as possible.
Permutation a1, a2, ..., an is prettier than permutation b1, b2, ..., bn, if and only if there exists an integer k (1 ≤ k ≤ n) wherea1 = b1, a2 = b2, ..., ak - 1 = bk - 1 and ak < bk all holds.
As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n, i ≠ j) if and only ifAi, j = 1.
Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.
The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.
The second line contains n space-separated integers p1, p2, ..., pn — the permutation p that user ainta has. Each integer between 1and n occurs exactly once in the given permutation.
Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of thei-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0 holds.
In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.
7 5 2 4 3 6 7 1 0001001 0000000 0000010 1000001 0000000 0010000 1001000
1 2 4 3 6 7 5
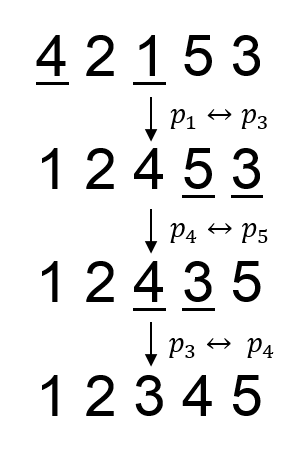
5 4 2 1 5 3 00100 00011 10010 01101 01010
1 2 3 4 5
In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).
In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4).
A permutation p is a sequence of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. Thei-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.
首先给一个简单的想法,如果知道任意两点是否可以交换(包括间接交换),那么,我们只需要从最小的数开始一个一个的确定最小的位置 ,就可以得出答案了。如果要知道间接是否可交换,相当于求,任意两点间,最短路是否可为1,用floyed算法求出,复杂度为o(n ^3)
#define N 305
#define M 100005
#define maxn 205
#define MOD 1000000000000000007
int n,b[N][N],p[N],a[N];
char str[N];
void prin(){FI(n)if(!i)printf("%d",p[i] + 1);elseprintf(" %d",p[i] + 1);printf("\n");
}
int main()
{//freopen("in.txt", "r", stdin);//freopen("out.txt", "w", stdout);while(S(n)!=EOF){FI(n) {S(p[i]);p[i]--;a[p[i]] = i;}FI(n) {SS(str);for(int j = 0;str[j] != '\0';j++){b[i][j] = str[j] == '1'?1:0;}}for(int i = 0;i<n;i++)for(int j = 0;j<n;j++)for(int k = 0;k<n;k++){b[j][k] = max(b[j][k],b[j][i] & b[i][k]);}FI(n){for(int j = 0;j<a[i];j++){if(p[j] > i && b[a[i]][j]){int t = p[j],t2 = a[i];p[j] = i;p[t2] = t;a[i] = j;a[t] = t2;break;}}}prin();}//fclose(stdin);//fclose(stdout);return 0;
}第二种方法。用并查集优化,由于,在同一个集合内的点,明显,只需要从小到大排(因为同一集合,经过一点变换,一定可以生成各种排列),就一定是最优解了。复杂度,为O(n * n);
#define N 305
#define M 100005
#define maxn 205
#define MOD 1000000000000000007
int n,p[N],num[N];
char str[N];
vector<int> g[N];
struct UnionFind{int fa[N];int findFa(int x){return fa[x] == x? x:fa[x] = findFa(fa[x]);}void init(int n){FI(n) fa[i] = i;}void Uni(int a,int b){fa[findFa(a)] = findFa(b);}
}U;
int main()
{//freopen("in.txt", "r", stdin);//freopen("out.txt", "w", stdout);while(S(n)!=EOF){U.init(n);fill(num,0);FI(n) {S(p[i]);p[i]--;}FI(n) {SS(str);for(int j = 0;str[j] != '\0';j++){if(str[j] == '1'){U.Uni(i,j);}}}FI(n) g[U.findFa(i)].push_back(p[i]);FI(n) if(U.findFa(i) == i) sort(g[i].begin(),g[i].end());FI(n){int fa = U.findFa(i);int t = g[fa][num[fa]++];if(!i) printf("%d",t + 1);else printf(" %d",t + 1);}printf("\n");}//fclose(stdin);//fclose(stdout);return 0;
}
这篇关于Good Bye 2014 B. New Year Permutation 并查集 最短路 floyed算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







