[GESP样题 四级] 填幻方和幸运数

本文主要是介绍[GESP样题 四级] 填幻方和幸运数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

B3940 [GESP样题 四级] 填幻方

题目

在一个N×N 的正方形网格中，每个格子分别填上从 1 到 N×N 的正整数，使得正方形中任一行、任一列及对角线的几个数之和都相等，则这种正方形图案就称为“幻方”（输出样例中展示了一个3×3 的幻方）。我国古代称为“河图”、“洛书”，又叫“纵横图”。幻方看似神奇，但当 N 为奇数时有很方便的填法：

1. 一开始正方形中没有填任何数字。首先，在第一行的正中央填上 1。
2. 从上次填数字的位置向上移动一格，如果已经在第一行，则移到同一列的最后一行；再向右移动一格，如果已经在最右一列，则移动至同一行的第一列。如果移动后的位置没有填数字，则把上次填写的数字的下一个数字填到这个位置。
3. 如果第 2 步填写失败，则从上次填数字的位置向下移动一格，如果已经在最下一行，则移到同一列的第一行。这个位置一定是空的（这可太神奇了！）。把上次填写的数字的下一个数字填到这个位置。
4. 重复 2、3 步骤，直到所有格子都被填满，幻方就完成了！

快来编写一个程序，按上述规则，制作一个N×N 的幻方吧。

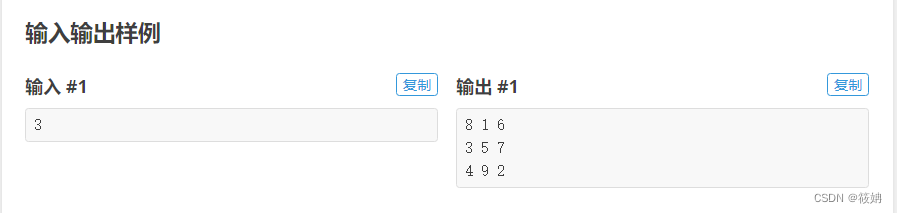
输入为一个正奇数 N，保证 3≤N≤21。

输出 N 行，每行 N个空格分隔的正整数，内容为N×N 的幻方。

运行代码

#include <iostream>  
#include <vector>  
using namespace std;    
void FN(int N) {  vector<vector<int>> FF(N, vector<int>(N, 0));  int num = 1;  int r = 0, c = N / 2;  while (num <= N * N) {  // 将数字填入当前位置  FF[r][c] = num++;  // 计算下一个位置  int R= (r - 1 + N) % N;  int C = (c + 1) % N;  // 检查下一个位置是否已被占用  if (FF[R][C] != 0) {  r = (r+ 1) % N;  } else {  r = R;  c = C;  }  }  // 打印幻方  for (int i = 0; i < N; ++i) {  for (int j = 0; j < N; ++j) {  cout << FF[i][j] << (j < N - 1 ? " " : "\n");  }  }  
}  
int main() {  int N;  cin >> N;  if (N % 2 == 0 || N < 3 || N > 21) {  return 1;  }  FN(N);  return 0;  
}

思路

• 初始化一个N x N的二维向量vector<vector<int>> FF(N, vector<int>(N, 0));，用来存储幻方数据，初始值全为0。设置计数器num = 1，用于填充数字。
• 定义两个变量r和c来追踪当前填充的位置，初始位置设在中心(r = 0, c = N / 2)。
• 使用while循环，直到所有数字填充完毕(num <= N * N)。
• 在当前位置(r, c)放入数字num，然后递增num。
• 计算下一个位置的行R和列C，使用取模运算保证位置在矩阵范围内。
• 如果下一个位置已占用，则向下一行移动；否则，更新当前位置为计算出的下一个位置。

B3850 [GESP202306 四级] 幸运数

题目

小明发明了一种 "幸运数"。一个正整数，其偶数位不变（个位为第 1 位，十位为第 2 位，以此类推），奇数位做如下变换：将数字乘以 7，如果不大于 9 则作为变换结果，否则把结果的各位数相加，如果结果不大于 9 则作为变换结果，否则（结果仍大于 9）继续把各位数相加，直到结果不大于 9，作为变换结果。变换结束后，把变换结果的各位数相加，如果得到的和是 8 的倍数，则称一开始的正整数为幸运数。

例如,16347：第 1位为 7，乘以 7 结果为 49，大于 9，各位数相加为13，仍大于9，继续各位数相加，最后结果为4；第3 位为3，变换结果为3；第 55 位为 1，变换结果为 7。最后变化结果为 76344，对于结果76344 其各位数之和为24，是 8的倍数。因此 16347 是幸运数。

输入第一行为正整数 N，表示有 N个待判断的正整数。约定 1≤N≤20。从第 2 行开始的 N 行，每行一个正整数，为待判断的正整数。约定这些正整数小于 10^12。

输出 N行，对应 N 个正整数是否为幸运数，如是则输出 'T'，否则输出 'F'。

提示：不需要等到所有输入结束在依次输出，可以输入一个数就判断一个数并输出，再输入下一个数。

运行代码

#include <iostream>  
#include <string>  
#include <algorithm>  
using namespace std; 
int FN(long long num) {  int sum = 0;  while (num > 0) {  sum += num % 10;  num /= 10;  }  return sum;  
}  
// 函数：对奇数位进行变换  
string FF(const string& numStr) {  string result;  for (size_t i = 0; i < numStr.size(); ++i) {  if (i % 2 == 0) { // 偶数位直接添加  result += numStr[i];  } else { // 奇数位进行变换  int digit = numStr[i] - '0';  int t = digit * 7;  while (t> 9) {  t= FN(t);  }  result +=to_string(t);  }  }  return result;  
}  
// 函数：判断是否为幸运数  
bool Number(const string& numStr) {  string t = FF(numStr);  return FN(stoll(t)) % 8 == 0;  
}  
int main() {  int N;  cin >> N;  cin.ignore(); // 忽略可能存在的换行符  while (N--) {  string numStr;  getline(cin, numStr); // 读取一行字符串作为数字  if (Number(numStr)) {  cout << "T" << endl;  } else {  cout << "F" << endl;  }  }  return 0;  
}

思路

• 计算一个数的各位数之和。
• FN：对输入的数字字符串的奇数位进行变换，并返回变换后的字符串。
• Number：判断一个数字字符串是否为幸运数。

在main函数中，我们读取要判断的正整数个数N，然后对每个正整数进行判断并输出结果。注意我们使用getline来读取每行的输入，以正确处理可能包含前导零的情况。此外，我们使用stoll将变换后的字符串转换回long long类型，以计算其各位数之和。

这篇关于[GESP样题 四级] 填幻方和幸运数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---