本文主要是介绍Foundation of Machine Learning 笔记第四部分 —— Generalities 以及对不一致假设集的PAC学习证明，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

注意事项：

这个系列的文章虽然题为书本《Foundation of Machine Learning》的读书笔记，但实际我是直接对书本的部分内容进行了个人翻译，如果这个行为有不妥当的地方，敬请告知。
由于知识面限制，部分名词的翻译可能存在错误，部分难以翻译的名词保留英文原词。为了防止误导大家，在这里声明本文仅供参考。
本文基本翻译自《Foundation of Machine Learning》的2.4节。

正文

在这一部分中，我们将讨论几个与学习相关的重要问题，在前些章节中我们为了便于理解而忽略了。

2.4.1 确定性与随机性

在监督学习的大多数情况下，分布 $D$ 定义在空间 $\mathcal{X}\times\mathcal{Y}$ ，训练数据是一个按照 $D$ 独立同分布地抽取的一个带标签样本集 $S$ ：

S = ((x 1, y 1), \dots (x m, y m)) .

$S=\left((x_1,y_1),\dots(x_m,y_m)\right).$ 学习要解决的问题就是寻找一个假设

h∈H h ∈ H $h \in H$ ，使它只有较小的泛化误差

R (h) = P r (x, y) \sim D [h (x) \neq y] = E (x, y) \sim D [1 h (x) \neq y] .

$R(h)={\rm Pr}_{(x,y)\sim D}[h(x)\neq y]=E_{(x,y)\sim D}[1_{h(x)\neq y}].$ 我们把这种情况称为随机场景 ( stochastic scenario )。在这种情况下，输出的标签是输入的一个概率函数。这种随机场景体现了现实世界中同一个输入对应的标签不唯一的特点。例如，如果我们要基于一个人的身高和体重预测性别，很典型地，这里的标签就不唯一。对于同一组身高、体重，他们对应的性别可能是男性也可能是女性。对于每一组数据，它都有一定的概率被标记为男性 ( 我的理解：我觉得这种随机场景实际上是信息不完备造成的，例如在上面的例子中，身高和体重对于性格的描述是不足够的，这导致了样本集本身是矛盾的。基于这样的样本，不管假设集是怎样的都不可能学习到一个完全正确的 concept )。

在这种场景下，PAC 学习框架自然地拓展出一个新的概念：不可知的 PAC 学习 ( agnostic PAC-learning )。

定义 2.4 不可知 PAC 学习

设 $H$ 为一个假设集。如果存在一个多项式函数 $poly(\cdot,\cdot,\cdot)$ ，使得对于任意 $\epsilon \gt 0$ 、任意 $\delta \gt 0$ 和所有在空间 $\mathcal{X}\times\mathcal{Y}$ 上的分布 $D$ ，下式在任意样本量 $m\ge poly(1/\epsilon,1/\delta,n,size(c))$ 的样本集上成立：

P r S \sim D m [R (h S) - min h \in H R (h) \leq ϵ] \geq 1 - δ . (2.21)

${\rm Pr}_{S\sim D^m}\left[R(h_S)-\min_{h\in H}R(h)\le\epsilon\right]\ge 1-\delta.\tag{2.21}$ 那么

 A $\mathcal{A}$ 是一个不可知 PAC 学习算法。进一步的，如果算法

 A $\mathcal{A}$ 的时间复杂度在

poly(1/ϵ,1/δ,n,size(c)) p o l y ( 1 / ϵ , 1 / δ , n , s i z e ( c ) ) $poly(1/\epsilon,1/\delta,n,size(c))$ 以内，这个算法就称为一个有效的不可知 PAC 学习 ( efficient agnostic PAC-learning ) 算法。

当一个点上的标签能够被一个可观测函数 $f:\mathcal{X}\to \mathcal{Y}$ 唯一地确定的时候，这种场景称为确定性场景 ( deterministic scenario )。在这种情况下，考虑只在输入空间 $\mathcal{X}$ 上的分布 D 就足够了。这样，根据 D 抽取 $(x_1,\dots,x_m)$ ，通过对 $i \in [1,m]$ 使用函数 $f:y_i=f(x_i)$ 获取标签，就能得到训练集。很多学习问题都可以被形式化为这种决定性场景。

在前面几个部分中，为了简便我们都只讨论了确定性场景下的学习问题。但是从这些确定性场景拓展到随机场景的方法还是比较直白的(我的理解：随机性场景和前面假设集不一致的情况是不一样的)。

2.4.2 贝叶斯错误率和噪声

在确定性场景的情况下，存在一个没有泛化误差的目标函数 $f$ 使得： $R(h)=0$ 。在随机情况下，存在一个泛化误差大于 0 但最小的假设。

定义 2.5 贝叶斯错误率

给定一个在空间 $\mathcal{X}\times\mathcal{Y}$ 上的分布 $D$ ，贝叶斯错误率 $R^*$ 被定义为可观测函数 $h:\mathcal{X}\to\mathcal{Y}$ 的泛化误差的下确界：

R * = inf h h measurable R (h) . (2.22)

$R^*=\inf_{h \atop h\text{ measurable}} R(h).\tag{2.22}$ 假如一个假设

h h $h$ 有

R (h) = R^{*}

$R(h)=R^*$ ，那么称

h h $h$ 为贝叶斯假设或者贝叶斯分类器。

通过定义可以知道，在确定性场景的情况下，我们有 $R^*=0$ ，但是在随机性场景的情况下， $R^*\neq 0$ 。显然，贝叶斯分类器 $h_{Bayes}$ 可以使用条件概率定义为 ( 我的疑问：那么如何证明下式的泛化误差是所有分类器的泛化误差的下确界？)：

\forall x \in , h B a y e s (x) = arg max y \in {0, 1} P r [y | x] . (2.23)

$\forall x\in \mathcal{X},\quad h_{Bayes}(x)=\mathop{\arg\max}_{y\in \{0,1\}}\ {\rm Pr}[y|x].\tag{2.23}$

hBayes h B a y e s $h_{Bayes}$ 对于一个样本

x∈ x ∈ X $x \in \mathcal{X}$ 的平均错误率为

min{Pr[0|x],Pr[1|x]} min { P r [ 0 | x ] , P r [ 1 | x ] } $\min\{{\rm Pr}[0|x], {\rm Pr}[1|x]\}$ ，这已经是可能达到的最小误差了。贝叶斯分类器又引出了下面对噪声的定义。

定义 2.6 噪声

给定一个在空间 $\mathcal{X}\times\mathcal{Y}$ 上的分布 $D$ ，点 $x\in \mathcal{X}$ 上的噪声定义为

n o i s e (x) = min {P r [1 | x], P r [0 | x]} . (2.24)

$noise(x)=\min\{{\rm Pr}[1|x],{\rm Pr}[0|x]\}.\tag{2.24}$ 与分布

D D $D$ 相关的平均噪声为

E [n o i s e (x)]

$E[noise(x)]$ 。

因此，平均噪声就是前述的贝叶斯错误率： $noise=E[noise(x)]=R^*$ 。噪声是一个衡量学习任务难度的特征。对于一个点 $x\in\mathcal{X}$ ，如果他的噪声 $noise(x)$ 接近于 1/2，常常称 $x$ 为噪点 ( noisy )。噪点是预测的一个挑战。

2.4.3 估计误差和近似误差

假设集 $h\in H$ 的泛化误差和贝叶斯误差的差可以分解成：

R (h) - R * = (R (h) - R (h *))        estimation + (R (h *) - R *)        approximation, (2.25)

$R(h)-R^*=\underbrace {(R(h)-R(h^*))}_{\text{estimation}}+\underbrace {(R(h^*)-R^*)}_{\text{approximation}},\tag{2.25}$ 这里

h∗ h ∗ $h^*$ 是假设集

H H $H$ 中泛化误差最小的假设，或称为 best-in-class hypothesis。第二项称为近似误差，它描述了

H

$H$ 中的假设的错误率与贝叶斯错误率的接近程度。它是假设集

H H $H$ 的一个特性，量化了

H

$H$ 的丰富度。近似误差是无法获得的，因为通常潜在的分布

D D $D$ 都是未知的。甚至我们假设噪声符合某些条件，估计近似误差仍然很难(我的理解：需要注意这里的误差组成和前些章节中误差构成的区别。在随机场景下，学习问题不存在一个目标 concpet，取代目标假设的是贝叶斯假设，也就是在这里我们想要得到的是贝叶斯假设

h_{B a y e s}

$h_{Bayes}$ 。但就像前面不一致的情况一样，当

hBayes∉H h B a y e s ∉ H $h_{Bayes}\notin H$ 的时候，最佳假设

h∗ h ∗ $h^*$ 的泛化误差

R(h∗) R ( h ∗ ) $R(h^*)$ 也不能保证与贝叶斯假设的误差

R∗ R ∗ $R^*$ 相等，他们之间存在着近似误差—— Approximate error。再之，学习算法选出的只是训练误差最小的假设

h h $h$ ，它的泛化误差

R (h)

$R(h)$ 又与最佳假设的泛化误差

R(h∗) R ( h ∗ ) $R(h^*)$ 有差距，这个差距称为估计误差—— Estimation error。这两项误差构成了学习算法得到的假设的泛化误差与贝叶斯误差的差距)。

$(2.25)$ 的第一项是估计误差，它由被选择的假设 $h$ 确定。它描述了假设 $h$ 与 best-in-class 假设的接近程度。不可知PAC学习的定义也是基于估计误差的。算法 $\mathcal{A}$ 的估计误差，也就是算法在样本集 $S$ 上训练后返回的假设 $h_S$ 的估计误差，有时被限制小于某个由泛化误差决定的项。

例如，用 $h_S^{\text{ERM}}$ 代表经验风险最小化算法——也就是返回经验误差最小的假设 $h_S^{\text{ERM}}$ 的一种算法——返回的假设。那么，上一节中定理2.2给出的泛化上限，或者任意其他在 $sup_{h \in H}\left|R(h)-\hat R(h)\right|$ 上的限制，都能被用来限制经验风险最小化算法的估计误差。实际上，通过重写估计误差的计算公式使得公式中出现 $\hat R(h_S^{\text{ERM}})$ ，并且通过定义得到不等式 $\hat R(h_S^{\text{ERM}})\le \hat R(h^*)$ ，我们可以写出

R (h ERM S) - R (h *) = R (h ERM S) - R ̂ (h ERM S) + R ̂ (h ERM S) - R (h *) \leq R (h ERM S) - R ̂ (h ERM S) + R ̂ (h *) - R (h *) \leq 2 sup h \in H ∣ ∣ R (h) - R ̂ (h) ∣ ∣ . (1) (2) (2.26)

$\begin{align} R(h_S^{\text{ERM}})-R(h^*) &=R(h_S^{\text{ERM}}) - \hat R(h_S^{\text{ERM}})+\hat R(h_S^{\text{ERM}})- R(h^*) \\ &\le R(h_S^{\text{ERM}})-\hat R(h_S^{\text{ERM}}) + \hat R(h^*) -R(h^*) \\ &\le 2\sup_{h\in H}{\left|R(h)-\hat R(h)\right|}.\tag{2.26} \end{align}$

(2.26) ( 2.26 ) $(2.26)$ 的右侧可以通过定理 2.2 限制上限，并且假设集增大而上升，

R(h∗) R ( h ∗ ) $R(h^*)$ 随

|H| | H | $|H|$ 上升而下降，这个上限值也上升。

2.4.4 模型选择

基于前几节的理论结果，在这里我们讨论一些模型选择方法和算法思想。我们假设大小为 $m$ 的样本集 $S$ 的生成是服从独立同分布的，并使用 $\hat R_S(h)$ 代表假设 $h$ 在 $S$ 上的误差，以便清除地表示它与 $S$ 的依赖关系。

虽然定理 2.2 给出的保证只对有限的假设集成立，它已经为我们提供了一些在算法设计上的指导，我们将在下一章中提出，类似的保证在假设集无限的情况下同样存在。这样的结果促使我们对经验误差和复杂度项进行思考，在这里复杂度项是一个关于 $|H|$ 和样本量 $m$ 的一个函数。

从这一点出发，一个只寻求取最小化训练集上的误差的算法，ERM算法

\begin{matrix} (2.27) & h_{S}^{ERM} = \underset{h \in H}{\arg max} {\hat{R}}_{S} (h), \end{matrix}

$h_S^{\text{ERM}}=\mathop{\arg \max}_{h \in H}\hat R_S(h),\tag{2.27}$ 可能不是很成功，因为它忽略了复杂度项。事实上，ERM 算法在实践中的效果经常很差。另外在大多数情况下，ERM算法本身计算量非常大，难以计算。例如，寻找一个在训练样本上误差最小的线性假设是一个关于空间维数的 NP 难问题。

另一种被称为结构风险最小化 ( structural risk minimization, SRM ) 方法从一个有着逐渐增大的样本量的无穷的假设集序列

H 0 \subset H 1 \subset \dots \subset H n \dots (2.28)

$H_0 \subset H_1\subset\cdots\subset H_n\cdots \tag{2.28}$ 之中对每个

Hn H n $H_n$ 寻找 ERM 假设

hERMn h n ERM $h_n^{\text{ERM}}$ 。最终选择的假设是这些 ERM 假设

hERMn h n ERM $h_n^{\text{ERM}}$ 中使得经验误差和复杂度项

complexity(Hn,m) c o m p l e x i t y ( H n , m ) $complexity(H_n,m)$ 加起来最小的那个：

h SRM n = arg min h \in H n, n \in ℕ [R ̂ S (h) + c o m p l e x i t y (H n, m)] . (2.29)

$h_n^{\text{SRM}}=\mathop{\arg\min}_{h \in H_n, n \in \mathbb{N}}\left[ \hat R_S(h)+complexity(H_n,m)\right].\tag{2.29}$

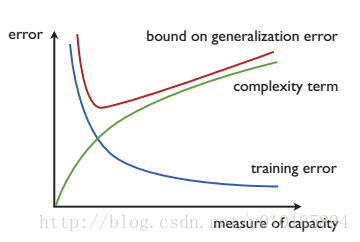
图为结构风险最小化示意图。三种误差被画成了假设集大小的函数。显然，随着假设集大小的上升，训练误差下降，同时复杂度上升。SRM 通过最小化训练误差和复杂度之和，选择使得泛化误差的上限最低的那个假设。

虽然 SRM 从较强的理论保证中受到益处，它的计算往往十分复杂，因为它需要取解多个 ERM 问题的解。注意 ERM 问题的个数不是无限的，因为随着 $n$ 的增大，假设集 $H_n$ 的训练误差变为0，这时因为训练误差不变了，而复杂度项还在不断上升，那么目标函数一定会不断上升，以后后面的假设集就都不用考虑了。

还有另一种基于更加直白的优化策略的算法，这种方法的优化目标函数为经验误差和正则项的和，这个正则项对复杂的假设进行了惩罚。当 $H$ 是一个向量空间的时候，正则项通常被定义为 $h$ 的某种范数 ${||h||^2}$ 通常正则项被定义为某种：

h REG S = arg max h \in H R ̂ S (h) + λ | | h | | 2 . (2.30)

$h_S^{\text{REG}}=\mathop{\arg\max}_{h \in H}\hat R_S(h)+\lambda{||h||}^2.\tag{2.30}$

λ≥0 λ ≥ 0 $\lambda\ge 0$ 是一个正则参数，它可以用来权衡经验误差最小化和复杂度控制之间的比重。在实践中，

λ λ $\lambda$ 通常使用

n n $n$ 折的交叉验证来选择。在下一章中，我们将看到一系列不同的基于正则项的算法。

我的补充

在《Foundation of Machine Learning》的这一节中，作者给出了一个新的定义——不可知 PAC 学习，并且分析了一种更加难的学习问题——随机场景下的学习问题——的误差构成，最后从 PAC 理论作为指导讲述了经验风险最小化和结构风险最小化两种学习模型的原理。

我在阅读书本到这部分的时候，对一些概念的关系的理解比较混乱，于是还查阅了一些其他资料。下面的把查阅到的资料整合起来，企图把这里的体系补充得更加完整。

上文说到随机场景的学习问题这个概念，我们可以把随机场景这类问题纳入到不一致的学习问题当中。把不一致的假设集总结为以下三种：

目标 concept ；
- $c\in H$ ，但是要从 $H$ 中找出 $c$ 是一个难以计算的问题；
- $c$ 不存在。(也就是上文所说的随机情况。我们总是假设存在一个目标 concept 把样本投影到标签中去，但现实中并不总是这样。例如天气预报就没有一个确定的结果，而是给出出现各种天气的概率。我们认为这些问题都是固有随机性的，或者说，这些问题太过复杂以至于以我们现有的知识不能够为它们建立模型。)
显然，上一节的不一致假设学习问题属于第 1, 2 种，这一节引入的随机场景属于第 3 种。
如上文所说的一样，为了研究随机场景下的学习问题，我们引入一种新的形式化方法。我们统一把分布 $D$ 定义在空间 $\mathcal{X} \times \mathcal{Y}$ 中。根据条件概率公式，对于一个样本，我们可以给出：
Pr[(x,y)]=PrD[x]⋅PrD[y|x].
我们可以这么理解分布 D 的样本生成过程，首先按照概率生成样本点，然后由于这一个样本点有可能属于两个或多个标签，那么它就应该还有一个决定样本 x 属于什么标签的概率分布。我们把这种设定下的学习问题的泛化误差定义为：
R(h)=E(x,y)∼D[1h(x)≠y].
经验误差可以定义为：
R̂ (h)=1m∑i=1m1h(xi)≠yi.
我们定义泛化误差最小的分类器为贝叶斯分类器，不知如何得证，下式所示的分类器就是贝叶斯分类器：
∀x∈,hBayes(x)=argmaxy∈{0,1} Pr[y|x].

要注意的是，上面的式子同样可以用到确定的情况下，只是 ${\rm Pr}_D[y|x]$ 被限定为 0 或者 1。所以前一节所说的确定场景下假设集不一致问题同样可以使用这里的方法表达，此时贝叶斯误差 $R^*=0$ 。

由于上一节的定理 2.2 只用到了 Hoeffding 不等式和 Union Bound 进行证明，而改变分布 $D$ 的形式对它们不会造成影响，所以定理 2.2 同样适用在这种设定下的学习问题上。设 $H$ 是一个有限的假设集，那么对于任意 $\delta \gt 0$ ，下面的不等式至少有 $1-\delta$ 的几率成立：

∀h∈H,R(h)≤R̂ (h)+log|H|+log2δ2m‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√.

定理

对于一个有限不一致的假设集 $H$ ，一个从 $H$ 中学习到的经验误差最小的假设 $h_S=\mathop {\arg \min}_{h \in H} \hat R(h)$ ，和任意的 $0\lt\delta \lt 1$ ，下式有 $1-\delta$ 的概率成立：

R(hS)≤2log|H|+log2δ2m‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√+minh∈HR(h).
也就是说，学习问题满足不可知 PAC 学习。

证明因为定理 2.2 成立，由定理 2.2 的推导过程可得对于任意 $\epsilon > 0$ ：

Pr[∃h∈H，|R̂ (h)−R(h)|>ϵ]≤ 2|H|e−2mϵ2.
取反则有：
Pr[∀h∈H，|R̂ (h)−R(h)|≤ϵ]≥ 1−2|H|e−2mϵ2.
若 ∀h∈H, |R̂ (h)−R(h)|≤ϵ 成立，有：
∀h∈H, R(hS)≤≤≤R̂ (hS)+ϵR̂ (h)+ϵR(h)+2ϵ.(3)(4)(5)
其中因为 R(h)−R̂ (h)≤ϵ 对所有 h 成立，第一个不等式成立；因为，第二个不等式成立；因为 R̂ (h)−R(h)≤ϵ 对所有 h 成立，第三个不等式成立。设，解 ϵ ，定理得证。

参考
1. jeremykun 的博客 Occam’s Razor and PAC-learning
2. Princeton Computer Science 511
  Theoretical Machine Learning 的 scribe note 0225