本文主要是介绍Logit Standardization in Knowledge Distillation 知识蒸馏中的logit标准化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
摘要
知识蒸馏涉及使用基于共享温度的softmax函数将软标签从教师转移到学生。然而,教师和学生之间共享温度的假设意味着他们的logits在logit范围和方差方面必须精确匹配。这种副作用限制了学生的表现,考虑到他们之间的能力差异,以及教师天生的logit关系足以让学生学习。为了解决这个问题,我们建议将温度设置为logit的加权标准差,并在应用softmax和KL散度之前进行logit标准化的即插即用Z-score预处理。我们的预处理使学生可以关注教师的基本Logit关系,而不是要求大小匹配,并且可以提高现有基于logit的蒸馏方法的性能。我们还展示了一个典型的例子,其中教师和学生之间的传统共享温度设置不能可靠地产生真实的蒸馏评估;然而,我们的Z-score成功地缓解了这一挑战。
介绍
Hinton等人首先提出通过最小化他们预测之间的KL散度,将教师的知识提炼给学生。这里softmax函数的缩放因子,称为温度T,它的引入是为了软化预测概率。传统上,温度是预先全局设置的超参数,并在整个训练过程中保持固定。CTKD采用对抗学习模块来预测样本温度,以适应不同的样本难度。然而,现有的基于logit的KD方法仍然假设教师和学生应该共享温度,忽略了KL散度中不同温度值的可能性。在这项工作中,我们证明了分类和KD中的一般softmax表达式是从信息论中的熵最大化原理推导出来的。在这个推导过程中,拉格朗日乘数出现,并以温度的形式出现,在此基础上,我们建立了教师和学生的温度之间的不相关性,以及不同样本的温度之间的不相关性。这个证明支持我们在教师和学生之间以及在样本之间分配不同温度的动机。
对比logit预测的精确匹配,发现预测的类间关系足以使学生达到与教师相似的成绩。一个轻量级的学生在预测具有可比范围和方差的对数时面临着与一个笨重的教师相比的挑战。然而,我们证明在KL散度中共享温度的传统做法仍然隐含地强制学生和教师logit之间的精确匹配。现有的基于logit的KD方法没有意识到这个问题,通常会陷入陷阱,导致整体性能下降。为了解决这个问题,我们建议**使用加权logit标准偏差作为自适应温度,并在应用softmax之前将Z-score logit标准化作为预处理步骤。**这种预处理将logit的任意范围映射到有界范围,允许学生logit具有任意范围和方差,同时有效地学习和保留教师logit的固有关系。我们提出了一个典型的案例,其中在softmax中共享温度设置下的KL散度损失可能会产生误导,并且不能可靠地衡量蒸馏学生的表现。相比之下,使用我们的Z-score预处理,在这种情况下消除了共享温度的问题。
贡献
(1)基于信息论中的熵最大化原理,利用拉格朗日乘子导出了基于logit的KD中softmax的一般表达式。我们表明,温度来自于衍生的乘数,允许它被不同的样本和不同的学生和老师选择。
(2)为了解决由共享温度引起的传统基于logit的KD管道的问题,包括隐式强制logit匹配和学生模型不真实的索引。我们提出了一种logit蒸馏的预处理,以自适应地在教师和学生之间以及跨样本分配温度,能够促进现有的基于logit的KD方法。
Background and Notation
我们拥有一个转移数据集D包含所有N样本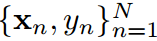 ,这里
,这里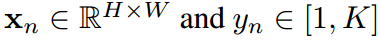 分别是第n个样本的图片和标签。H,W,K是图片的高度、宽度和类的数量。给定一个输入
分别是第n个样本的图片和标签。H,W,K是图片的高度、宽度和类的数量。给定一个输入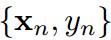 ,教师
,教师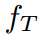 和学生
和学生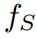 分别预测logit向量
分别预测logit向量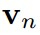 和
和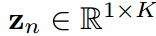 。即
。即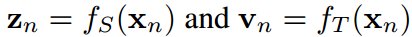 ,
,
人们普遍接受的是,使用涉及温度T的softmax函数将logit转换为概率向量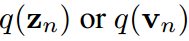 ,使它们的第k项具有:
,使它们的第k项具有:
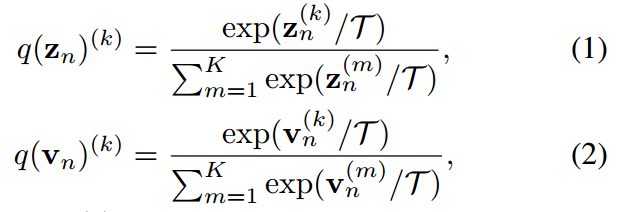
其中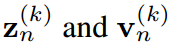 ,分别是
,分别是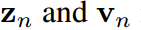 的第k项。知识蒸馏的过程本质上是让
的第k项。知识蒸馏的过程本质上是让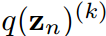 模拟
模拟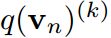 对任何类和所有样本。目标是通过最小化KL散度来实现的。
对任何类和所有样本。目标是通过最小化KL散度来实现的。
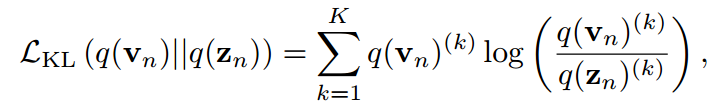
当只对z进行优化时,理论上等于交叉熵损失:
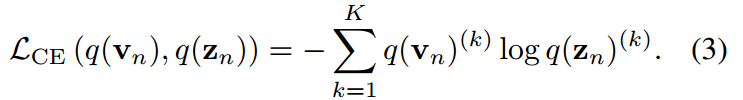
注意,它们在经验上是不等价的,因为它们的梯度由于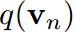 的负熵项而发散。
的负熵项而发散。
方法
温度之间的不相关性
在第4.1.1和4.1.2中,我们首先基于信息论中的熵最大化原理推导了分类和KD中涉及温度的softmax函数。这意味着学生和教师的温度可以是不同的,并且样本明智地不同。
分类中的Softmax推导
可以证明分类中的softmax函数在概率归一化条件下和信息论中状态期望的约束是熵最大的唯一解。该推导在置信度校准中也被利用来制定温度标度。假设我们有如下约束熵最大化优化:
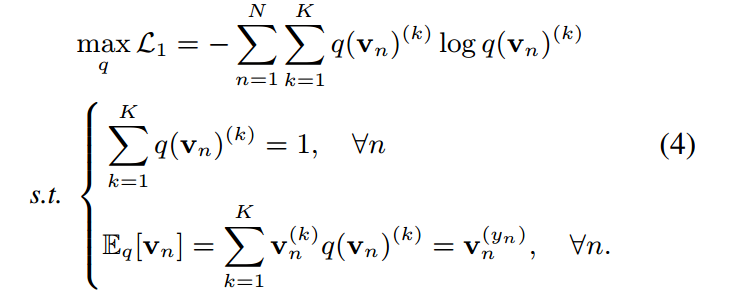
第一个约束由于对离散概率密度的要求而成立,第二个约束控制了分布的范围,使模型能够准确地预测目标类。设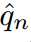 为one-hot硬概率分布,其值除目标指标
为one-hot硬概率分布,其值除目标指标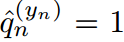 外均为0。第二个约束实际上是
外均为0。第二个约束实际上是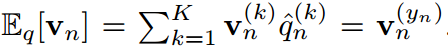 。这相当于使模型预测正确的标签
。这相当于使模型预测正确的标签 。应用拉格朗日乘子
。应用拉格朗日乘子 ,得到:
,得到:
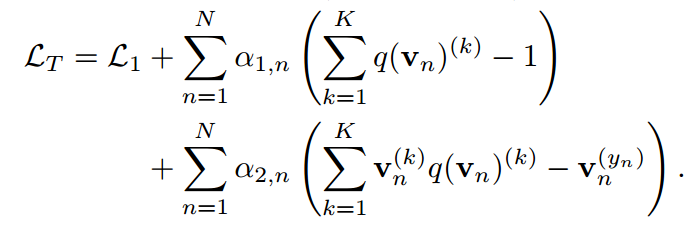
对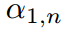 和
和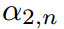 求偏导,得到约束条件。相反,对
求偏导,得到约束条件。相反,对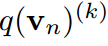 求导得到:
求导得到:
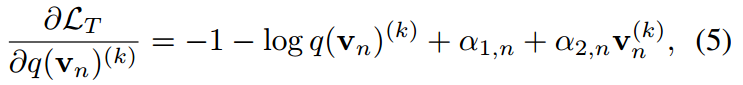
通过使导数为0得到解:
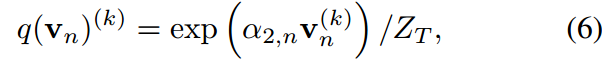
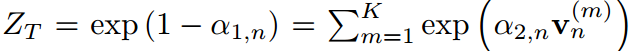 是配分函数满足归一化条件。
是配分函数满足归一化条件。
KD中的softmax推导
根据这一思想,我们定义了一个熵最大化问题来表示KD中的soft最大值。给定一个训练有素的教师及其预测,我们有预测学生的目标函数如下:
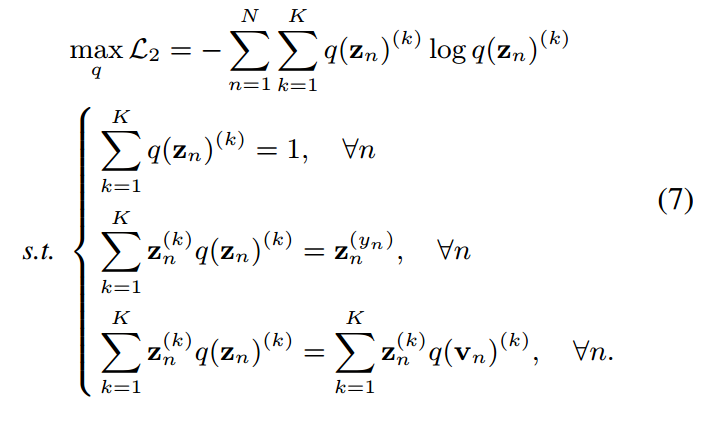
通过应用拉格朗日乘子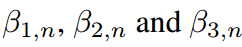
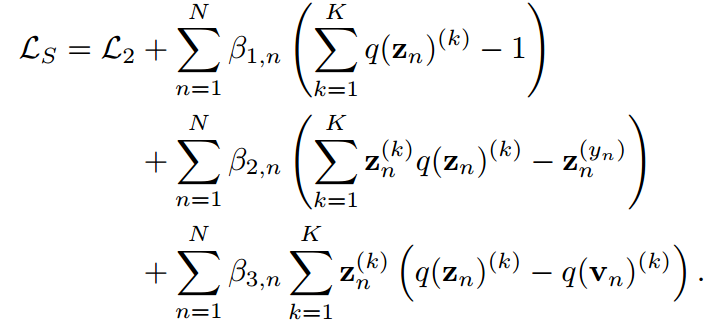
对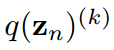 求导得到
求导得到
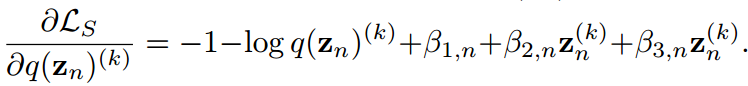
假设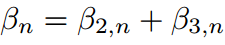 为简单起见,它给出:
为简单起见,它给出:
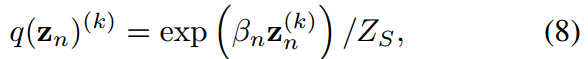
其中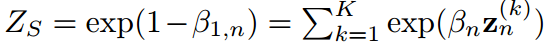 由于概率密度的归一化条件成立。式8中的公式与式6结构相同。
由于概率密度的归一化条件成立。式8中的公式与式6结构相同。
不同的温度
 对
对 的偏导数分别指向Eq.4中的两个约束,并且约束与
的偏导数分别指向Eq.4中的两个约束,并且约束与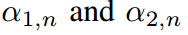 无关。类似的情况也适用于式7.因此,不能给出它们的显示表达式,因此可以手动定义它们的值。如果设
无关。类似的情况也适用于式7.因此,不能给出它们的显示表达式,因此可以手动定义它们的值。如果设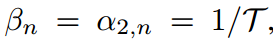 ,则式6和式8转化为涉及学生和教师共同温度的KD表达式。
,则式6和式8转化为涉及学生和教师共同温度的KD表达式。
当时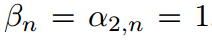 ,公式恢复到分类中常用的传统softmax函数。最终,我们可以选择
,公式恢复到分类中常用的传统softmax函数。最终,我们可以选择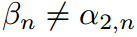 ,这表明教师和学生可以有不同的温度。
,这表明教师和学生可以有不同的温度。
明智的选取不同的温度
通常为所有样本定义一个全局温度。即对于任意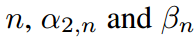 被定义为恒定值。相反,由于缺乏对它们的限制,它们可能在不同的样本中有所不同。选择一个全局常数作为温度缺乏依据。因此,允许采用按样本变化的温度。
被定义为恒定值。相反,由于缺乏对它们的限制,它们可能在不同的样本中有所不同。选择一个全局常数作为温度缺乏依据。因此,允许采用按样本变化的温度。
共用温度的缺点
在本节中,我们展示了传统KD管道中共享温度设置的两个缺点。我们首先通过引入两个超参数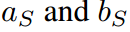 ,将公式8中的softmax用一般公式重写:
,将公式8中的softmax用一般公式重写:
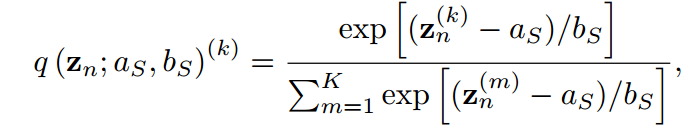
其中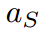 可以消去并且不违反等式。当
可以消去并且不违反等式。当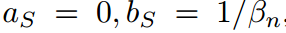 时,会得到公式8中的特殊情况。通过引入
时,会得到公式8中的特殊情况。通过引入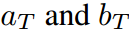 ,可以得到教师情况下的类似方程。
,可以得到教师情况下的类似方程。
对于一个最终得到的很好的蒸馏学生,我们假设KL散度损失达到最小,并且预测教师的密度匹配能力,即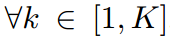 ,
,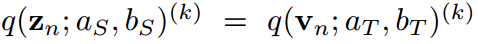 。那么对于任意一对指标
。那么对于任意一对指标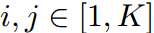 ,很容易得到:
,很容易得到:
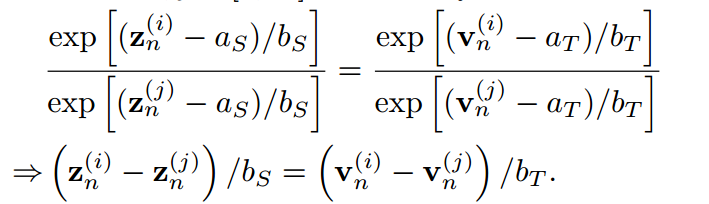
通过对j从1到K求和,我们得到:
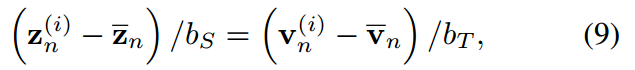
其中,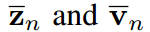 分别为学生和教师logit向量的均值,即
分别为学生和教师logit向量的均值,即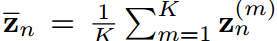 ,(
,(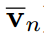 类似)通过等式9对i从1到K的平方求和,我们可以得到:
类似)通过等式9对i从1到K的平方求和,我们可以得到:
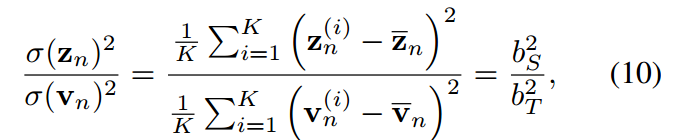
是输入向量标准差的函数。从公式9到10中,我们可以描述一个受过良好训练的学生在loigt移位和方差匹配方面的两个属性。
Logit shift
由式(9)可知,在传统的共享温度( )设置下,学生和教师在任意指标上的对数之间存在恒定的位移,即:
)设置下,学生和教师在任意指标上的对数之间存在恒定的位移,即:
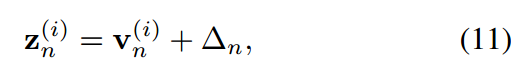
其中,可以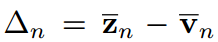 认为是第n个样本的常数。这意味着在传统的KD方法中,学生被迫严格模仿教师转移的logit。考虑到模型大小和容量的差距,学生可能无法像老师那样产生广泛的logit范围。相比之下,当学生的Logit排名与教师匹配时,即给定对教师Logit进行排序的指标
认为是第n个样本的常数。这意味着在传统的KD方法中,学生被迫严格模仿教师转移的logit。考虑到模型大小和容量的差距,学生可能无法像老师那样产生广泛的logit范围。相比之下,当学生的Logit排名与教师匹配时,即给定对教师Logit进行排序的指标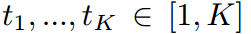 ,使得
,使得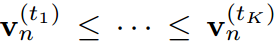 ,则
,则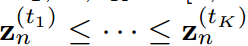 成立。logit关系是使学生和教师一样善于预测基本知识。因此,这种logit变化是基于传统KD管道的副作用,并且会迫使学生产生不必要的困难结果。
成立。logit关系是使学生和教师一样善于预测基本知识。因此,这种logit变化是基于传统KD管道的副作用,并且会迫使学生产生不必要的困难结果。
方差匹配
从公式10中,我们得出结论,学生和教师的温度之比等于他们的预测对数的标准差之比,即:
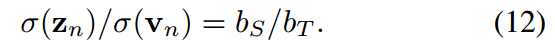
在vanillaKD的温度共享设置中,学生被迫预测logit,使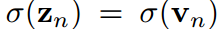 。这是另一个限制学生预测对数标准差的。相反,由于超参数来自拉格朗日乘法器,并且可以灵活调整,我们可以定义
。这是另一个限制学生预测对数标准差的。相反,由于超参数来自拉格朗日乘法器,并且可以灵活调整,我们可以定义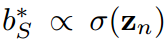 和
和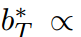
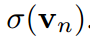 。这样,公式12中的等式总是成立的。
。这样,公式12中的等式总是成立的。
Logits标准化
因此,为了打破这两个束缚,我们建议将超参数分别设置为其对数的均值和加权标准差,即:
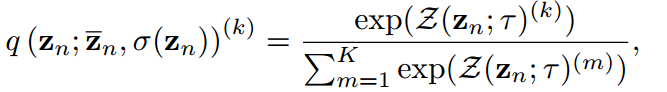
其中,Z为算法中的Z-score函数。教师logit的情况与此类似,略去。在教师模型和学生模型中引入并共享一个基础温度T。Z-score标准化至少有4个有利的性质,即0均值、有限标准差、单调性和有界性。
0均值
标准化向量的均值很容易被证明为0.在以前的工作中,假设平均值为0,并且通常在经验上违反。相反,Z-score函数本质上保证平均值为0。
有限标准差
加权Z-score输出的标准差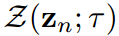 可以表示为1/T。这个性质使标准化的学生和教师logit对数映射到一个相同的高斯分布,平均值为0,标准差确定。表转化的映射是多对一的,这意味着它的反向是不确定的。因此,原始学生logit向量
可以表示为1/T。这个性质使标准化的学生和教师logit对数映射到一个相同的高斯分布,平均值为0,标准差确定。表转化的映射是多对一的,这意味着它的反向是不确定的。因此,原始学生logit向量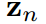 的方差和取值范围不受限制。
的方差和取值范围不受限制。
单调性
很容易证明Z-score是一个线性变换函数,因此这是单调函数。这种属性确保转换后的学生logit与原始logit保持相同的排名。因此,教师logit中必要的内在关系得以保留并转移给学生。
有界性
标准化的对数可以在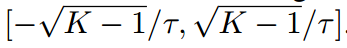 范围内表示。与传统KD相比,可以控制logit范围,避免指数值过大。为此,我们定义了一个基本温度来控制范围。
范围内表示。与传统KD相比,可以控制logit范围,避免指数值过大。为此,我们定义了一个基本温度来控制范围。
所提出的logit标准化预处理伪代码在算法2中给出。
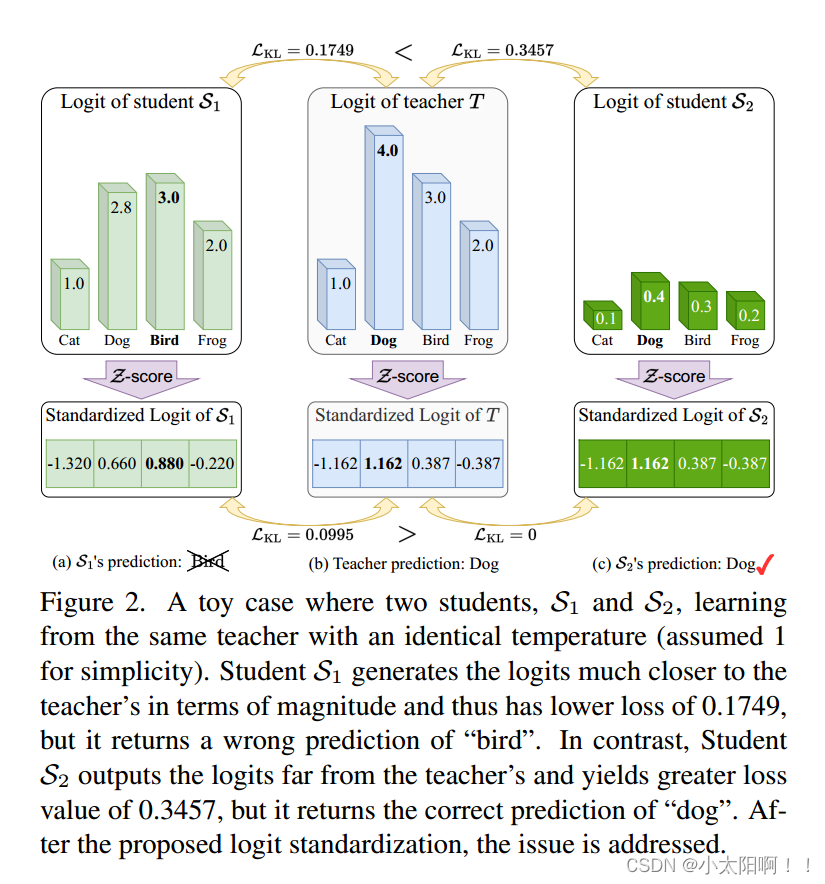
Toy Case
图2展示了一个典型的案例,其中传统的基于logit的共享温度KD设置可能会导致对学生成绩的不真实评估。第一个学生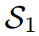 预测的对数在量级上更接近教师T,而第二个学生
预测的对数在量级上更接近教师T,而第二个学生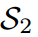 保留了与老师相同的固有对数关系。因此,的KL散度损失较低,为0.1749,明显优于第二位学生
保留了与老师相同的固有对数关系。因此,的KL散度损失较低,为0.1749,明显优于第二位学生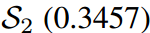 。然而,
。然而,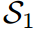 对“Bird”的预测是错误的,而
对“Bird”的预测是错误的,而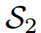 对”dog“的预测是正确的,这与损失对比是矛盾的。通过应用我们的Z分数,所有logit都被重新缩放,并且在评估中强调logit之间的关系而不是它们的大小。即
对”dog“的预测是正确的,这与损失对比是矛盾的。通过应用我们的Z分数,所有logit都被重新缩放,并且在评估中强调logit之间的关系而不是它们的大小。即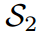 的损失为0,远好于
的损失为0,远好于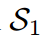 的0.0995,这与预测到的预测是一致的。
的0.0995,这与预测到的预测是一致的。
这篇关于Logit Standardization in Knowledge Distillation 知识蒸馏中的logit标准化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









