改进猫群算法丨多车场多车型路径问题求解复现

本文主要是介绍改进猫群算法丨多车场多车型路径问题求解复现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

车间调度系列文章：

• 1、路径优化历史文章
• 2、路径优化丨带时间窗和载重约束的CVRPTW问题-改进遗传算法：算例RC108
• 3、路径优化丨带时间窗和载重约束的CVRPTW问题-改进和声搜索算法：算例RC108
• 4、路径优化丨复现论文-网约拼车出行的乘客车辆匹配及路径优化
• 5、多车场路径优化丨遗传算法求解MDCVRP问题
• 6、论文复现详解丨多车场路径优化问题:粒子群+模拟退火算法求解
• 7、路径优化丨复现论文外卖路径优化GA求解VRPTW
• 8、多车场路径优化丨蚁群算法求解MDCVRP问题
• 9、路径优化丨复现论文多车场带货物权重车辆路径问题：改进邻域搜索算法
• 10、多车场多车型路径问题求解复现丨改进猫群算法求解

问题描述

多车场多车型车辆路径问题可描述为：多个车场内配备多种类型的车辆，服务周边的客户，已知所有客户的需求，同时，已知客户的位置坐标，通过合理地分配车辆和客户，制定合理的配送方案，使得配送成本最低。示意图如下：

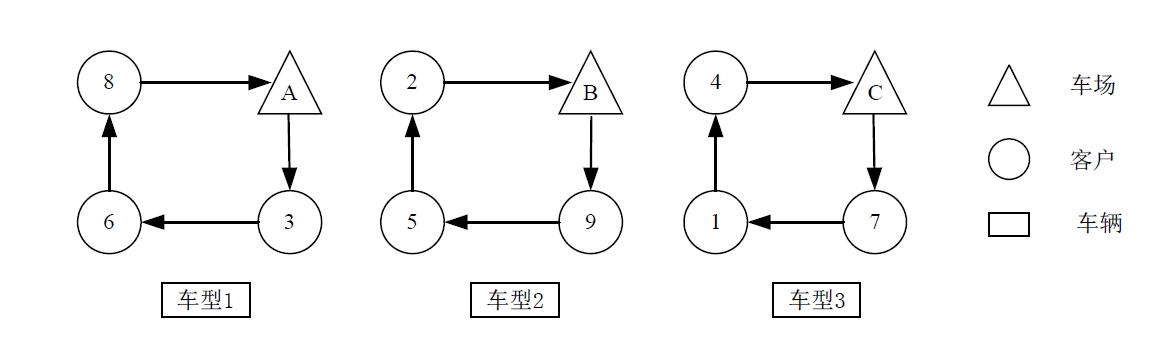
为了方便对问题进行分析和求解，首先设置了如下假设：

• （1）车辆完成任务后，停靠原车场；
• （2）每个车场拥有不同类型的车辆，不同类型车辆的载重、使用成本等属性可能不同；
• （3）一辆车最多被使用一次；
• （4）已知客户相关信息，各个车场和车辆的相关信息已知；
• （5）每辆车至少可以服务一个客户，即每辆车的额定载重不小于任意一个客户的需求；
• （6）每个客户只能被一辆车服务，且只访问一次。

数学模型

具体模型见参考文献。模型相关的参数和变量如下：

𝑀：客户的数量；

𝐾：车辆的数量；

𝑁：车场的数量；

𝐿 ：车型的数量；

𝑦𝑛：车场𝑛(𝑛 = 1,2,3 … , 𝑁)内的车辆数目；

𝑅𝑛𝑙：车场𝑛(𝑛 = 1,2,3 … , 𝑁)的第𝑙 (𝑙 = 1,2,3 … , 𝐿)种类型的车辆数目；

𝐼𝑘：车辆 𝑘 服务客户的编号集合；

𝑓𝑘1：车辆𝑘 的固定成本；

𝑓𝑘2：车辆𝑘 的可变成本；

𝑄1𝑘：车辆𝑘 的额定载重；

𝑄2𝑙：车型𝑙 的额定载重；

𝑑𝑖𝑗：节点𝑖 到节点𝑗 的距离；

𝑞𝑖：节点𝑖 的需求量；

简单说目标函数是目标函数是不变成本和可变成本之和。不变成本是每辆车的固定成本，可变成本是每辆车的运行成本，和经过的客户点有关系。

数据预处理

论文数据，
30个客户：

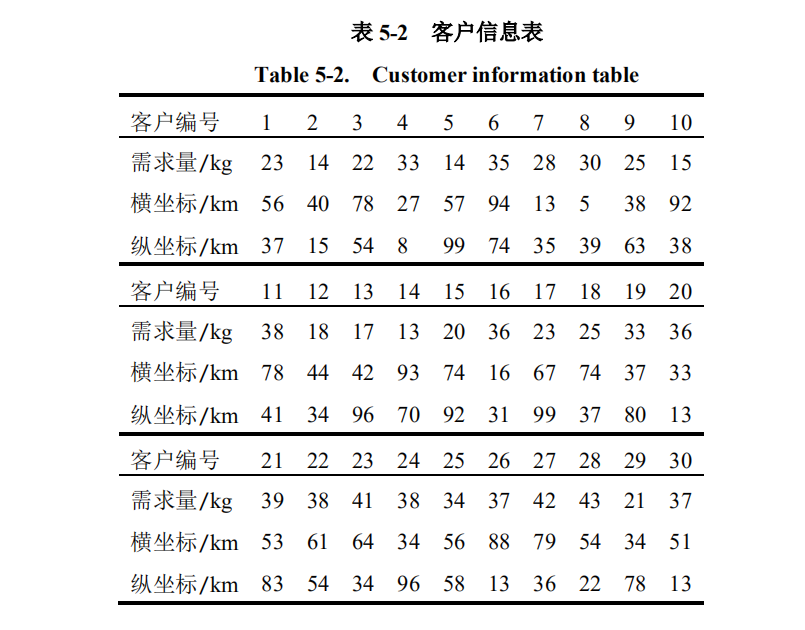
10个车辆：

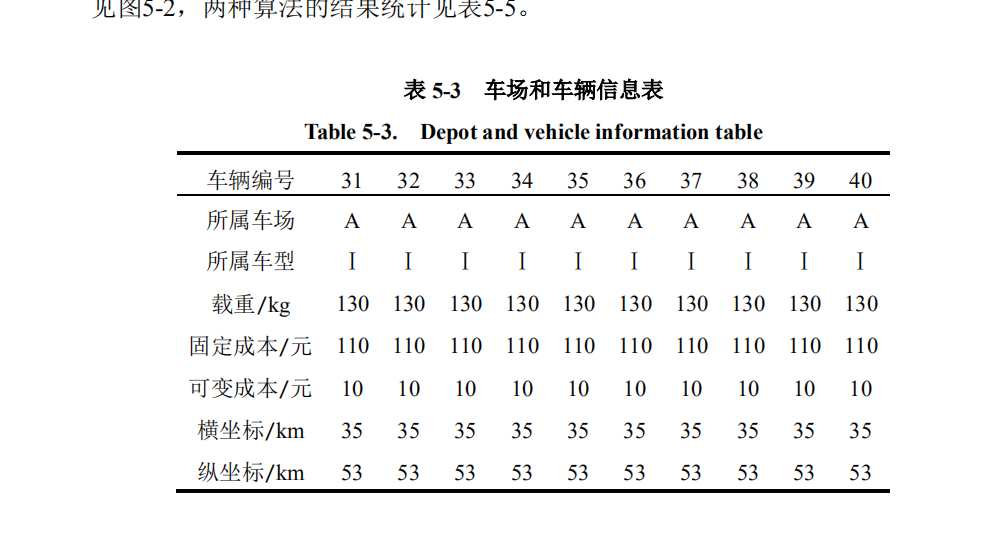
复制数据到对应txt：

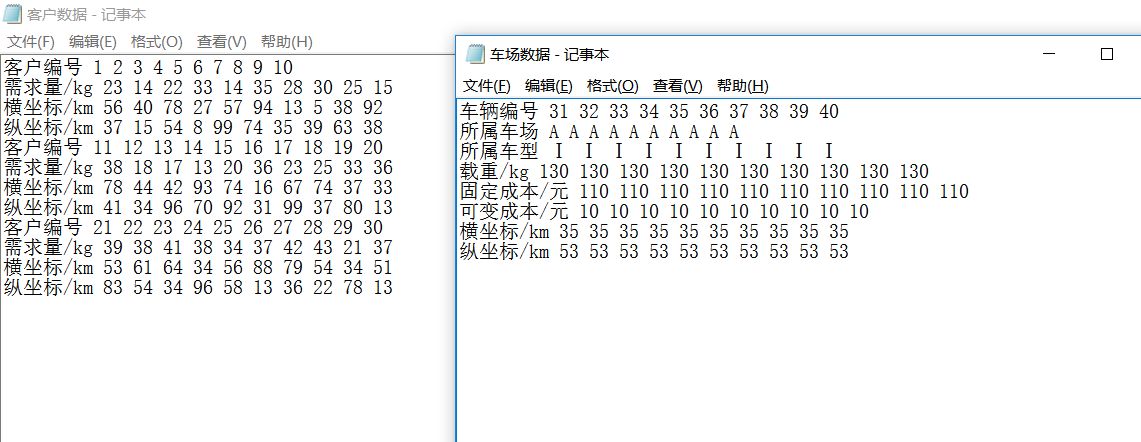
正则读取对应行就行。

import redef get_customer():with open('客户数据.txt', 'r') as file:content = file.read()  # 读取文件内容demand_inf = re.findall(r'需求量/kg[0-9 ]+', content)xust_inf = re.findall(r'横坐标/km[0-9 ]+', content)yust_inf = re.findall(r'纵坐标/km[0-9 ]+', content)demand, x, y = [], [], []for dxy in range(len(demand_inf)):demand += [int(d) for d in re.findall(r'[0-9]+', demand_inf[dxy])]x += [int(xx) for xx in re.findall(r'[0-9]+', xust_inf[dxy])]y += [int(yy) for yy in re.findall(r'[0-9]+', yust_inf[dxy])]return demand, x, ydef get_park():with open('车场数据.txt', 'r') as file:content = file.read()  # 读取文件内容load_inf = re.findall(r'载重/kg[0-9 ]+', content)unchange_inf = re.findall(r'固定成本/元[0-9 ]+', content)change_inf = re.findall(r'可变成本/元[0-9 ]+', content)xust_inf = re.findall(r'横坐标/km[0-9 ]+', content)yust_inf = re.findall(r'纵坐标/km[0-9 ]+', content)load_all = [int(l) for l in re.findall(r'[0-9]+', load_inf[0])]unchange_c = [int(u) for u in re.findall(r'[0-9]+', unchange_inf[0])]change_c = [int(c) for c in re.findall(r'[0-9]+', change_inf[0])]x_center = [int(xx) for xx in re.findall(r'[0-9]+', xust_inf[0])]y_center = [int(yy) for yy in re.findall(r'[0-9]+', yust_inf[0])]return load_all, unchange_c, change_c, x_center, y_center

运行环境

windows系统，python3.6.0,第三方库及版本号如下：

numpy==1.18.5
matplotlib==3.2.1

第三方库需要在安装完python之后，额外安装，以前文章有讲述过安装第三方库的解决办法。

算法设计

1、编码

编码介绍

论文采用实数编码，一段表示车辆，一段表示客户：

本文做了改进：把编码拆开成2段，分别是车辆和客户，为了下面的猫群算子操作更容易。

编码生成

车辆编码生成： 随机打乱车辆编号

客户编码生成：随机选择一辆车的车场作为原点，扫码周围客户点，按距离形成序列，按载重依次分配给车辆。

代码：

def init_road(self):road_car = [[] for i in range(len(self.load_all))]car_idx = np.arange(len(self.load_all))random.shuffle(car_idx)                # 随机打乱车辆编号idx = random.choice(car_idx)           # 选择一个作为原点origin_x, origin_y = self.x_center[idx], self.y_center[idx]dist = [np.sqrt((self.x[point] - origin_x)**2 + (self.y[point] - origin_y)**2) for point in range(len(self.demand))]dist_sort = np.array(dist).argsort()   # 计算与周围客户点距离后，按大小索引形成序列road = dist_sort.tolist()car_count = 0for cust_idx in dist_sort:             # 遍历序列的每一个点idx1 = car_idx[car_count]if sum(np.array(self.demand)[road_car[idx1]]) + self.demand[cust_idx] > self.load_all[idx1]:car_count += 1                # 载重不满足时换下一辆车idx1 = car_idx[car_count]road_car[idx1].append(cust_idx)return car_idx.tolist(), road_car, road

文献数据形成的可行编码如下:

车辆编码：[4, 9, 3, 7, 2, 0, 1, 6, 5, 8]

表示优先安排车辆5(4+1)，车辆10配送，后面以此类推

客户编码：[8, 11, 24, 28, 21, 0, 18, 6, 15, 7, 22, 20, 27, 1, 19, 17, 2, 23, 29, 12, 10, 3, 26, 4, 14, 16, 9, 13, 5, 25]

表示优先服务客户9(8+1)，客户12，后面以此类推

车辆客户编码：[[29, 12, 10, 3], [26, 4, 14, 16, 9, 13], [19, 17, 2, 23], [15, 7, 22], [8, 11, 24, 28], [], [5, 25], [20, 27, 1], [], [21, 0, 18, 6]]

因为优先安排车辆5且考虑载重，所以8,11,24,28被分到第5个括号，然后21,0,18,6被分到最后一个括号，后面以此类推。其中，车辆6和车辆9没有分到，为空括号。

2、解码

一个车辆的解码如下：

• 1、 根据车辆和客户编码读出各点的坐标和需求；

• 2、 编码客户的第一个点时，计算车场到点的距离，其余点计算与上一个客户点的距离，更新可变成本；

• 3、每辆车遍历到最后一个点时，计算点到车场的距离，成本更新（包含不变成本），解码结束：

代码如下：

    def decode(self, car_idx, road_car):fk1, fk2 = 1, 1C1 = 0C2 = [0 for i in range(len(self.load_all))]count = 0for rc in road_car:fk1 = self.unchange_c[count]        # 单位固定成本fk2 = self.change_c[count]          # 单位可变成本if rc:                              # 车辆的客户点非空C1 += fk1                       # 固定成本计算idx = car_idx[count]for point in rc:if C2[count] == 0:          # 车场到第一个客户origin_x, origin_y = self.x_center[idx], self.y_center[idx]dist = np.sqrt((self.x[point] - origin_x)**2 + (self.y[point] - origin_y)**2) C2[count] += dist*fk2   # 可变成本计算​    else :                       # 客户点之间运行dist = np.sqrt((self.x[point] - x_start)**2 + (self.y[point] - y_start)**2) C2[count] += dist*fk2     # 可变成本计算x_start, y_start = self.x[point], self.y[point] # 车辆再回车场dist = np.sqrt((origin_x - x_start)**2 + (origin_y - y_start)**2) C2[count] += dist*fk2           # 可变成本计算count += 1return C1, C2, C1 + sum(C2)

猫群算子

逆序邻域搜索算子

车辆或者客户截取一段编码逆序即可：

def Reverse_order(road, signal):loc = random.sample(range(len(road)), 2)             # 选取2个位置loc.sort()                                           # 保证位置从小到大road1, road2, road3 = road[:loc[0]], road[loc[0]:loc[1]], road[loc[1]:] # 截取编码road2.reverse()                                      # 逆序return road1 + road2 + road3                         # 返回合并的新代码

1—opt算子

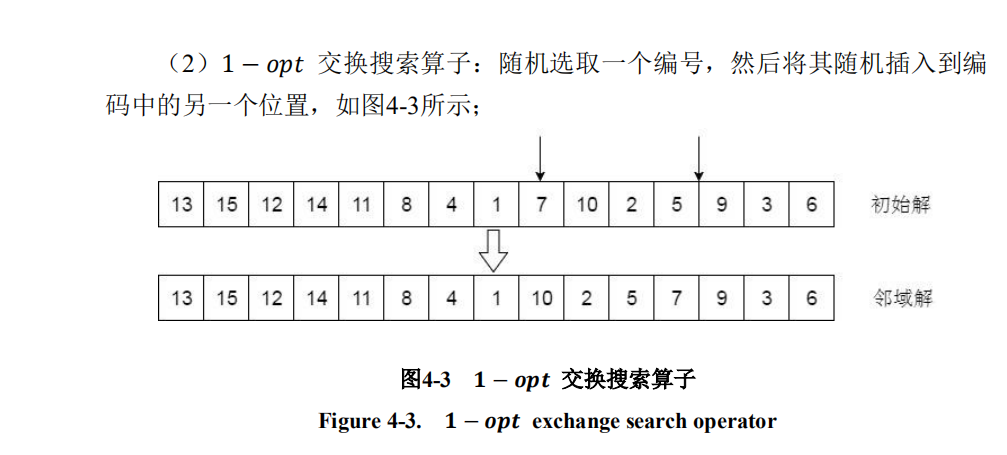
代码：

    def opt_1(road, signal):loc = random.sample(range(len(road)), 2)             # 选取2个位置if signal==1:while max(loc) < len(road)/2:                    # 保证车辆编码的一个位置在后半边编码，文献有说到loc = random.sample(range(len(road)), 2)loc.sort()                                           # 位置升序a = road[loc[0]]b_idx = loc[1]road.remove(a)                                       # 找到编码，移除road.insert(b_idx-1, a)                              # 插入编码，-1是因为上一步移除，位置缩进return road

2-opt算子

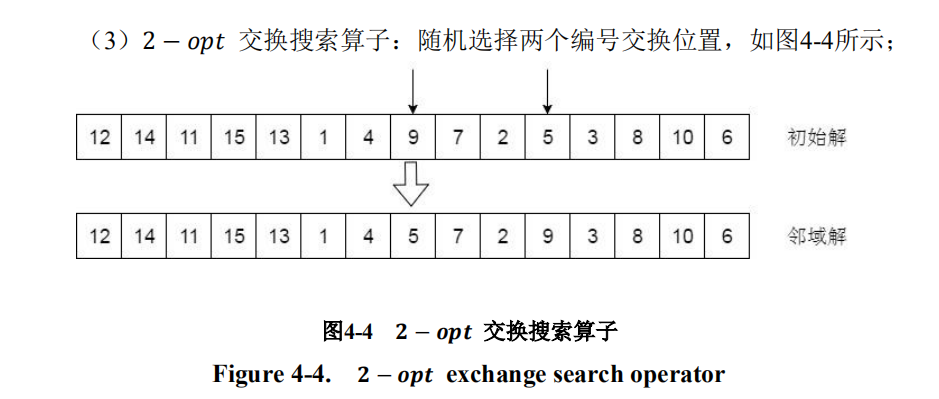
代码：

def opt_2(road, signal):loc = random.sample(range(len(road)), 2)            if signal==1:while max(loc) < len(road)/2:                    # 保证车辆编码的一个位置在后半边编码，文献有说到loc = random.sample(range(len(road)), 2)road[loc[0]], road[loc[1]] = road[loc[1]], road[loc[0]]  # 2个位置交换return road

3—opt算子

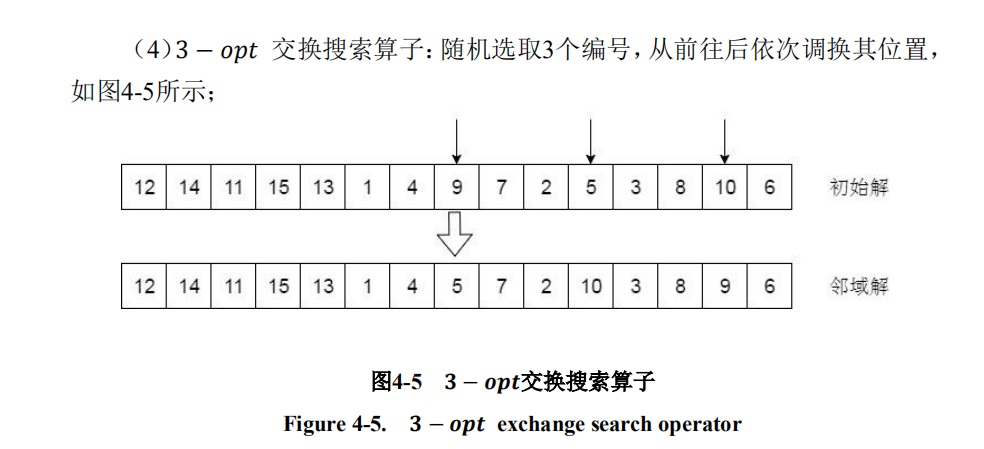
相当于上面的2_opt交换2次

代码：

def opt_3(road, signal):loc = random.sample(range(len(road)), 3)if signal==1:while max(loc) < len(road)/2:                   # 保证车辆编码的一个位置在后半边编码，文献有说到loc = random.sample(range(len(road)), 3)road[loc[0]], road[loc[1]] = road[loc[1]], road[loc[0]] # 交换1次road[loc[1]], road[loc[2]] = road[loc[2]], road[loc[1]] # 交换2次return road

2、跟踪最优算子

简单来说：2段编码截取长度为U的一段，找出相同的基因，编码2去掉这段基因，剩余的基因左连接去掉的这段基因。详细介绍见文献

def follow_best(road1, road2, U):road2 = road2.tolist()a_u = road1[:U]              # 截取1段b_u = road2[:U]              # 截取1段road3 = []for a in a_u:       if a in b_u:            # 截取片段有相同基因时road3.append(a)     # 保存基因road2.remove(a)     # 编码2移除基因road3 += road2              # 最后左连接return road3

3、跟踪中心算子

重要的是找出中心编码，找到中心编码后的该编码看作最优编码，跟踪方式相同。中心编码寻找如下：

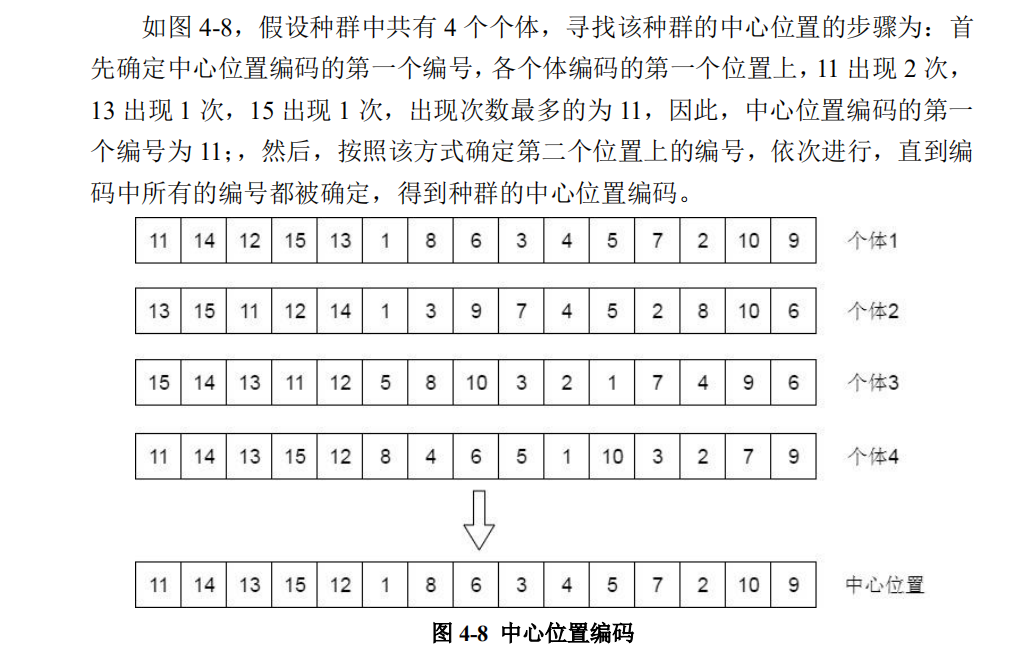
简单来说，统计所有位置出现最多的基因，保证客户基因不重复的情况，出现次数最多基因连起来的就是中心编码

代码：

def center_road(T_road):cent_road = []T_road = T_road.tolist()                 # 备份一份while T_road[0]:                         # 当还存在编码非空时road_time = [ro[0] for ro in T_road] # 各个编码的第一个基因b = Counter(road_time)               # 计数ansdict = b.most_common(1)           # 出现次数最多的情况rox = ansdict[0][0]cent_road.append(rox)                # 出现最多的基因for i in range(len(T_road)):         # 中心编码找到一个基因后，所有编码依次移除该基因T_road[i].remove(rox)return cent_road

改进猫群算法设计

改进猫群算法的具体步骤如下：

• （1）初始化参数和路径信息，并且生成初始的种群；

• （2）根据设置的分组率，选出实施搜寻行为的个体，剩余的个体则全部实施跟踪行为；

• （3）个体根据各自的行为，分别更新位置，即跟踪模式下的个体执行跟踪模式，其余则执行搜寻模式；

• （4）更新种群中个体的适应度，同时记录最优个体；

• （5）判断迭代次数，若代数符合算法的设置，则对当前最优解进行一次模拟退火搜索；否则，则跳过该步骤，转步骤（6）；

• （6）检查结束条件。若符合算法终止条件，则得到优化结果；否则，继续执行（2）

推文没设置分组率，全部都进行搜寻和跟踪，有兴趣自行设置，修改比较容易，文献是最后一次迭代对最优个体进行一次模拟退火，

1、搜寻模式

（1）将 𝐿𝑠 复制 𝑉 份，并存入记忆池；

（2）对每个副本实施搜索，首先确定对位置编码的车辆编码部分或客户编码部分进行搜索。若𝑣(𝑣 = 1,2,3, … … , 𝑉)能够被 4 整除（即每 4 个中有一个对车辆编码搜索），则对车辆编码部分进行搜索；否则，对客户编码部分进行搜索。搜索完成之后，获得新的候选位置 𝐿𝑠𝑣 (𝑣 = 1,2,3, … … , 𝑉)；

（3）解码计算每个候选位置 𝐿𝑠𝑣 的适应度 𝑓𝑠𝑣 ，记录其中最优的适应度为 𝑓b ，最优位置为 𝐿b ；

（4）若 𝑓𝑠 ≥ 𝑓b ,则保持𝐿𝑠 不变；否则，用𝐿b 代替 𝐿𝑠 。

简单来说：个体在执行搜寻模式时，使用选择算子从记忆池中选择适应度最高（成本最低）的位置作为该个体的新位置。

代码：

def search(self, car_idx, road):                            # 搜索模式road_car = self.cd.road_code(car_idx, road)             # 客户路径转换C1, C2, fs = self.cd.decode(car_idx, road_car)          # 初始的成本T_road = np.zeros((self.𝑉, len(road)), dtype = np.int)                  # 客户池T_caridx = np.zeros((self.𝑉, len(car_idx)), dtype = np.int)             # 车辆池T_road[:] = roadT_caridx[:] = car_idx for v_idx in range(self.𝑉):Operator = ['Reverse_order', 'opt_1', 'opt_2', 'opt_3']oper = random.choice(Operator)                      # 随机选择一个算子car_code = T_caridx[v_idx].tolist()ro_code = T_road[v_idx].tolist()if v_idx%4 == 0:                                    # 如果被4整除，车辆搜索          car_code = eval(f'cat.{oper}(car_code, 1)')else:                                               # 否则，客户搜索ro_code = eval(f'cat.{oper}(ro_code, 0)')road_car = self.cd.road_code(car_code, ro_code)     # 路径转换C1, C2, fb = self.cd.decode(car_code, road_car)     # 新路径的成本if fb < fs:                                         # 如果成本优于初始成本，更新编码和成本car_idx = car_coderoad = ro_codefs = fbreturn car_idx, road, fs

2、跟踪模式

改进猫群算法的跟踪模式有两种情况：

• 1、跟踪种群中的最优个体的位置，
• 2、跟踪种群的中心位置。

需要说明的是，执行跟踪模式的猫，每次只能选择执行跟踪其中的一个位置，即每次随机选择跟踪最优个体或中心位置。

每次跟踪在一定概率下跟踪最优个体，否则跟踪中心个体，相关算子上面有介绍。

代码：

def follow(self, T_car, T_road):                           # 跟踪模式f_all = [self.cd.decode(T_car[i],self.cd.road_code(T_car[i],T_road[i]))[-1] for i in range(len(T_car))]best_idx = f_all.index(min(f_all))           f_best = min(f_all)                                    best_car, best_road = T_car[best_idx].tolist().copy(), T_road[best_idx].tolist().copy()# 最优个体center_road = cat.center_road(T_road)                  # 中心个体center_car = cat.center_road(T_car)for i in range(len(f_all)):car = T_car[i]road = T_road[i]if random.random() < self.𝜃 and i != best_idx:     # 一定概率下跟踪最优个体road_new = cat.follow_best(best_road, road, self.𝑈)road_car = self.cd.road_code(car, road_new)C1, C2, fb = self.cd.decode(car, road_car)if fb < f_best:                                # 如果新个体优于最优个体best_car = carbest_road = road_new                       # 更新最优客户路径f_best = fbelse:                                              # 否则跟踪中心个体road_new = cat.follow_best(center_road, road, self.𝑈)road_car = self.cd.road_code(car, road_new)C1, C2, fb = self.cd.decode(car, road_car)if fb < f_best:best_car = carbest_road = road_newf_best = fbT_road[i] = road_new                              # 更新种群客户road_car = self.cd.road_code(best_car, best_road)C1, C2, fs = self.cd.decode(best_car, road_car) return T_road, best_car, best_road, f_best

3、模拟退火算法

概念不再赘述,文献的算法步骤是：

（1）在前𝐻/2 次，对编码的客户编码部分实施变异，车辆编码部分不变，具体操作为：随机选择其中的一个算子，对客户编码部分执行搜索，产生新的位置，如果min(1, exp[−(𝑍(𝐿𝑏) − 𝑍(𝐿𝑎)) / 𝐸tem-])+ ≥ random(0,1)，则令𝐿𝑎 = 𝐿𝑏；记录该过程的最优位置𝐹sa及其适应度𝑓sa；

（2）在后𝐻/2 次，对编码的车辆编码部分实施变异，客户编码部分不变，具体操作为；随机选择其中的一个算子，对车辆编码部分执行搜索，产生新的位置，如果min(1, exp[−(𝑍(𝐿𝑏) − 𝑍(𝐿𝑎)) / 𝐸tem-])+ ≥ random(0,1)，则令𝐿𝑎 = 𝐿𝑏；记录该过程的最优位置𝐹sa及其适应度𝑓sa；

（3）令 𝐸tem = 𝐸tem ∗ 𝑟 ，若 𝐸tem ≤ 𝐸2，则终止搜索，进行判断：若𝑓sa > 𝑓best，则令𝐿best = 𝐿sa，𝑓best = 𝑓sa，否则，令𝐹best不变，避免出现退化；若 𝐸tem > 𝐸2，则重新回到步骤（1）。

简单来说，一定概率下接受新个体，且一直保留或更新最优个体。文献是再最后一次迭代后对最优个体进行模拟退火。

def Simul(self, best_car, best_road, f_best):if type(best_car) == np.ndarray:carx = best_car.tolist().copy()else:carx = best_car.copy()if type(best_road) == np.ndarray:roadx = best_road.tolist().copy()else:roadx = best_road.copy()fbx = f_bestroad_car = self.cd.road_code(best_car, best_road)C1, C2, fs = self.cd.decode(best_car, road_car) while self.𝐸1 > self.𝐸2:for i in range(self.𝐻):Operator = ['Reverse_order', 'opt_1', 'opt_2', 'opt_3']oper = random.choice(Operator)if i < self.𝐻/2:road1 = eval(f'cat.{oper}(roadx, 0)')      # 产生新客户路径road_car = self.cd.road_code(carx, road1)C1, C2, fb = self.cd.decode(carx, road_car)if min(1, np.exp(-(fb-fbx)/self.𝐸1)) >= random.random():  # 一定概率接受新路径roadx = road1fbx = fbif fb < f_best: best_car = carx                  best_road = road1f_best = fbelse:car1 = eval(f'cat.{oper}(carx, 1)')        # 产生新车辆路径road_car = self.cd.road_code(car1, roadx)C1, C2, fb = self.cd.decode(car1, road_car)if min(1, np.exp(-(fb-fbx)/self.𝐸1)) >= random.random():carx = car1fbx = fbif fb < f_best:                             # 成本得到优化就更新print('2222')best_car = car1best_road = roadxf_best = fbself.𝐸1 *= self.𝑟                                   # 温度更新return best_car, best_road, f_best

结果

设计主函数如下：

import data
from code_decode import co_de
import numpy as np
import paint
from cat_change import cat_chdemand, x, y = data.get_customer()   # 客户数据
load_all, unchange_c, change_c, x_center, y_center = data.get_park() # 车辆数据
parm_data = [demand, x, y, load_all, unchange_c, change_c, x_center, y_center]
cd = co_de(parm_data)                            # 解码模块
car_init, road_car, road_init = cd.init_road()  
C1, C2, fs = cd.decode(car_init, road_car)       # 初始成本𝑆 = 20             # 猫的种群数量
δ = 0.1             # 分组率
𝑉 = 40              # 记忆池容量
𝑇 = 10            # 迭代总次数
𝑈 = 18              # 比对长度
𝜃 = 1             # 跟踪最优个体概率
𝜃1 = 0.2            # 跟踪中心位置概率1 − 𝜃
𝐸1 = 100            # 初始温度
𝐸2 = 95              # 终止温度
𝑟 = 0.99            # 降温系数
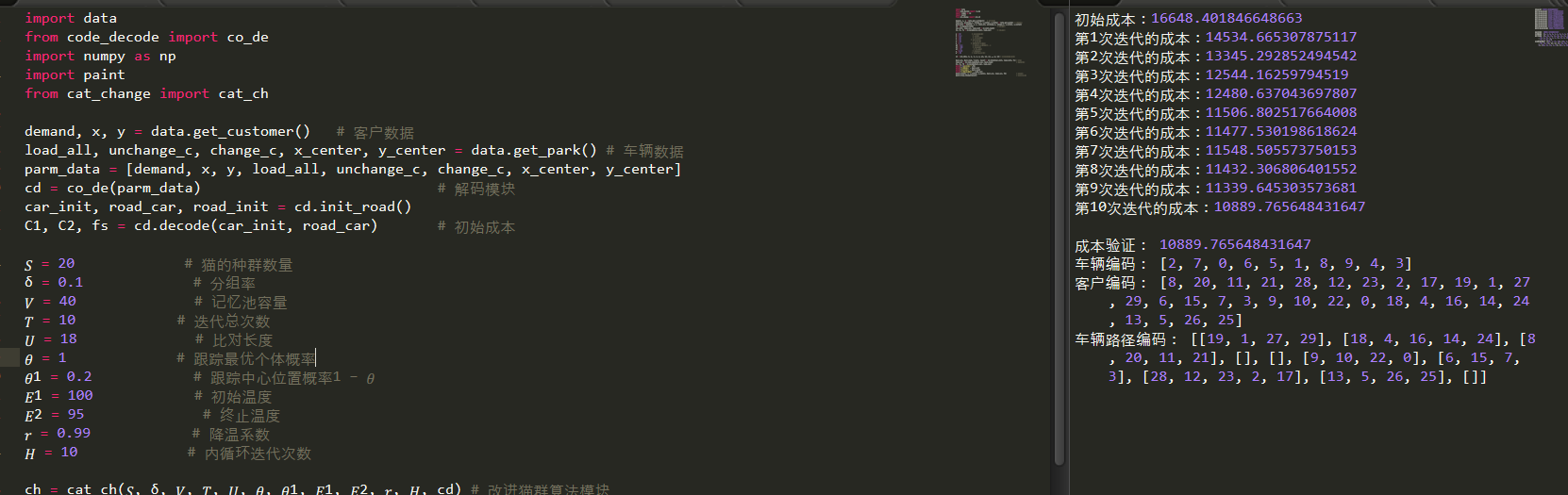
𝐻 = 10             # 内循环迭代次数ch = cat_ch(𝑆, δ, 𝑉, 𝑇, 𝑈, 𝜃, 𝜃1, 𝐸1, 𝐸2, 𝑟, 𝐻, cd) # 改进猫群算法模块best_car, best_road, f_best, result = ch.total(car_init, road_init, fs) # 结果
road_car = cd.road_code(best_car, best_road)                            # 编码转换
C1, C2, fb = cd.decode(best_car, road_car) 
print("\n成本验证：",fb) 
print('车辆编码：', best_car)
print('客户编码：', best_road)
print('车辆路径编码：', road_car)
paint.draw(x, y, x_center, y_center, best_car, road_car, fb)            # 路径图
paint.draw_change(result)                                               # 成本变化图

运行结果

结果如下：

路径图：

成本随迭代次数的变化图如下：

还有优化空间，增大种群规模和迭代次数试试。

小结

• 本文主要是对参考论文进行复现，有小改动，但基本是复现原文，具体算法步骤见文献，不做过多介绍。本推文只是复现文献的部分内容，严格来说是单车场路径规划问题，应该文献的多车场数据也能运行，但还没做测试，不能运行修改也不会很大。至于带时间窗的模型，可能后续会复现。

• 本文数据和算法皆可修改（考虑运行时间，推文把一些运行参数调低）。

• 参考文献：
  [1]蒋权威.多车场多车型车辆路径问题的改进猫群算法[D].浙江工业大学,2020.DOI:10.27463/d.cnki.gzgyu.2020.001279.

代码

为了方便和便于修改和测试，把代码在6个代码里。有兴趣可以任意合并，减少文件数。

演示视频：

完整算法+数据：
完整算法源码+数据：见下方微信公众号：关注后回复：调度

# 微信公众号：学长带你飞
# 主要更新方向：1、柔性车间调度问题求解算法
#              2、学术写作技巧
#              3、读书感悟
# @Author  : Jack Hao

这篇关于改进猫群算法丨多车场多车型路径问题求解复现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---