本文主要是介绍江苏气象AI算法挑战赛亚军比赛攻略_DontMind队,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
关联比赛: 2022江苏气象AI算法挑战赛-AI助力强对流天气预报
江苏气象AI算法挑战赛亚军比赛攻略_DontMind队
成员介绍

一、赛题分析
本次比赛主要是针对大风/雷达回波/降水的短临预报,属于典型的时空序列预测问题,此类问题可以从分类和回归预测两个角度来解决。
- 按照各气象要素阈值区间进行分类,可以转化为分类预测问题;
- 从回归预测的角度又分为单变量回归预测和多变量回归预测。
由于大风和降水预测很难转换为分类预测问题,而且我们经过大量的模型试验表明,多变量回归预测很难同时达到最优,且很难超越单变量回归预测。
因此,我们最终采用了单变量回归预测思路,并利用过去一小时数据预测未来两小时各气象要素的时空演变。以下将围绕我们决赛最终采用的模型和策略进行介绍

二、总体设计思路

三、数据预处理
数据清洗: 去除雷达回波低值伪影以及异常降水值。
样本重采样和降采样: 由于数据分布不平衡问题,根据各要素阈值区间分布情况对样本进行重采样和降采样,以平衡不同强度样本占比。
数据集调整: 由于所给的数据集中相邻个例仅相差一帧,重复率过高,因此我们将临近个例的间隔调整为5帧,降低样本重叠率,提升模型训练稳定性。

四、模型选择与优化
风速预测—— SEResNet

雷达回波预测模型——TrajGRU

降水预测模型:双模型融合
模型一:U2Net

模型二:PhyDNet

双模型融合:两个模型预测结果取平均
五、损失函数

针对不同模型,设计不同损失函数,由于本赛题预测对象均有严重不平衡问题,因此针对MSE和MAE类型损失函数需要给与相应权重设置。而DiceLoss本身仅针对目标区域计算损失,因此无需再给定权重。
此外,针对降水,加入了60/90/120min的累计降水的损失作为正则项。
六、性能提升策略
- Two-stage优化: 冻结模型部分层,调整损失函数权重,调低学习率,进行模型参数微调,提高强回波/降水的预测技能评分
- 模型集成: 针对降水预测,融合U2Net与PhyDNet预测,提升模型泛化能力和稳定性
- 偏差订正: 考虑了预测能力的时间衰减和阈值的影响,对模型预测进行偏差订正,提高强回波/降水的预测技能评分

七、官方个例真实性
风速预测


雷达回波


降水预测




八、总结
- 样本不平衡: 样本重采样+损失加权和正则/类别不平衡损失+Two-stage优化减轻类别极度不平衡导致的强回波/降水难预测问题
- 模型性能及稳定性: 多模型集成进一步提高降水的整体预报技能评分及模型的稳定性
- 后处理方法: 引入模型预测偏差订正后处理方法提高强回波/降水预报技能评分
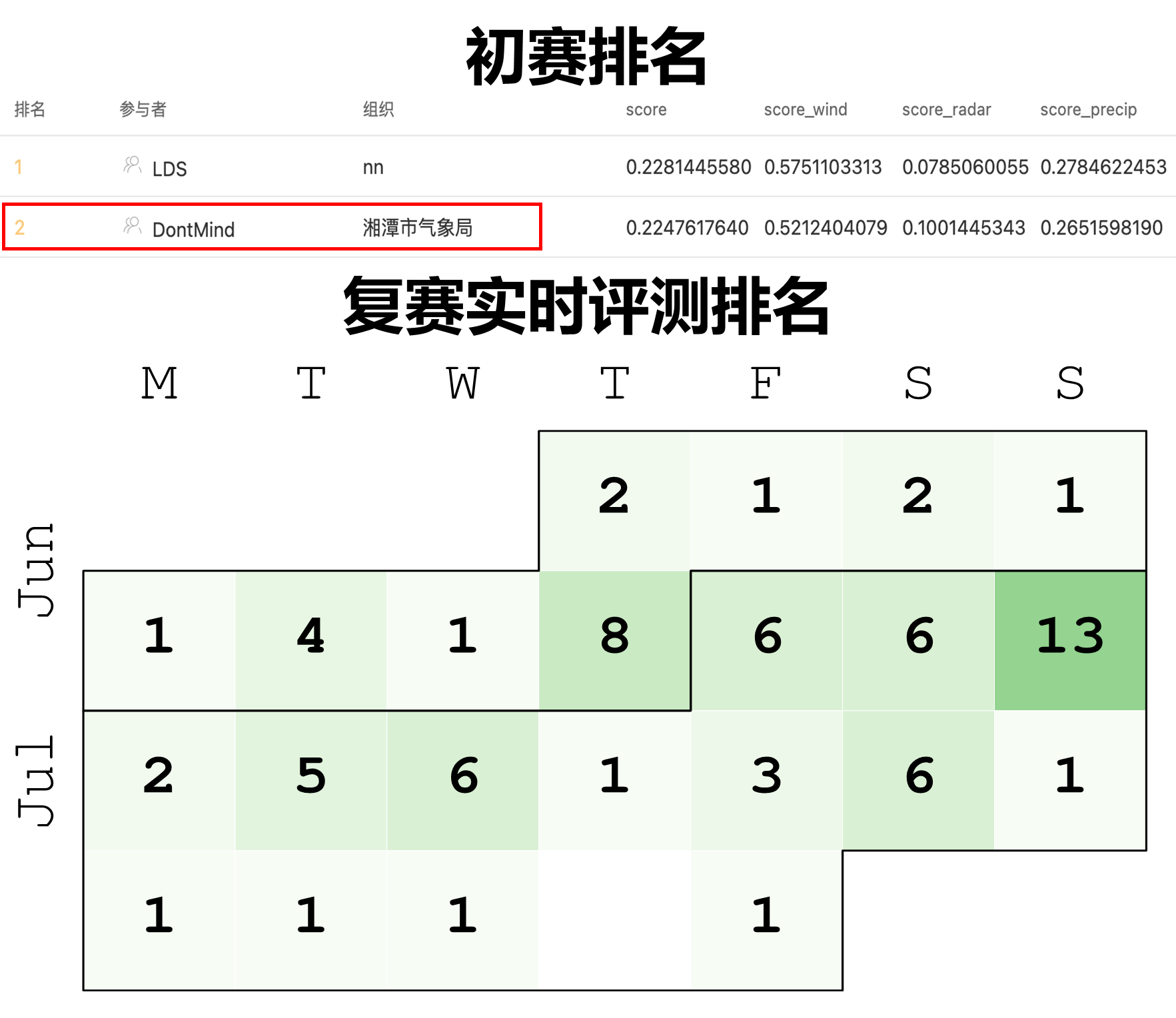
本次比赛我们初赛和复赛均为第二,其中复赛实时评测阶段22天大部分时段取得前6成绩,其中10天取得第1,模型总体表现较为稳定
查看更多内容,欢迎访问天池技术圈官方地址:2022江苏气象AI算法挑战赛亚军比赛攻略_DontMind队_天池技术圈-阿里云天池
这篇关于江苏气象AI算法挑战赛亚军比赛攻略_DontMind队的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








