Kannala-Brandt 鱼眼相机模型

本文主要是介绍Kannala-Brandt 鱼眼相机模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最近在学习 ORB-SLAM3 的源代码，并模仿、重构了相机模型的实现

在学习的过程中发现针孔相机 (Pinhole) 与鱼眼相机 (Fisheye) 都有畸变参数，但是鱼眼相机无法使用 cv::undistort 函数去畸变

在对鱼眼相机的深度归一化平面进行可视化后，发现鱼眼相机真的不需要去畸变

参考文献：A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses

相机基类模型

../logging.hpp 中主要调用了 glog 库，并定义了 ASSERT(expr, msg) 宏

基类 Base 初始化时需要输入 imgSize (图像尺寸)、intrinsics (相机内参)、distCoeffs (畸变参数)

#ifndef ZJSLAM__CAMERA__BASE_HPP
#define ZJSLAM__CAMERA__BASE_HPP#include <Eigen/Core>
#include <opencv2/opencv.hpp>
#include <sophus/se3.hpp>#include "../logging.hpp"namespace camera {typedef std::vector<float> Vectorf;enum CameraType {PINHOLE, FISHEYE
};class Base {protected:cv::Size mImgSize;Vectorf mvParam;cv::Mat mMap1, mMap2;   // 畸变矫正映射public:Sophus::SE3d T_cam_imu;typedef std::shared_ptr<Base> Ptr;explicit Base(const cv::Size imgSize, const Vectorf &intrinsics, const Vectorf &distCoeffs,const Sophus::SE3d &T_cam_imu = Sophus::SE3d()) : mImgSize(imgSize), mvParam(intrinsics), T_cam_imu(T_cam_imu) {ASSERT(intrinsics.size() == 4, "Intrinsics size must be 4")mvParam.insert(mvParam.end(), distCoeffs.begin(), distCoeffs.end());}virtual CameraType getType() const = 0;// 参数读取inline void setParam(int i, float value) { mvParam[i] = value; }inline float getParam(int i) const { return mvParam[i]; }inline size_t getParamSize() const { return mvParam.size(); }Vectorf getDistCoeffs() const { return {mvParam.begin() + 4, mvParam.end()}; }// 内参矩阵 K
#define GETK(vp, K) (K << vp[0], 0.f, vp[2], 0.f, vp[1], vp[3], 0.f, 0.f, 1.f)virtual cv::Mat getK() const { return GETK(mvParam, cv::Mat_<float>(3, 3)); };virtual Eigen::Matrix3f getKEig() const { return GETK(mvParam, Eigen::Matrix3f()).finished(); };// 3D -> 2Dvirtual cv::Point2f project(const cv::Point3f &p3D) const = 0;virtual Eigen::Vector2d project(const Eigen::Vector3d &v3D) const = 0;virtual Eigen::Vector2f project(const Eigen::Vector3f &v3D) const = 0;virtual Eigen::Vector2f projectEig(const cv::Point3f &p3D) const = 0;// 2D -> 3Dvirtual cv::Point3f unproject(const cv::Point2f &p2D) const = 0;virtual Eigen::Vector3f unprojectEig(const cv::Point2f &p2D) const = 0;// 去畸变virtual void undistort(const cv::Mat &src, cv::Mat &dst) = 0;// 绘制归一化平面 (z=1)void drawNormalizedPlane(const cv::Mat &src, cv::Mat &dst);
};
}#endif

鱼眼相机模型

因为在实现 C++ 的函数多态时，需要根据不同的输入值类型设计对应的计算过程 —— 但往往计算过程都是极其相似的，这给代码维护造成了麻烦

所以本文使用宏定义实现了这些计算过程

#ifndef ZJSLAM__CAMERA__KANNALA_BRANDT_HPP
#define ZJSLAM__CAMERA__KANNALA_BRANDT_HPP#include "base.hpp"namespace camera {// 最大视场角 (90)
#define KANNALA_BRANDT_MAX_FOV M_PI_2// 3D -> 2D
#define KANNALA_BRANDT_PROJECT_BY_XYZ(vp, p3D) \float R = this->computeR(atan2f(hypot(p3D.x, p3D.y), p3D.z)); \float phi = atan2f(p3D.y, p3D.x); \return {vp[0] * R * cosf(phi) + vp[2], vp[1] * R * sinf(phi) + vp[3]};#define KANNALA_BRANDT_PROJECT_BY_VEC3(vp, v3D) \float R = this->computeR(atan2f(hypot(v3D[0], v3D[1]), v3D[2])); \float phi = atan2f(v3D[1], v3D[0]); \return {vp[0] * R * cosf(phi) + vp[2], vp[1] * R * sinf(phi) + vp[3]};// 2D -> 3D
#define KANNALA_BRANDT_UNPROJECT_PRECISION 1e-6#define KANNALA_BRANDT_UNPROJECT_BY_XY(cache, p2D) \cv::Vec2f wxy = cache.at<cv::Vec2f>(p2D.y, p2D.x); \return {wxy[0], wxy[1], 1};class KannalaBrandt8 : public Base {protected:cv::Mat mUnprojectCache;void makeUnprojectCache();public:typedef std::shared_ptr<KannalaBrandt8> Ptr;explicit KannalaBrandt8(const cv::Size imgSize, const Vectorf &intrinsics, const Vectorf &distCoeffs,const Sophus::SE3d &T_cam_imu = Sophus::SE3d()) : Base(imgSize, intrinsics, distCoeffs, T_cam_imu), mUnprojectCache(mImgSize, CV_32FC2) {ASSERT(distCoeffs.size() == 4, "Distortion coefficients size must be 4")makeUnprojectCache();}CameraType getType() const override { return CameraType::FISHEYE; }// 3D -> 2Dfloat computeR(float theta) const;cv::Point2f project(const cv::Point3f &p3D) const override { KANNALA_BRANDT_PROJECT_BY_XYZ(mvParam, p3D) }Eigen::Vector2d project(const Eigen::Vector3d &v3D) const override { KANNALA_BRANDT_PROJECT_BY_VEC3(mvParam, v3D) }Eigen::Vector2f project(const Eigen::Vector3f &v3D) const override { KANNALA_BRANDT_PROJECT_BY_VEC3(mvParam, v3D) }Eigen::Vector2f projectEig(const cv::Point3f &p3D) const override { KANNALA_BRANDT_PROJECT_BY_XYZ(mvParam, p3D) }// 2D -> 3Dfloat solveWZ(float wx, float wy, size_t iterations = 10) const;cv::Point3f unproject(const cv::Point2f &p2D) const override { KANNALA_BRANDT_UNPROJECT_BY_XY(mUnprojectCache, p2D) }Eigen::Vector3f unprojectEig(const cv::Point2f &p2D) const override { KANNALA_BRANDT_UNPROJECT_BY_XY(mUnprojectCache, p2D) }// 去畸变void undistort(const cv::Mat &src, cv::Mat &dst) override { if (src.data != dst.data) dst = src.clone(); }
};
}#endif

与针孔类型相似的，鱼眼模型也有焦距 $f_x, f_y$ ，光心 $c_x, c_y$ ，以及畸变参数 $k_1, k_2, k_3, k_4$

借助这些参数，可以实现对世界坐标系下的点 $(X_c, Y_c, Z_c)$ 、像素坐标系下的点 $(x, y)$ 实现相互变换

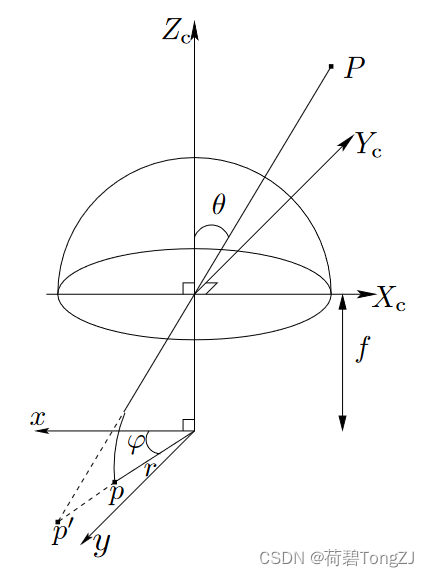
project (世界坐标 → 像素坐标)

$\theta = \arctan(\frac{\sqrt{X_c^2+Y_c^2}}{Z_c}), \psi = \arctan(\frac{Y_c}{X_c})$

$R(\theta)=k_1 \theta + k_2 \theta^3 + k_3 \theta^5 + k_4 \theta^7$

$x = f_x R \cos(\psi) + c_x, y = f_y R \sin(\psi) + c_y$

float KannalaBrandt8::computeR(float theta) const {float theta2 = theta * theta;return theta + theta2 * (mvParam[4] + theta2 * (mvParam[5] + theta2 * (mvParam[6] + theta2 * mvParam[7])));
}

unproject (像素坐标 → 世界坐标)

根据 project 的过程，可以由像素坐标计算得到 $R(\theta)$ ，并反向求得 $\theta$ ：

$X_c= \frac{x - c_x}{f_x}, Y_c = \frac{y - c_y}{f_y}$

$R(X_c, Y_c) = \sqrt{X_c^2 + Y_c^2 } \in [0, \infty)$

由于 $\theta$ 的取值是有上限的 (假设为 $\frac{\pi}{2}$ )，也就是说 $R_{max} = R(\frac{\pi}{2})$

所以当 $R(X_c, Y_c) > R_{max}$ 时，应当检查相机内参是否出错

使用梯度下降法使得 $l(\theta)=(R(\theta) - R(X_c, Y_c))^2=0$ ，以求解 $\theta$

由于 $l(\theta)$ 是一个凹函数，所以只要保证迭代量正负号正确即可

当求得 $\theta$ 时，便可以得到 $Z_c$ ：

$Z_c =R(X_c, Y_c) / \tan(\theta)$

而由于单目相机的深度没有什么意义，把 $(X_c / Z_c, Y_c / Z_c, 1)$ 作为对应的世界坐标

(这里使用缓存的方式实现 unproject)

void KannalaBrandt8::makeUnprojectCache() {float wx, wy, wz;for (int r = 0; r < mImgSize.height; ++r) {wy = (r - mvParam[3]) / mvParam[1];for (int c = 0; c < mImgSize.width; ++c) {wx = (c - mvParam[2]) / mvParam[0];wz = this->solveWZ(wx, wy);mUnprojectCache.at<cv::Vec2f>(r, c) = {wx / wz, wy / wz};}}
}float KannalaBrandt8::solveWZ(float wx, float wy, size_t iterations) const {// wz = lim_{theta -> 0} R / tan(theta) = 1float wz = 1.f;float R = hypot(wx, wy);float maxR = this->computeR(KANNALA_BRANDT_MAX_FOV);if (R > KANNALA_BRANDT_UNPROJECT_PRECISION) {float theta = KANNALA_BRANDT_MAX_FOV;if (R < maxR) {// 最小化损失: (poly(theta) - R)^2int i = 0;float e;for (; i < iterations; i++) {float theta2 = theta * theta, theta4 = theta2 * theta2, theta6 = theta4 * theta2, theta8 = theta6 * theta2;float k0_theta2 = mvParam[4] * theta2, k1_theta4 = mvParam[5] * theta4,k2_theta6 = mvParam[6] * theta6, k3_theta8 = mvParam[7] * theta8;e = theta * (1 + k0_theta2 + k1_theta4 + k2_theta6 + k3_theta8) - R;if (abs(e) < R * KANNALA_BRANDT_UNPROJECT_PRECISION) break;// 梯度下降法: g = (poly(theta) - R) / poly'(theta)theta -= e / (1 + 3 * k0_theta2 + 5 * k1_theta4 + 7 * k2_theta6 + 9 * k3_theta8);}if (i == iterations) LOG(WARNING) << "solveWZ(" << wx << ", " << wy << "): relative error " << abs(e) / R;}wz = R / tanf(theta);}return wz;
}

绘制深度归一化平面

深度归一化平面，即世界坐标点在 $Z_c = 1$ 平面上的投影，也就是一幅图像

基本思路就是，通过 unproject 获取深度归一化平面的边界，然后通过 project 获取平面上各个点对应图像中的位置

void Base::drawNormalizedPlane(const cv::Mat &src, cv::Mat &dst) {undistort(src, dst);cv::Mat npMap1 = cv::Mat(mImgSize, CV_32FC1), npMap2 = npMap1.clone();// 获取归一化平面边界 (桶形畸变)float x, y, w, h, W = mImgSize.width - 1, H = mImgSize.height - 1;x = this->unproject({0, H / 2}).x, y = this->unproject({W / 2, 0}).y,w = this->unproject({W, H / 2}).x - x, h = this->unproject({W / 2, H}).y - y;LOG(INFO) << "Normalized plane: " << cv::Vec4f(x, y, x + w, y + h);// 计算畸变矫正映射for (int r = 0; r < H; ++r) {for (int c = 0; c < W; ++c) {cv::Point2f p2D = this->project(cv::Point3f(w * c / W + x, h * r / H + y, 1));npMap1.at<float>(r, c) = p2D.x;npMap2.at<float>(r, c) = p2D.y;}}cv::remap(dst, dst, npMap1, npMap2, cv::INTER_LINEAR);
}

本文使用了 TUM-VI 数据集进行实验，Kannala-Brandt 相机的参数如下：

resolution: [512, 512]

intrinsics: [190.97847715128717, 190.9733070521226, 254.93170605935475, 256.8974428996504]

dist_coeffs: [0.0034823894022493434, 0.0007150348452162257, -0.0020532361418706202, 0.00020293673591811182]

(下面这段代码用了我自己写的其它东西，仅作参考)

void fisheye_test() {// 加载 TUM-VI 数据集 相机参数dataset::TumVI tumvi("/home/workbench/data/dataset-corridor4_512_16/dso");YAML::Node cfg = tumvi.loadCfg();auto cam(camera::fromYAML<camera::KannalaBrandt8>(cfg["cam0"]));// 加载图像列表, 读取第一张图像GrayLoader loader;dataset::Timestamps vTimestamps;dataset::Filenames vFilename;tumvi.loadImage(vTimestamps, vFilename);cv::Mat img = loader(vFilename[0]), dst1;// 显示原始图像, 以及去畸变后的图像cv::imshow("Origin", img);cam->drawNormalizedPlane(img, img);cv::imshow("NormalizedPlane", img);cv::waitKey(0);
}