本文主要是介绍3D投影变换(含透视投影Perspective Projection),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
透视投影变换将场景(世界空间)中的三维点投影到图像(图像/屏幕空间)中的二维点。
假设我们正在绘制一个仅由三维线段组成的模型,任务是将三维位置(在标准坐标系中表示为(x,y,z))坐标映射到图像中的坐标,以像素为单位表示,这是一个复杂的问题,因为它取决于许多不同的东西,包括相机的位置和方向、投影类型、视野和图像的分辨率。
对于所有复杂的转换,最好将其分解为几个简单转换。大多数图形系统都是通过四种变换来实现的:
#模型变换,通过模型矩阵实现,模型矩阵是一个转换矩阵,它可以平移、缩放和/或旋转您的对象,以将其放置在世界中的位置/方向。
#相机变换或眼睛变换(camera transformation),这是一种刚体变换,这个变换将相机放置在原点处,也就是从world space 变换到camera space。它只取决于相机的位置和方向,pose。
#投影变换(projection transformation),使待投影点从相机空间映射到x、y平面空间( range −1 to 1 )。这一过程只取决于所使用的投影变换类型。
#视口变换(viewport transformation)或窗口变换,将上面投影变换得到的单位图像矩形映射到生成图片像素坐标中的矩形。它只依赖于输出图像的大小和位置。
描述过程的各个阶段如图(图7.2)

视口变换(viewport transformation)
所有待投影点集都在下面的 canonical view volume 中,![]()
光线到volume 正上面后是一个square[−1, 1] * [−1, 1] ,想转换到一个nx by ny的图像矩形内,即
[-0.5,nx-0.5]*[-0.5,ny-0.5]矩形内

可以用下面的矩形缩放平移变换到另一个矩形的公式6.6,如下

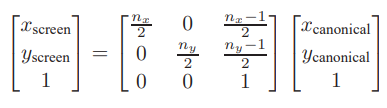
我们记这个视口变换矩阵为
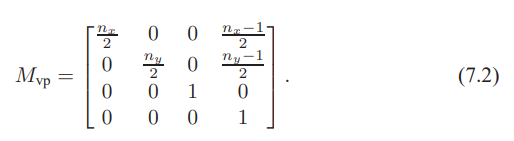
正交投影变换Orthographic Projection Transformation
正交投影变换是投影变换的一种,它是平行投影,所有的投影线都正交于投射面,保证投影前平行的线到投射面后依然平行。
这次保持和前面的视角相同,并且坐标轴和之前的canonical view volume对齐,只是待投影点集合不在限制在square[−1, 1] * [−1, 1]中,而是任意主轴垂直于投射面的立方体。

这样的条件下,要投影,只需要先把 orthographic view volume 变换到canonical view volume,就可以用前面视口变换实现投影。
空间中一个立方体到另一个立方体的变换,类似于公式6.6,

结合之后的投影如下
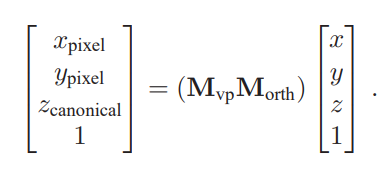
注释

相机变换The Camera Transformation
相机的位置和视角如果改变了,怎么办?比如相机的
,

答案把坐标系从globel (world)坐标系,换到相机坐标系。
因为我们已知相机的位置为e,视角为g,view-up为t,所以
在可以建立相机坐标系,通过下面公式
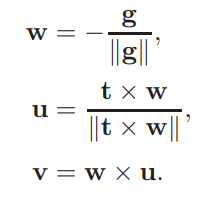
此时,想要利用前面我们推导的,只需要将
xyz-coordinates 变换到uvw-coordinates.即可。
下面看看2D坐标系怎么变换,
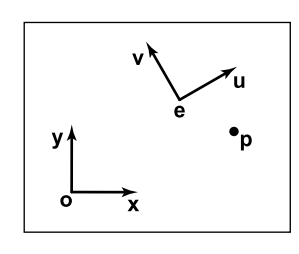
已知
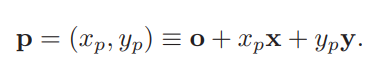
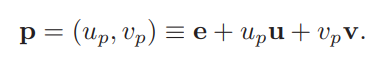
有
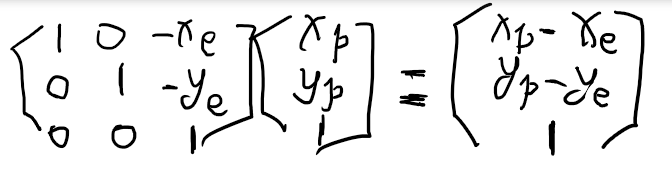
这是pe在xyo坐标下的向量, 投影到uve坐标,只需要
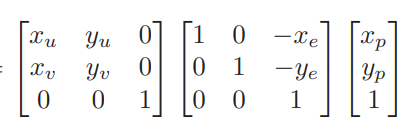
2D推广到3D
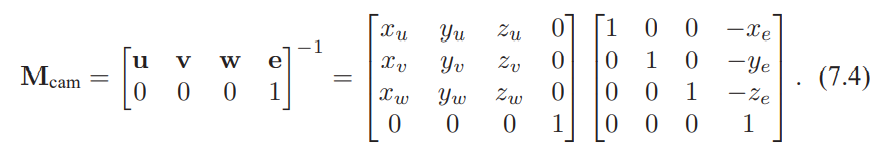
下面使3D线段投影的伪代码:

3D projections use the primary qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element.
透视投影(Perspective Projection)
每次顶点着色器运行结束时,OpenGL 期望坐标在特定范围内,任何超出此范围的坐标都被剪裁掉,剩余的坐标被投影到屏幕上。
剪裁clip到一个视锥体

投影视锥体内的坐标到标准设备坐标

具体怎么投影?

方法是,将物体空间坐标的点直接向眼睛方向投影,画在投射线与View Plane/Near Plane相交的地方。
基本原理图

希望能写出一个实现上述变换的矩阵,难,因为目前建立的矩阵机制并没有除z的运算。再回来看一看

在图7.8所示的2D示例中,我们尝试通过矩阵变换实现透视投影,如下:

2D推广到3D


P不是唯一的透视矩阵,有许多矩阵可以作为透视矩阵,可是其他的都会非线性地扭曲z坐标。而我们的这个特定的矩阵P具有如图7.11和7.12所示的特点,即它使得在(z=n)上的点完全不受影响,同时“挤压”在(z=f)平面上的点,使得它们在x和y中以适当的比例缩放。通过对一个点(x,y,z,1)的测试,既可以知道P的作用效果:(注释:第四行1是点的分母或缩放比例)

看到没,成功的实现了x,y维度的n/z缩放,也就是,实现了z除的操作。
另外映射后,沿着z轴方向的点顺序和之前保持一致。所以这个P是一个很好的透视变换矩阵。
好了我们现在找到了P,可以映射the perspective view volume -> the orthographic view volume(which is an axis-aligned box).
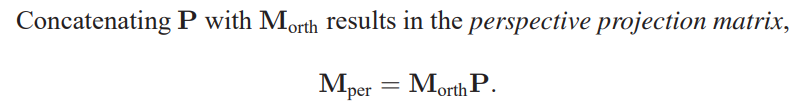
下面是线段从perspective viewing中投影到image的算法:

代码实战
可以在 GLM 中创建透视投影矩阵,把eye space的坐标变换到clip space的坐标,如下所示:
glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f); glm::perspective 创建一个大的视锥可视空间,视锥之外的任何内容会被裁剪。视锥平截头体可以被视为一个形状不规则的盒子,盒子内的每个坐标都将映射(保留)到clip空间中。生成的顶点分配给顶点着色器中的gl_Position,然后 OpenGL 将自动执行透视分割,完成到透视到屏幕的后续操作。
视锥平截头体的图像如下所示:

它的第一个参数FOV设置视角空间有多大。对于逼真的视图,它通常设置为 45 度,但对于更多厄运风格的结果,您可以将其设置为更高的值。
第二个参数设置viewport/near plane的纵横比。
第三个和第四个参数设置视锥体的近平面和远平面。我们通常设置近距为0.1,远距为100.0。将渲染近平面和远平面之间以及截锥体内部的所有顶点。
这篇关于3D投影变换(含透视投影Perspective Projection)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









