CSAPP | Floating Point

本文主要是介绍CSAPP | Floating Point，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

CSAPP | Floating Point

$b_i$ $b_{i-1}$ … $b_2$ $b_1$ $b_0$ $b_{-1}$ $b_{-2}$ $b_{-3}$ … $b_{-j}$
$S={\sum }_{k=-j}^i{b}_k\times 2^k$

IEEE Standard 754

浮点数表示方法

$v=(-1{)}^s\times M\times 2^E$
符号位 Sign: 0 表示正，1 表示负。
尾数 Significand M: $\in [1.0,2.0)$
阶码 exponent: E 对浮点数加权，权重为 2 的 E 次幂。

浮点数分为三个域：符号、阶码、 尾数
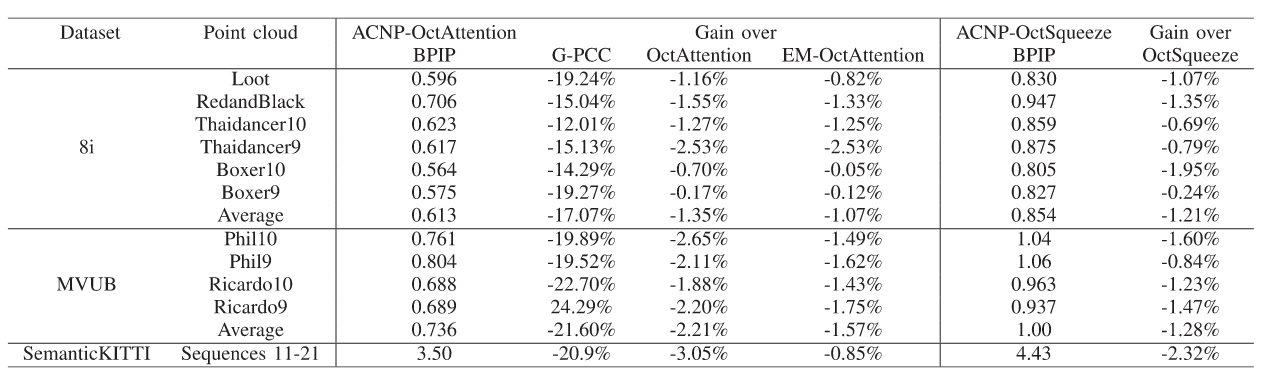
sign (1 bit) | exponent (e bit) | fraction(or mantissa) (f bit)

sign 直接编码符号 s
k 位阶码字段 $exp=e_{k-1}...e_1{e}_0$ 编码了 E(但是不等同于 E)
n 位小数字段 $frac=f_{n-1}...f_1{f}_0$ 编码了 M(但是不等同于 M)

规格化值

1.exp $\ne$ 000…0 and exp $\ne$ 111…1

2.阶码字段以 biased(偏置) 形式表示，E = Exp - Bias，Exp 为无符号数，Exp 的范围为 $00000001\sim 11111110$ 即 $1\sim 254$。Bias 为 $2^{k-1}-1$，由此产生的指数取值范围，单精度为 $-126\sim +127$，双精度为 $-1022\sim +1023$

3.小数字段 frac 被解释为描述小数值 f，$f\in [0,1)$, 二进制表示为 $0.f_{n-1}...f_1{f}_0$。尾数定义为 $M=1+f$。可以把 M 看作为二进制表示为 $1.f_{n-1}...f_1{f}_0$。

4.对于尾数，我们可以“抛掉”小数点左边的 1，只看右侧。M 最小的时候 frac = 000…0(M = 1.0)，M 最大的时候 frac = 111…1(M = 2.0 - $\epsilon$，也就是 1.111…1)
IEEE754浮点数阶码为什么需要偏置bias

Single precision: 32 bits

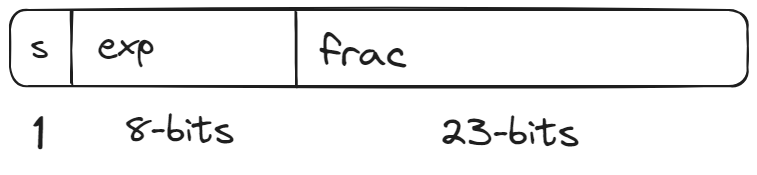
Double Precision: 64 bits

Example

对于浮点数 F = 15213.0
$15213_{10}$
$=11101101101101_2$
$=1.1101101101101_2\times 2^{13}$

Significand

$M=1.1101101101101_2$
$frac=11011011011010000000000_2$(23 bits)

Exponent

$E=13$ 因为 2 的幂是 13
$Bias=127$ 因为 float 单精度表示，k = 8, $Bias=2^{k-1}-1=2^7-1=127$
$Exp=140=10001100_2=E+Bias$

Result

$01000110011011011011010000000000_2$
从左到右分别为 s exp frac

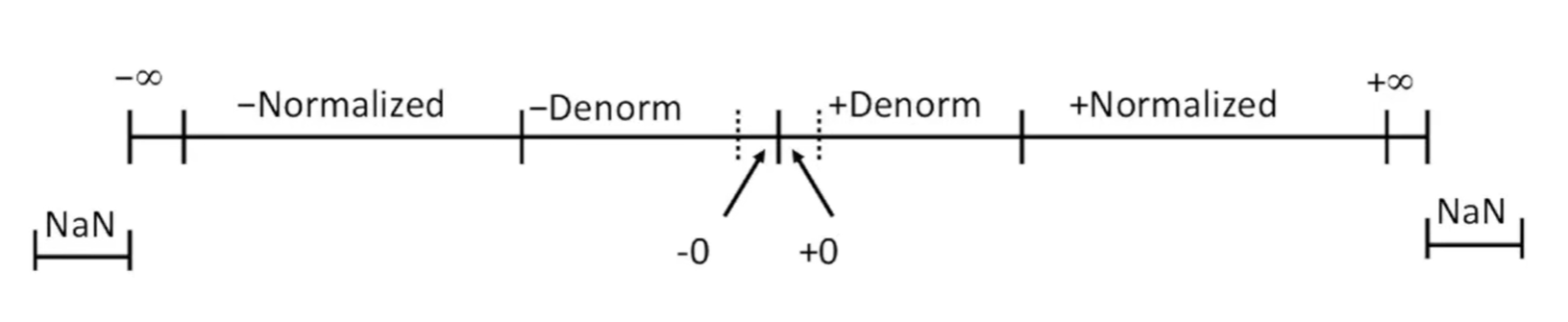
非规格化值

如果使用规格化数，总是使 $M\ge 1$，就无法表示 0。而 +0.0 的浮点表示位模式为全 0。符号位为 0，阶码字段为 0，是一个非规格化值。然而此时 M = f = 0。如果符号位为 1，那么就是 -0.0。

1.exp = 000…0 成立

2.E = 1 - Bias

3.M = 0.xxx…x

特殊的值

$exp=\mathrm{111...1},frac=\mathrm{000...0}$ 代表无穷大
$exp=\mathrm{111...1},frac\ne \mathrm{000...0}$ $NaN(notanumber)$ E.g. sqrt(-1)

Visualization: Floating Point Encodings

对于 8 位浮点数：
$k=4,Bias=2^3-1=7,E=1-Bias=1-7=-6$

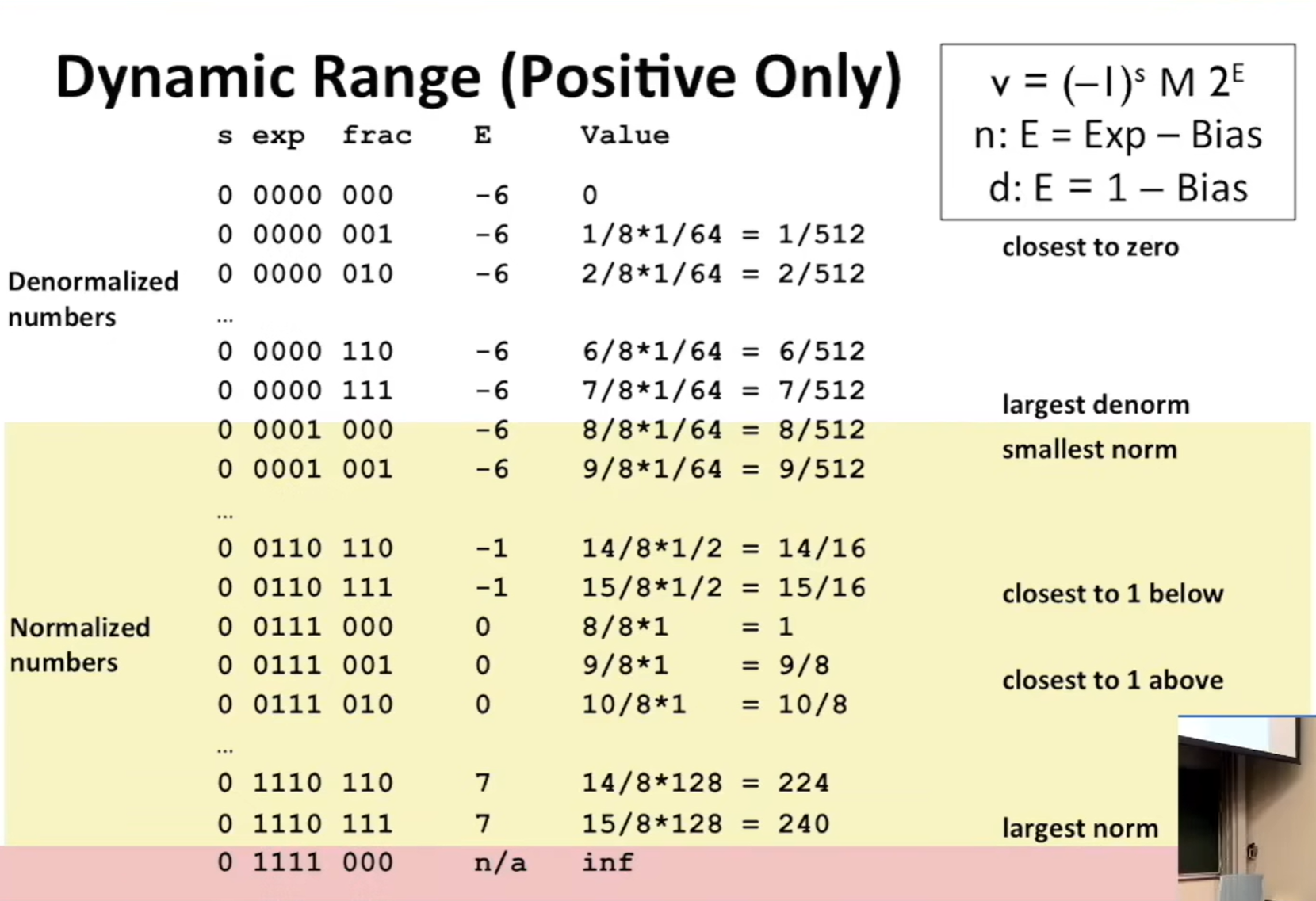
对于非规格化值：
$E=1-Bias$
0 0000 000，M = 0，$0\times 2^{-6}=0$
0 0000 001, $M=1\times 2^{-3}=\frac{1}{8},\frac{1}{8}\times \frac{1}{2^6}=\frac{1}{512}$
…
0 0000 111 为非规格化值所能表示的最大值
对于规格化值：
$E=exp-Bias$
0 0001 000 此时 $exp=1,E=exp-Bias=1-7=-6,frac=000,M=1.000$，这是最小的规格化值。
…

Rounding

IEEE 现在有四种舍入方式，分别为 向零舍入、向下舍入、向上舍入、就近舍入(默认)

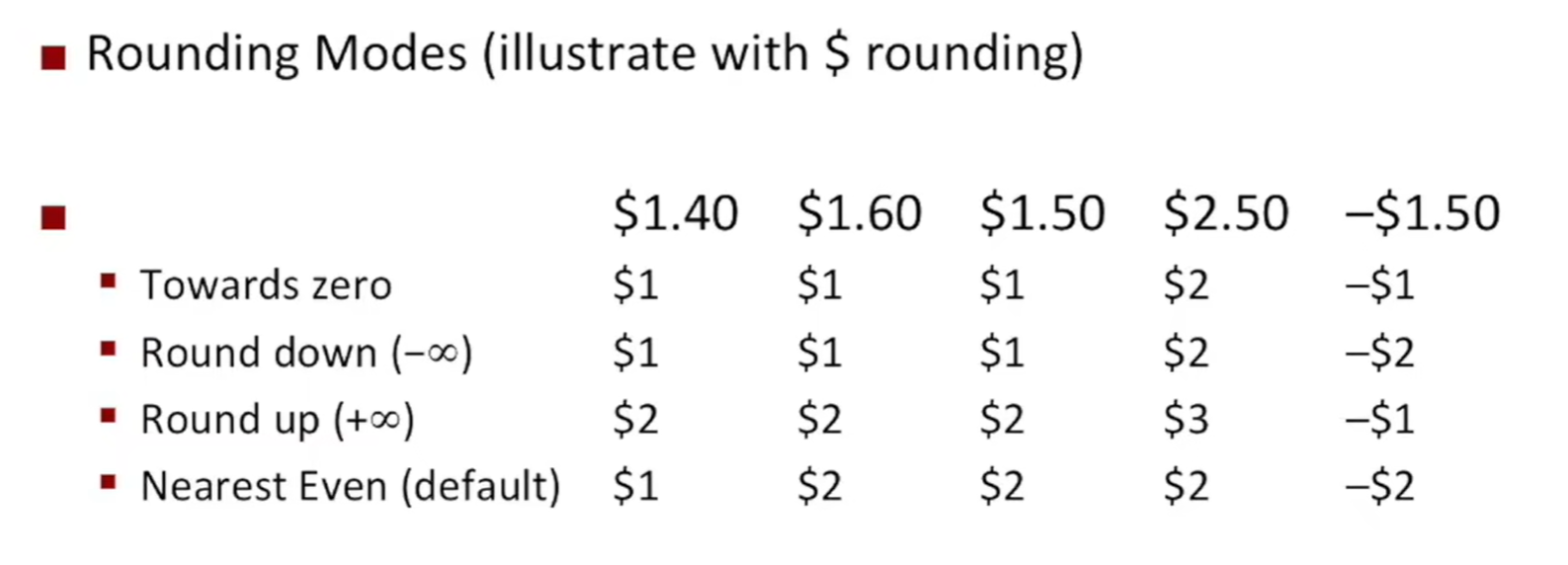
如何理解就近舍入?

当为中间数，要向最近的偶数(舍入后保留的最低有效位是偶数)舍入。

对于 7.8950000，9 是一个奇数，所以向上舍入。
对于 7.8850000，8 是一个偶数，所以向下舍入。

二进制数截断

对于 $10.11100_2$ 如果直接截断，则为 10.11 是个奇数，所以应该加上 0.001

乘法

$((-1{)}^{s1}\times M1\times 2^{E1})\times ((-1{)}^{s2}\times M2\times 2^{E2})$
$Signs:s1\oplus s2$
$SignificandM:M1\times M2$
$ExponentE:E1+E2$

如果 M $\ge$ 2，则须有右移位同时增加指数，来让尾数在 1 和 2 之间。
如果 E 超出范围，则会溢出到无穷大。
如果 M 有太多位，则需要就近舍入。

(3.14 + 1e10) - 1e10 = 0
3.14 + (1e10 - 1e10) = 3.14
1e20 $\ast$ (1e20 - 1e20) = 0.0

Questions

int x = ...;
float f = ...;
double d = ...;x == (int)(float) x; // False, 在浮点数的 frac 区域没有足够的位来表示 int,会舍入
x == (int)(double) x; // True
f == (float)(double) f; // True
d == (double)(float) d; // False
f == -(-f); // True
2 / 3 == 2 / 3.0 // False, 2/3=0, 2/3.0 是一个浮点数
d < 0.0 -> ((d * 2) < 0.0) // Yes, 即使 d * 2 溢出到负无穷大，也是小于 0
d > f -> -f > -d // Yes
d * d >= 0.0 // Yes
(d + f) - d == f // No

这篇关于CSAPP | Floating Point的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---