本文主要是介绍现代计算机图形学笔记(七)——重心坐标、应用纹理Mipmap,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
重心坐标(Barycentric Coordinates)
上几节课都提到了在三角形内部做插值,为了研究此问题,我们引入重心坐标(Barycentric Coordinates)。重心坐标的应用很广泛,如在像素着色器(Fragment shader)中我们已知三角形三个顶点的法向量,去插值求解三角形内部每个像素的法向量;在纹理映射时,我们已知三角形三个顶点在纹理坐标中的 u , v u,v u,v值,去插值获得三角形内部纹理坐标的值。
我们定义三角形坐标系(coordinate system for triangles),如下图
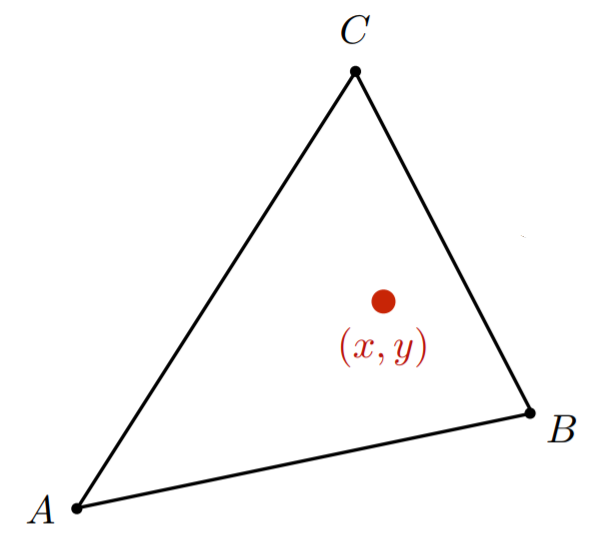
我们有一个三角形 △ A B C \triangle ABC △ABC,其三个点的坐标 A , B , C A,B,C A,B,C已知,则对于三角形所在平面的任意一点都可以由该三角形的三个坐标的线性组合表示出来
( x , y ) = α A + β B + γ C α + β + γ = 1 (1) (x,y)=\alpha A+\beta B+\gamma C \\ \alpha +\beta +\gamma =1 \tag{1} (x,y)=αA+βB+γCα+β+γ=1(1)
而 ( α , β , γ ) (\alpha,\beta,\gamma) (α,β,γ)称为点 ( x , y ) (x,y) (x,y)的重心坐标。这里,如果 α , β , γ \alpha ,\beta ,\gamma α,β,γ均大于0,则表示的点一定在 △ A B C \triangle ABC △ABC内部。
如下图所示,我们可以用三角形的面积比例定义三角形内部任意一点。
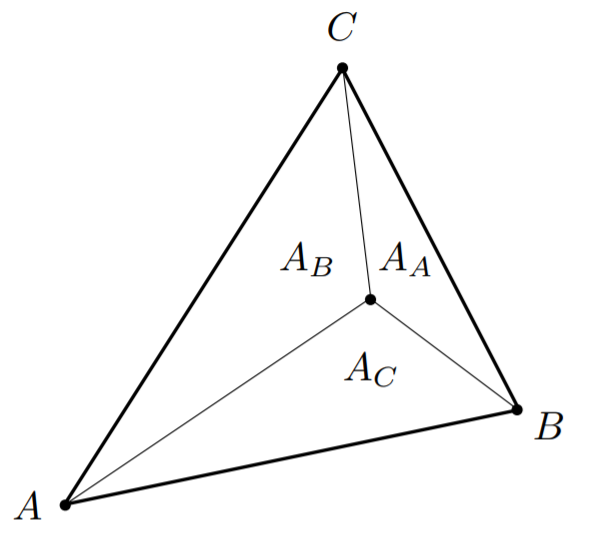
α = A A A A + A B + A C β = A B A A + A B + A C γ = A C A A + A B + A C (2) \alpha=\frac{A_A}{A_A+A_B+A_C}\\ \beta=\frac{A_B}{A_A+A_B+A_C}\\ \gamma=\frac{A_C}{A_A+A_B+A_C} \tag{2} α=AA+AB+ACAAβ=AA+AB+ACABγ=AA+AB+ACAC(2)
其中 A A , A B , A C A_A,A_B,A_C AA,AB,AC
这篇关于现代计算机图形学笔记(七)——重心坐标、应用纹理Mipmap的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







