本文主要是介绍论文笔记3《基于信息增益和最小距离分类的决策树改进算法》,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
2013年《科学技术与工程》期刊
部分摘要:改进后的算法针对决策树在分类过程中遇到的训练集中存在相同属性集,但属于不同类别的实例的情况,不再采用多数表决法判断叶结点的类别,而是采用基于信息增益的属性约简和最小距离分类的新方法进行类别的判断。
算法改进:

算法描述:
(i) 先构造ID3决策树,但在构造的过程中对于具有相同属性集属于不同类别的实例,暂时用null标注它的类别;
(ii) 对决策树中所有类别为的叶结点,调用基于信息增益的最小距离分类器对它们进行重新分类。
实验结果:
数据:
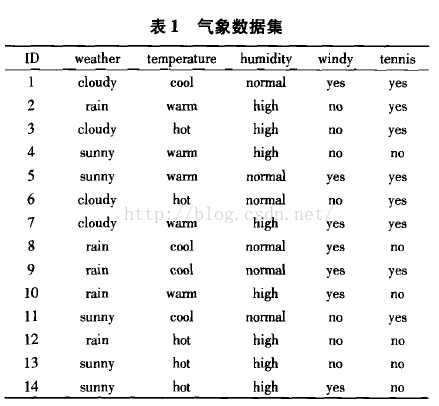
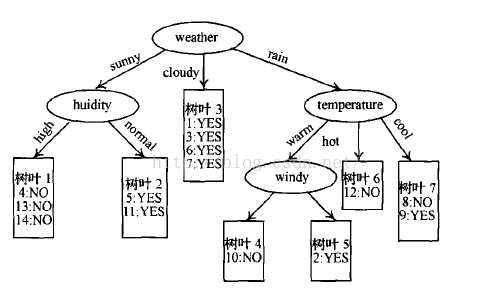
从图中可以看出树叶1-6都是纯叶结点,树叶7不是纯叶结点。训练集中实例8,9属于树叶7,而实例8和实例9具有相同属性集,但属于不同类别, 下面将采用基于信息增益的最小距离分类来决定树叶的类别。
(1) 计算属性的信息增益并将信息增益归一化处理后结果为:
InfoGain(weather)=0.56
InfoGain(temperature)=0.11
InfoGain(humidity)=0.31
InfoGain(windy)=0.02
(2) 就算叶子7和其他叶节点的距离:
树叶7的中心结点K的各属性值为:(weather=rain,temperature=cool,humidity=normal,windy=yes,tennis=null);
树叶6的中心结点K的各属性值为:(weather=rain,temperature=hot,humidity=high,windy=no,tennis=no);
树叶5的中心结点K的各属性值为:(weather=rain,temperature=warm,humidity=high,windy=no,tennis=yes);
树叶4的中心结点K的各属性值为:(weather=rain,temperature=warm,humidity=high,windy=yes,tennis=no);
…其他同理
则距离D(K,)==0.663;D(K,)=0.663;D(K,)=0.648;
…
通过比较可知与最近的应该是,因此树叶7的类别应该与树叶4一样为no。
这篇关于论文笔记3《基于信息增益和最小距离分类的决策树改进算法》的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






