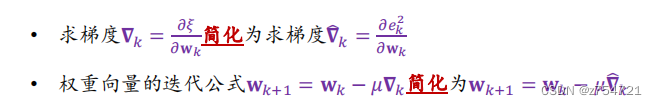本文主要是介绍自适应信号处理基础及应用——DSP学习笔记五,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
-
本专栏的图片内容都来自于老师讲课的PPT,本篇博客只是我个人对于上课内容的知识结构分析和梳理。
-
导论
-
自适应系统的定义、特征、形式、举例
-
特征
-
非自适应系统
-
• 固定参数的设计方法
-
• 假定事先知道了一切可能的输入条件;在这些条件下怎样动作;选择了一个性能准则;进而选择了一个看起来最好的系统
-
-
自适应系统
-
能够自动地适应变化的环境与变化的系统要求
-
• 能够通过训练改变系统结构,以完成特定的滤波或判决任务
-
• 通常不需要精确的系统设计,而是能“自行设计”
-
• 在有限的范围内能够自我检测,适应于一定类型的内部故障
-
• 通常被描述成非线性时变系统
-
• 通常比较复杂、难以分析
-
-
-
一般形式:开环、闭环(无论那种形式,系统的处理器都必须是可调节的)
-
-
-
自适应线性组合器
-
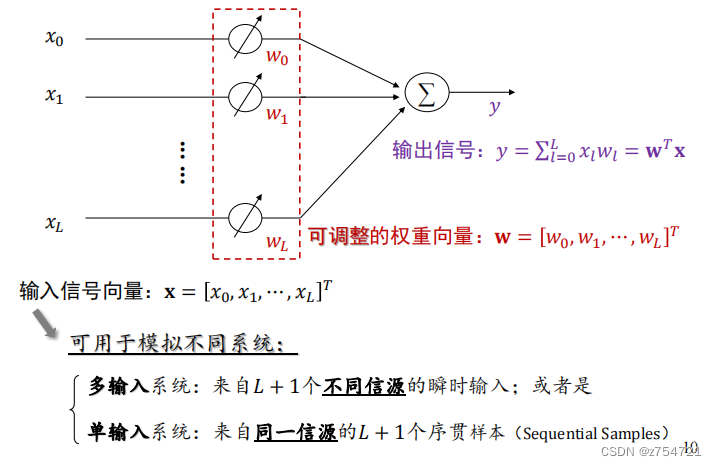
一般形式
-
单输入横向滤波器形式

-
-
性能函数与最小均方误差
-
这里引入误差信号,他作为检验滤波器性能的指标,是调制权重向量使这个指标最小化,我们常用的事均方误差,挤兑瞬时平方误差求期望。
-

-

-
画出这个均方误差,就可以得到这么一个曲面,我们称这个抛物面为误差曲面。通过表达式,可以知道MSE是权重向量W的二次函数,我们要使MSE最小,目标就是思考如何得到最优的权重向量W。下面介绍的方法,就是从解决这一问题的角度出发的
-

-

-
-
-
-
性能曲面的搜索
-
引言:前面我们得到,如果输入信号𝑥与期待响应𝑑都是统计平稳,那么自适 应线性组合器的均方误差MSE是权重向量𝐰的二次函数然而,在很多实际应用中,二次型性能曲面的参数(𝐑, 𝐩)是未知的,其解析表达式不能得到因此,需要开发一种搜索性能曲面的方法,迭代地寻找或逼近最优权重向量𝐰∗
-
基于梯度的方法:
-
牛顿法
-

-

-
用性能函数替换f(w),即可得到求解性能函数最小值的迭代公式
-
-
 优点:收敛速度较快
优点:收敛速度较快 -
缺点:
-
对于一次和二次导数未知的情况,需要作相应的估计,较复杂
-
对于初始点远离最优解的情况,搜索也有可能不成功
-
对于不是二次形式的函数(性能曲面),从初始点出发,有时候搜索不到最优解
-
-
-
梯度下降法:与牛顿法不同,梯度下降法:每一步对权重向量的调整,都是在梯度方向
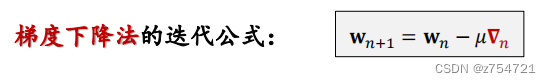
-
最小均方算法(LMS算法)
-
-
-
-
-
应用
-
系统辨识
-
噪声消除
-
信号增强
-
系统反演建模
-
这篇关于自适应信号处理基础及应用——DSP学习笔记五的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!