Dropout Feature Ranking for Deep Learning Models

本文主要是介绍Dropout Feature Ranking for Deep Learning Models，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘要

深度神经网络( deep neural networks，DNNs )在多个领域取得了最新的研究成果。不幸的是，DNNs因其不可解释性而臭名昭著，从而限制了其在生物和医疗保健等假说驱动领域的适用性。此外，在资源受限的环境下，设计依赖更少信息特征的测试是至关重要的，这将在合理的预算范围内实现高精度的性能。我们旨在通过提出一种新的面向深度学习的通用特征排序方法来弥合这一差距。我们展示了我们的简单而有效的方法在静态和时间序列场景中，在从分类到回归的任务中，在两个模拟和5个非常不同的数据集上，与8个“草人”、经典和深度学习的特征排序方法进行了比较。我们还说明了我们的方法在药物反应数据集上的使用，并表明它识别了与药物反应性相关的基因。

简介

深度神经网络( Deep Neural Networks，DNNs )已经开始在生物学和医疗保健领域崭露头角，包括基因组学( Xiong et al . , 2015)、医学影像( Esteva et al , 2017)、EEG ( Rajpurkar et al , 2017)和EHR ( Futoma et al , 2017)。然而，DNNs是黑盒模型，因其不可解释性而臭名昭著。在生物学和医疗保健领域，为了推导出可以通过实验验证的假设，提供关于哪些生物学或临床特征驱动预测的信息是至关重要的。所需的数据收集可能非常昂贵，因此，在合理的预算范围内生成收集最有效数据的实验设计也很重要。因此，对de进行特征排序有很强的需求。我们旨在通过提出一种新的面向深度学习的通用特征排序方法来弥合这一鸿沟。
在这项工作中，我们提出了通过变分dropout ( Gal et al , 2017)对特征进行排序。Dropout是一种常用于正则化神经网络的有效技术，通过随机移除隐藏节点值的子集并将其设置为0。在这项工作中，我们在输入特征层上使用Dropout概念，并优化相应的特征级Dropout率。由于每个特征都是随机移除的，因此我们的方法产生了类似于特征装袋( Ho , 1995)的效果，并且能够比其他非装袋方法(如LASSO )更好地对相关特征进行排序。我们将我们的方法与随机森林( RF )，LASSO，ElasticNet，Marginal排序和几种导出重要性的技术在DNN中，如深度特征选择和各种启发式进行了比较。我们首先在2个仿真数据集上进行了测试，表明我们的方法能够在非线性特征交互中，特别是在重要特征之间，对特征进行正确的排序。然后我们在4个真实世界的数据集上进行了测试，并表明我们的方法在深度神经网络中相同的特征数量下具有更高的性能。然后我们在多变量临床时间序列数据集上进行了测试，并表明我们的方法在循环神经网络设置中也能与其他方法竞争或优于其他方法。最后，我们使用先前提出的变分自编码器( Variational Autoencoder，VAE ) ( Kingma和韦林, 2013)在真实世界的药物反应预测问题上测试了我们的方法。

最近工作

许多先前提出的解释DNNs的方法集中于解释一个决策(例如在图像中指定一个特定的分类标签) (针对手边的一个具体例子( e.g . (西蒙尼扬et al , 2013 ; Zeiler and Fergus , 2014 ;里韦罗et al , 2016 ; Zhou et al , 2016 ; Selvaraju et al , 2016 ; Shrikumar et al , 2017 ; Zintgraf et al , 2017 ; Fong and韦达尔迪, 2017 ; Dabkowski and Gal , 2017 ) ) )。在这种情况下，一种方法的目的是确定给定图像的哪些部分使分类器认为该特定图像应该被分类为狗。不幸的是，这些方法不容易用于特征选择或排序的目的，其中特征的重要性应该在整个数据集中收集。
一些工作提到了使用变分dropout来实现更好的性能( Gal et al , 2017) Kingma et al ( 2015 )，对dropout进行贝叶斯解释( Maeda , 2014)，或者压缩模型架构(莫尔恰诺夫等, 2017)。这些工作侧重于调整辍学率以自动获得最佳性能，但没有考虑将其应用于特征排序问题。
Li等人( 2016 )提出了深度特征选择( Deep Feature Selection，Deep FS )。Deep FS在网络中添加了另一个隐藏层，每个输入节点有一个连接到这个隐藏层(与输入大小相同)，并在这个层上使用一个1惩罚。这些层之间的权重被初始化为1，但由于它们不受[ 0、1 ]的限制，它们可以成为大的正值和负值。因此，这个附加层可以放大特定的输入，并且需要在原有的网络架构内进行平衡。此外，使用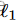 ' 1 惩罚可以防止Deep FS选择相关特征，这在许多生物和健康应用中非常重要。
最后，几部著作还针对临床环境下的口译特点进行了分析。Che等人( 2015 )使用梯度提升树( Gradient-Boosted Trees )在医疗数据集上模拟循环神经网络以达到可比的性能。Nezhad等人( 2016 )通过自动编码器和随机森林来解释临床特征。Suresh等人( 2017 )使用循环神经网络来预测临床数据集，并在我们的设置中使用名为" Mean "的排序启发式。这些方法依赖于额外的决策树结构来学习特征，或者使用在我们的实验中排名性能较弱的启发式。

方法

3.1 Variational dropout

Dropout (斯里瓦斯塔瓦等, 2014)是神经网络最有效、应用最广泛的正则化技术之一。其机制是为神经网络中的每个隐藏单元注入一个乘性伯努利噪声。具体来说，在前向传递过程中，对于第j层的每个隐藏单元k，采样一个dropout掩码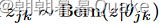 zjk⋅Bern ( z | θjk ) 。然后将原始隐藏节点值hjk乘以该掩码 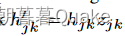h′jk = hjkzjk ，该掩码将隐藏节点值随机设置为hjk或0。
变异Dropout ( Maeda , 2014)将Dropout rate θ作为一个参数进行优化，而不是将其作为一个固定的超参数。对于一个神经网络f ( x )，给定一个大小为M的小批量(从训练集中抽取N个样本)和一个dropout掩码z，对dropout进行变分解释后得到的损失目标函数可以写为：
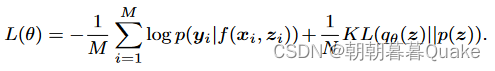
在这里插入图片描述
这里，zi┐qθ ( z )，其中q θ ( z )是变分掩码分布，p ( z )是先验分布.

3.2 使用Variational dropout进行特征排序

图1显示了我们的方法。为了分析哪些特征对于给定的预训练模型M正确预测其目标变量y是重要的，我们引入了Dropout Feature Ranking ( Dropout FR )方法。在我们的方法中，我们在M的输入层中加入了变分dropout正则化。为了达到最小的损失，Dropout FR模型应该学习小的dropout率，对于被分析模型M正确的目标预测很重要的特征，而对于其他不重要的特征，则增加dropout率。具体来说，给定D个特征，我们设定一个变量掩码分布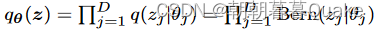 q θ ( z ) =∏Dj = 1q ( zj | θj ) =∏Dj = 1Bern ( zj | θj )
为完全因式分解分布。这给了我们一个基于特征的辍学率θ j，其大小表示特征j的重要性。我们不在式( 1 )中使用KL ( qθ ( z ) | | p ( z ) )对dropout分布q θ ( z )进行正则化，而是直接对现有特征数量(特征不丢失)进行惩罚。这样就避免了事先设定辍学率p ( z )的需要，与线性回归(墨菲, 2012)的’ 0惩罚对齐。因此，我们的损失函数可以写为：
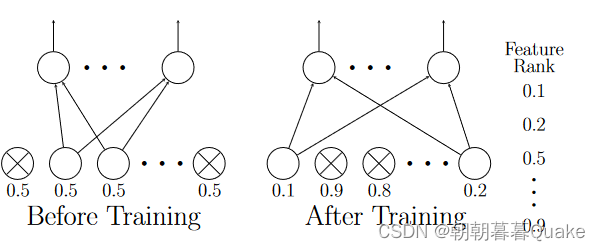
在这里插入图片描述
图1：Dropout特征排序图。训练前( Left )，每个特征的退学率初始化为0.5。经过训练( Right )后，每个特征得到不同的丢弃率。然后，我们根据辍学率的大小对所有特征进行排序- -幅度越低，排序越高。

我们不在式( 1 )中使用KL ( qθ ( z ) | | p ( z ) )对dropout分布q θ ( z )进行正则化，而是直接对现有特征数量(特征不丢失)进行惩罚。这就避免了事先设定辍学率p ( z )的需要，与线性回归(墨菲, 2012)的’ 0惩罚对齐。因此，我们的损失函数可以写为：
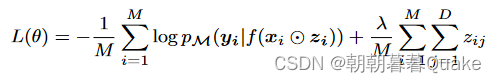
在这里插入图片描述
式中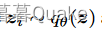： zi⋅qθ ( z )
，λ由交叉验证确定。
具体松弛为了优化L ( θ )关于参数θ，我们需要通过离散变量z向后传播。我们采用与Gal et al . ( 2017 )相同的方法来优化我们的辍学率。具体来说，我们不是对离散的伯努利变量进行采样，而是对混凝土分布( Jang et al . , 2016 ;麦迪森等, 2016)进行温度t的采样，t的值在0到1之间。该分布将大部分质量置于0和1中，以近似离散分布。伯努利分布Bern ( z | θ )的具体松弛" z "为：
在这里插入图片描述
式中：u⋅Uniform( 0、1 )。我们将t固定为0.1，发现它在我们的所有实验中都是有效的。与传统的REINFORCE估计器(威廉姆斯, 1992)相比，这种具体的分布具有更低的方差和更好的性能(数据未显示)，因此我们在所有的实验中都应用了它。
退火我们采用了退火技巧，以避免模型在完全优化之前被惩罚过重。具体来说，在优化过程中，我们在最初的几个阶段将λ从0线性地增加到指定的值。这与VAE中的KL退火技巧( Bowman et al , 2015)类似。
与强化学习的关系我们的方法可以看作是一种基于策略梯度的方法( Sutton et al , 2000) (强化学习技术之一)，应用于特征选择设置。从这个角度来看，我们的策略是因式分解的伯努利分布，奖励由目标的对数概率和使用特征的数量组成。我们优化了使用 2P 组合在这个大型特征空间中输出最佳特征组合的策略，其中 P 是特征总数。为了获得特征方面的解释，我们采用因式分解伯努利分布来获得每个特征的重要性值作为我们的排名。