代码随想录算法训练营第20天 |654.最大二叉树、 617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树

本文主要是介绍代码随想录算法训练营第20天 |654.最大二叉树、 617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

链接: 654.最大二叉树
链接: 617.合并二叉树
链接: 700.二叉搜索树中的搜索
链接: 98.验证二叉搜索树

自己看到题目的第一想法

654.最大二叉树：明确了是递归法，知道应该使用三部曲，首先确定递归函数的参数和返回类型，构建二叉树返回类型是void，参数为数组；终止条件应该是数组使用完成；递归函数内的逻辑是前序遍历。
700.二叉搜索树中的搜索：递归，前序遍历

看完代码随想录之后的想法

654.最大二叉树：首先整体思路是递归，三部曲，递归函数输入参数是数组，返回值应当是根节点，而不是空，这点我自己第一想法是错误的，终止条件应该是数组的长度为1，因为数组长度为1说明此时已经是在叶子节点了，递归函数内部逻辑是前序遍历，先根据输入数组的最大值构造根节点，因为是数组，根据数组的特点可以根据最大值索引下标划分成左右子数组从而分别对左子树和右子树进行构造。另外可以回顾一下昨天的题目。

class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return Construct(nums,0,nums.length-1);}public TreeNode Construct(int[] nums,int leftIndex,int rightIndex){if(leftIndex>rightIndex){return null;}//求数组的最大值索引下标int maxIndex =leftIndex;for(int i=leftIndex+1;i<=rightIndex;i++){if(nums[maxIndex]<nums[i]){maxIndex=i;}}//构建中间节点TreeNode root = new TreeNode(nums[maxIndex]);//左root.left = Construct(nums,leftIndex,maxIndex-1);root.right=Construct(nums,maxIndex+1,rightIndex);return root;}
}

617.合并二叉树：同时处理两个二叉树，在一个二叉树上操作，前序遍历。
700.二叉搜索树中的搜索：自己忽略了二叉搜索树是个有序树。
98.验证二叉搜索树：自己写代码碰到了陷阱，题目要求的是所有左子树的节点而不是只比较该节点的左节点。
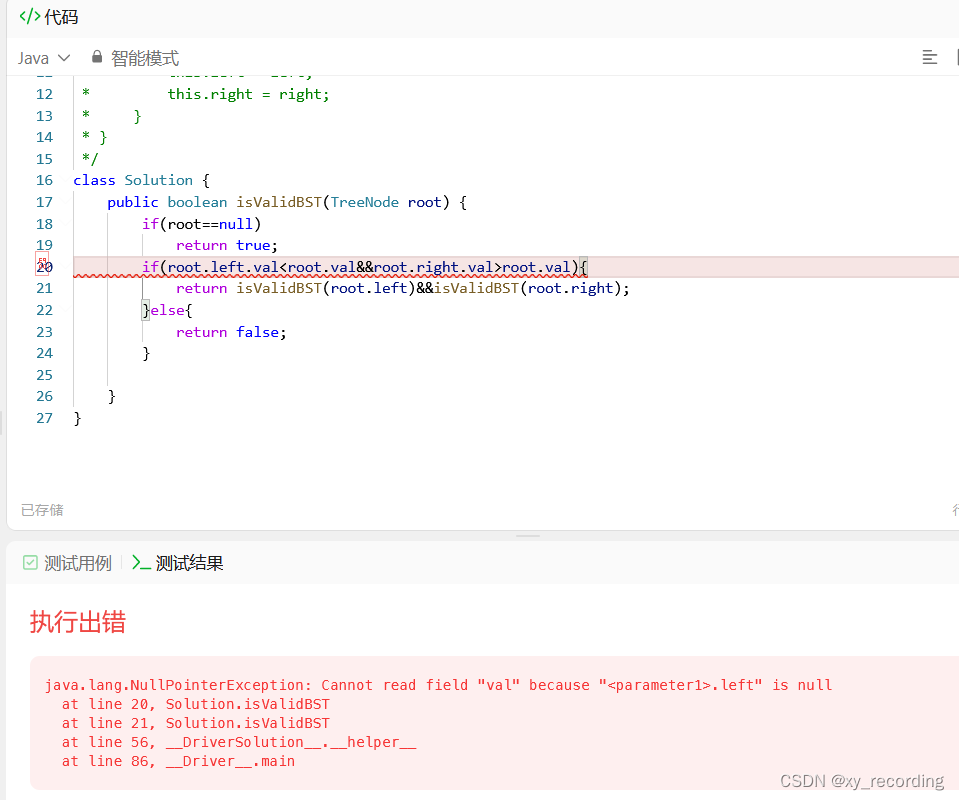增加了判断左右节点不为空的情况之后还是会无法通过全部测试样例：
这样写会因为下面的情况而错误
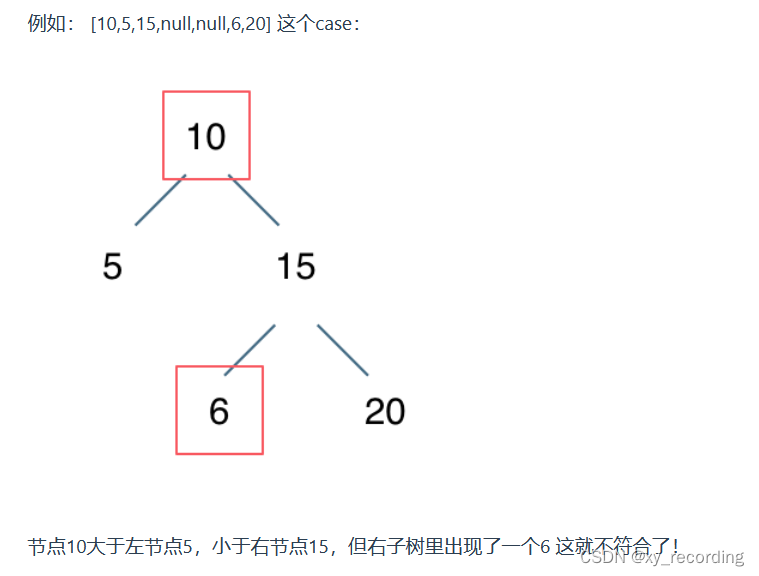这道题有思路是简单的，但是难点在于能否写出通过全部样例的代码。通常写的代码是递归每一个节点的左右子树的大小关系，而并不能表明左右子树的所有都是满足大小关系的。看了题解之后觉得，利用一步步更新的边界值来限定节点会规范这个问题。
这道题和700题有思想相近的地方，都是通过更新限定来递归。

自己实现过程中遇到哪些困难

654.最大二叉树：这道题有两种想法，第一种是更耗时耗空间的方法，也就是我上面写的看完随想录之后的想法，它耗时的原因是每次递归都重新创建数组，这个数组是根据找到最大值的索引下标后从原数组更新得来的，而每次的创建过程都会对时间和空间进行消耗。我在看了答案之后发现，每次可以在原数组上操作，递归函数输入参数为原数组nums和要构建子树的数组的左索引下标和右索引下标。自己写代码的过程中发现自己并不会更新索引下标，困在了左右子树不同索引下标的疑惑中，没有想清楚。问了同学之后明白了在每次递归函数的处理逻辑中，前序遍历的左子树和右子树的边界是变化的，左边是leftIndex到maxIndex-1，右边是maxIndex+1到rightIndex。这点还是需要好好理解一下的。

这篇关于代码随想录算法训练营第20天 |654.最大二叉树、 617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---