代码随想录算法训练营第三十二天|122.买卖股票的最佳时机II，55. 跳跃游戏，45.跳跃游戏II

本文主要是介绍代码随想录算法训练营第三十二天|122.买卖股票的最佳时机II，55. 跳跃游戏，45.跳跃游戏II，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

122.买卖股票的最佳时机II

题目链接：122.买卖股票的最佳时机II

文档讲解：代码随想录

视频讲解：贪心算法也能解决股票问题！LeetCode：122.买卖股票最佳时机II

思路

在低价的时候买入，在连续天数内的最高价时卖出。

假如第0天买入，第3天卖出，则利润为：price[3] - price[0].

相当于(price[3] - price[2]) + (price[2] - price[1]) + (price[1] - price[0]) .

如果此时利润最高，只需要每相邻两天之间的利润是正值，把所有正值相加即可。

代码

class Solution {
public:int maxProfit(vector<int> &prices) {int result = 0;for (int i = 1; i < prices.size(); i++) {if (prices[i] - prices[i - 1] > 0)result += prices[i] - prices[i - 1];}return result;}
};

55. 跳跃游戏

题目链接：55. 跳跃游戏

文档讲解：代码随想录

视频讲解：贪心算法，怎么跳跃不重要，关键在覆盖范围 | LeetCode：55.跳跃游戏

思路

不考虑每次跳几步，只考虑每次可以跳跃的最大步数，不断更新最大能够覆盖的范围，看最大范围能够到终点。

代码

class Solution {
public:bool canJump(vector<int> &nums) {int step = 0;for (int i = 0; i <= step; i++) {if (i + nums[i] > step) {step = i + nums[i];}if (step >= nums.size() - 1)return true;}return false;}
};

45.跳跃游戏II

题目链接：45.跳跃游戏II

文档讲解：代码随想录

视频讲解：贪心算法，最少跳几步还得看覆盖范围 | LeetCode： 45.跳跃游戏II

思路

每次都走最多的步，计算最大步数之内所有步数能够覆盖的最大范围，下一次走覆盖范围的最大步数。

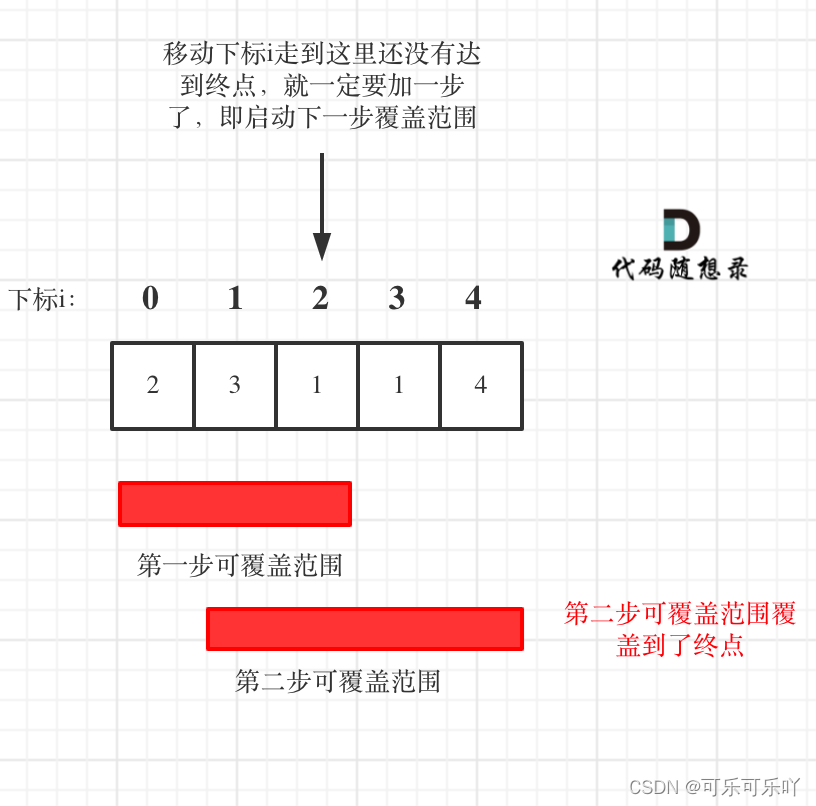
如上图，第一步最大跳两步能到达2的位置，那么在这两步之内的所有步数的下一次能够到达的最大范围是最大步数内所有步数的下一次能够覆盖距离的和，即1和2位置所能跳跃步数的和。在上图中，红色覆盖的范围内最多只需两步即可到达。

代码

class Solution {
public:int jump(vector<int> &nums) {if (nums.size() == 1)return 0;int curDistance = nums[0];int nextDistance = nums[0];int ans = 1;for (int i = 1; i < nums.size(); i++) {nextDistance = max(i + nums[i], nextDistance);if (curDistance >= nums.size() - 1)break;if (i == curDistance) {ans++;curDistance = nextDistance;}}return ans;}
};

这篇关于代码随想录算法训练营第三十二天|122.买卖股票的最佳时机II，55. 跳跃游戏，45.跳跃游戏II的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---