本文主要是介绍伸展树Splay,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Splay树,中文名一般叫做伸展树。和Treap树相同,作为平衡树,它也是通过左旋和右旋来调整树的结构。和Treap树不同的是,Splay树不再用一个随机的权值来进行平衡,而是用固定的调整方式来使得调整之后的树会比较平衡。
在左旋右旋的基础上,Splay树定义了3个操作:
1. Zig
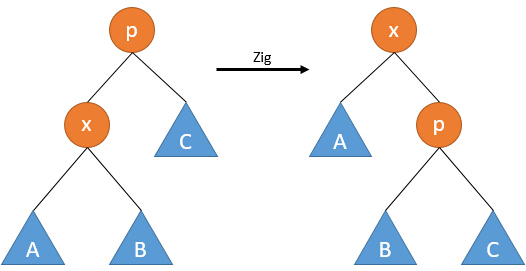
直接根据x节点的位置,进行左旋或右旋。
该操作将x节点提升了一层。
2. Zig-Zig
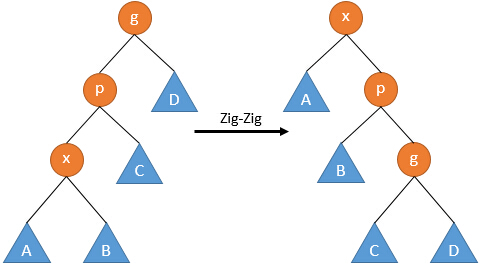
若p不是根节点,还有父亲节点g,且p和x同为左儿子或右儿子,则进行Zig-Zig操作:
当x,p同为左儿子时,依次将p和x右旋;
当x,p同为右儿子时,依次将p和x左旋。
注意此处不是将x连续Zig两次。该操作将x节点提升了两层。
3. Zig-Zag
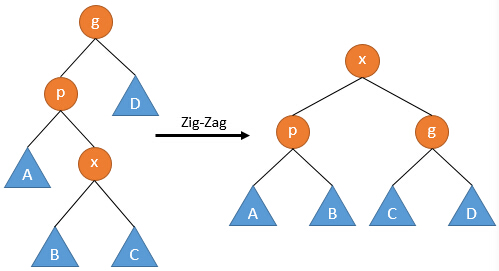
若p不是根节点,则p还有父亲节点g。且p和x不同为左儿子或右儿子,则进行Zig-Zag操作:
当p为左儿子,x为右儿子时,将x节点先左旋再右旋;
当p为右儿子,x为左儿子时,将x节点先右旋再左旋。
该操作将x节点提升了两层。
进一步在Zig,Zig-Zig和Zig-Zag操作上,Splay树定义了"Splay"操作。
对于x以及x的祖先y,splay(x, y),表示对x节点进行调整,使得x是y的儿子节点,需要保证y节点一定是x节点祖先。
值得一提的是,大多数情况下我们希望通过splay操作将x旋转至整棵树的根节点。此时只需令y=NULL即可实现。
(1)Splay树的插入和查询操作和普通的二叉搜索树没有什么大的区别,需要注意的是每次插入和查询结束后,需要对访问节点做一次Splay操作,将其旋转至根。
(2)同时由于Splay的特性,我们还有两个特殊的查询操作。在树中查找指定数key的前一个数和后一个数。
我们先将key旋转至根,那么key的前一个数一定是根节点左儿子的最右子孙,同时key的后一个数一定是根节点右儿子的最左子孙。
(3)删除操作:
首先我们查找到key的前一个数prev和后一个数next。将prev旋转至根,再将next旋转为prev的儿子。此时key节点一定是next的左儿子。那么直接将next的左儿子节点删去即可。
这里你可能会担心如果key是数中最小或者是最大的数怎么办?
一个简单的处理方式是手动加入一个超级大和超级小的值作为头尾。
(4)要删除[a,b],那么我就要想办法把[a,b]的数旋转到一个子树上,再将这个子树删掉就行了。
方法和删除一个数相同,我首先将a的前一个数prev和b的后一个数next找出来。
同样将prev旋转至根,再将next旋转为prev的儿子。
那么此时next的左子树一定就是所有[a,b]之间的数了!
如果a,b不在树中呢?把a,b插入树中,做完之后再删除不就好了!
输入
第1行:1个正整数n,表示操作数量,100≤n≤200,000
第2..n+1行:可能包含下面3种规则:
1个字母'I',紧接着1个数字k,表示插入一个数字k到树中,1≤k≤1,000,000,000,保证每个k都不相同
1个字母'Q',紧接着1个数字k。表示询问树中不超过k的最大数字
1个字母'D',紧接着2个数字a,b,表示删除树中在区间[a,b]的数。
输出
若干行:每行1个整数,表示针对询问的回答,保证一定有合法的解
6 I 1 I 2 I 3 Q 4 D 2 2 Q 2
3 1
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <ctime>#define MIN_K 0
#define MAX_K 1000000001using namespace std;//伸展树Splay
struct node
{node(int k){father = left = right = NULL;key = k;}int key;node *father, *left, *right;
}*root;//与平衡树中节点不同
void left_rotate(node* a)
{node* b = a->father;a->father = b->father;if (b->father == NULL){root = a;}else{if (b->father->left == b)b->father->left = a;elseb->father->right = a;}b->right = a->left;if(a->left)a->left->father = b;a->left = b;b->father = a;
}void right_rotate(node* a)
{node* b = a->father;a->father = b->father;if (b->father == NULL){root = a;}else{if (b->father->left == b)b->father->left = a;elseb->father->right = a;}b->left = a->right;if(a->right)a->right->father = b;a->right = b;b->father = a;
}void zig(node* a)
{if (a->father->left == a)right_rotate(a);elseleft_rotate(a);
}void zig_zig(node* a)
{if (a->father != root){if (a->father->left == a && a->father->father->left == a->father){right_rotate(a->father);right_rotate(a);}else if (a->father->right == a && a->father->father->right == a->father){left_rotate(a->father);left_rotate(a);}}
}void zig_zag(node* a)
{if (a->father != root){if (a->father->right == a && a->father->father->left == a->father){left_rotate(a);right_rotate(a);}else if (a->father->left == a && a->father->father->right == a->father){right_rotate(a);left_rotate(a);}}
}//表示对x节点进行调整,使得x是y的孩子节点,需保证y为x的祖先
//若希望通过splay操作将x旋转至整棵树的根节点。只需令y=NULL即可
void splay(node* x, node* y)
{if (x == NULL)return;while (x->father != y){node* p = x->father;if (p->father == y){if(x != root)zig(x);}else{if (x != root)zig_zig(x);if (x != root)//需要判断一下zig_zag(x);}}
}//需要注意的是每次插入和查询结束后,需要对访问节点做一次Splay操作,将其旋转至根
node* bst_find(node* n, int key)
{if (key == n->key) return n;else if (key < n->key){if (n->left == NULL)return NULL;elsereturn bst_find(n->left, key);}else if (key > n->key){if (n->right == NULL)return NULL;elsereturn bst_find(n->right, key);}
}void find(int key)
{node* n = bst_find(root, key);splay(n, NULL);
}node* bst_insert(node* n, int key)
{if (key < n->key){if (n->left == NULL){n->left = new node(key);n->left->father = n;return n->left;}elsereturn bst_insert(n->left, key);}else{if (n->right == NULL){n->right = new node(key);n->right->father = n;return n->right;}elsereturn bst_insert(n->right, key);}
}void insert(int key)
{if (root == NULL)root = new node(key);else{node* n = bst_insert(root, key);splay(n, NULL);}
}node* findPre(int key)
{find(key);node* n = root->left;while (n->right)n = n->right;return n;
}node* findNext(int key)
{find(key);node* n = root->right;while (n->left)n = n->left;return n;
}void deleteByKey(int key)
{node* pre = findPre(key);node* next = findNext(key);splay(pre, NULL);splay(next, pre);if(next)next->left = NULL;
}void deleteByAB(int a, int b)
{if (a <= MIN_K) a = MIN_K + 1;if (b >= MAX_K) b = MAX_K - 1;if (bst_find(root, a) == NULL)insert(a);node* pre = findPre(a);if (bst_find(root, b) == NULL)insert(b);node* next = findNext(b);splay(pre, NULL);splay(next, pre);if (next)next->left = NULL;
}int ans = 0;
int Q(node* n, int key)
{if (key == n->key)return key;if (key < n->key){if (n->left == NULL)return ans;elsereturn Q(n->left, key);}else{if (n->right == NULL)return n->key;else{ans = n->key;return Q(n->right, key);}}
}int main()
{int n, a, b;char c;insert(MIN_K);insert(MAX_K);cin >> n;while (n--){cin >> c >> a;if (c == 'I'){insert(a);}else if (c == 'Q'){int ans = Q(root, a);cout << (ans == 0?a:ans) << endl;}else if (c == 'D'){cin >> b;deleteByAB(a, b);}}return 0;
}
输入
第1行:1个正整数n,表示操作数量,100≤n≤200,000
第2..n+1行:可能包含下面3种规则:
1个字母'I',紧接着1个数字k,表示插入一个数字k到树中,1≤k≤1,000,000,000,保证每个k都不相同
1个字母'Q',紧接着1个数字k。表示询问树中不超过k的最大数字
1个字母'D',紧接着2个数字a,b,表示删除树中在区间[a,b]的数。
输出
若干行:每行1个整数,表示针对询问的回答,保证一定有合法的解
6 I 1 I 2 I 3 Q 4 D 2 2 Q 2
3 1
这篇关于伸展树Splay的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



