本文主要是介绍隐马尔可夫模型(HMM)硬啃西瓜书,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
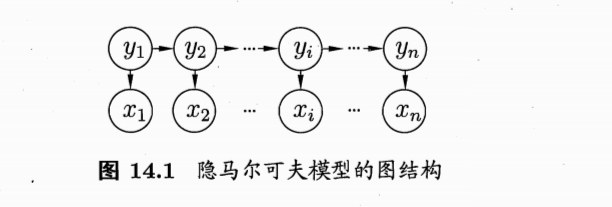
隐马尔可夫模型(HMM)
好吧隐马尔可夫模型出现的次数实在有点多;今天来讲讲吧
先来四个概念:
- 可见状态链 观测结果
- 隐含状态链 产生结果的实体类型
- 转换概率 相邻实体之间转换的概率
- 输出概率 实体输出结果的概率
两个基本假设:
1) 齐次马尔科夫链假设。即任意时刻的隐藏状态只依赖于它前一个隐藏状态。
2) 观测独立性假设;实体输出结果的概率完全独立
本来说的是参考几篇文章来写,tmd好多错啊;没办法只能自己去啃书了

提问:
- R 一般在实例中指什么?
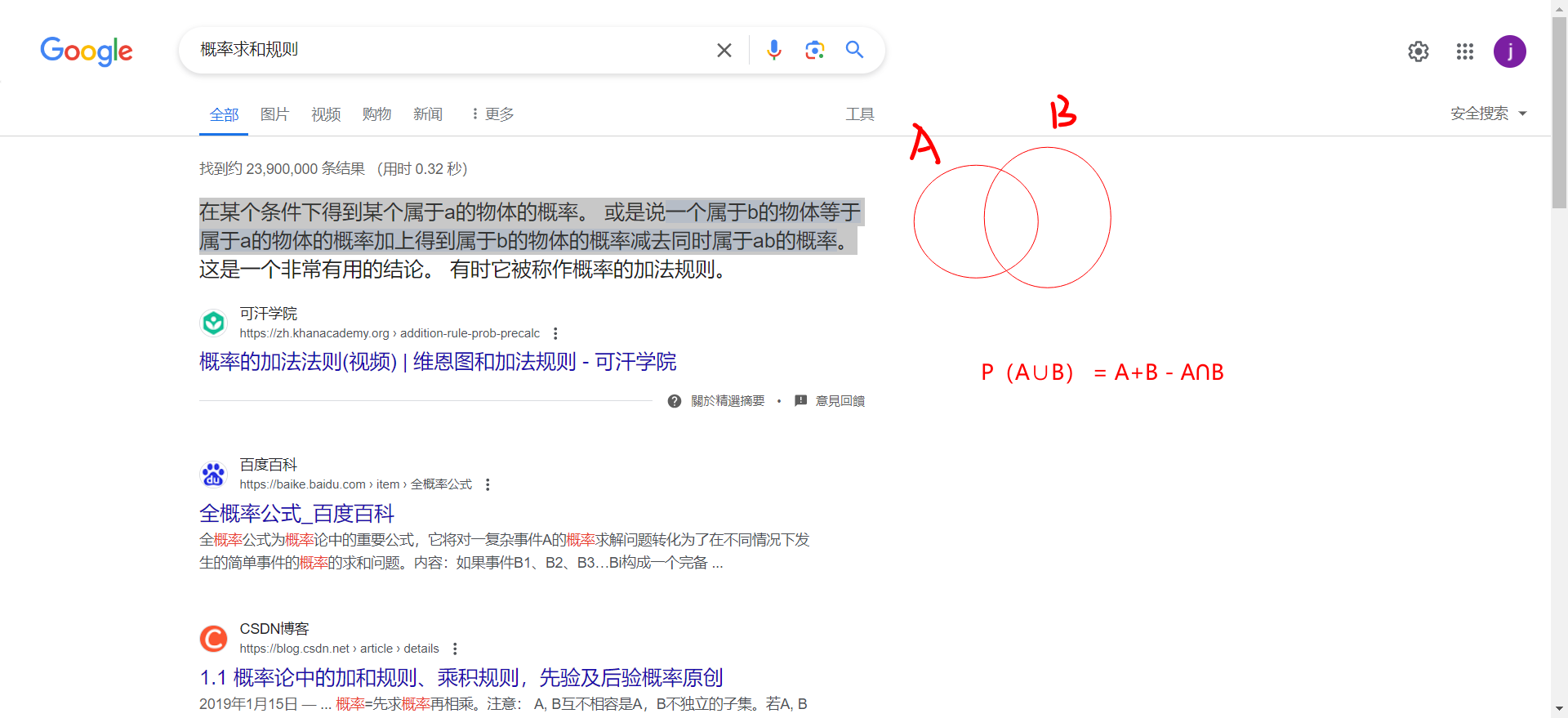
- 什么是概率求和规则?
- 如何利用概率求和规则消去R?

关于复杂度的说明 ⬆👆
在某个条件下得到某个属于a的物体的概率。 或是说一个属于b的物体等于属于a的物体的概率加上得到属于b的物体的概率减去同时属于ab的概率。
暂时回答不了剩下的两个,先姑且理解为 不用我们HMM模型你就很难求出来就好~
HMM
一种动态贝叶斯网;我知道我知道你肯定一堆破问题(为啥动态,啥就是贝叶斯网了,别急等等我告你)

这三种概率弄到你的脑子里;
然后三个基本问题:

我个人觉得第三个问题最有意思,因为特别像我们平时说的极大似然估计


好好好 势函数的概念真尼玛抽象–> 可以简单理解为一种考虑了相邻团的依赖的团的概率分布,然后后面那个Z 就是归一化,保证了这些势函数(自己定义出来的抽象玩意儿)之间的和等于1;后面团的概念和离散数学里的一个玩意儿挺像的;多读两遍吧应该是能读懂的,小伙子加油;
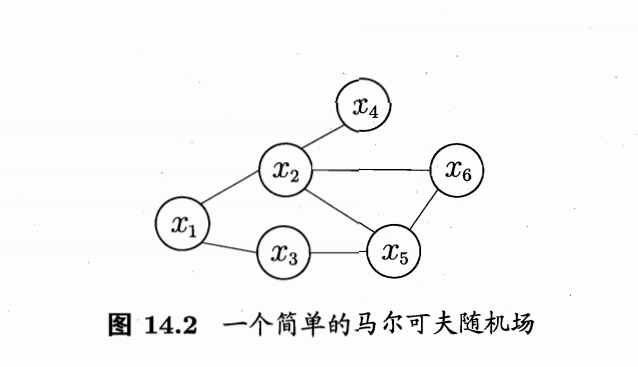

好理解的;看上面
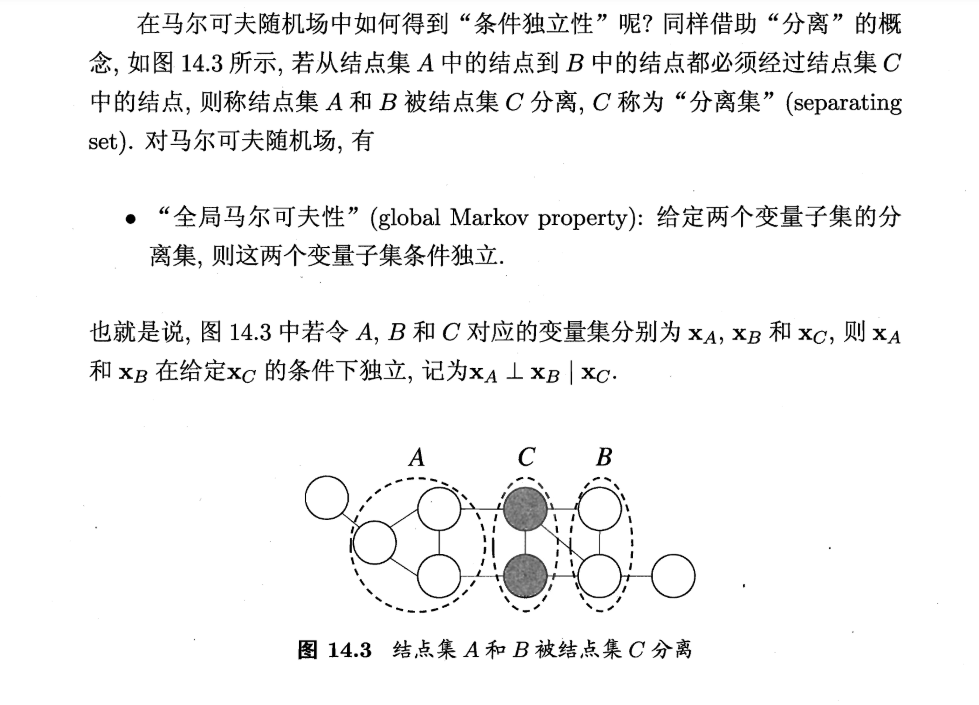
多bb一嘴,会的当我放屁;条件独立:有了某个条件A就B独立(原来独不独立不知道哈,也不关心)另外,这玩意儿读起来是真的爽啊!比那些水了吧唧的博客爽多了

令人遗憾的是这里卡死了又一次;复习了一下概率论里面的全概率公式,这里又打通了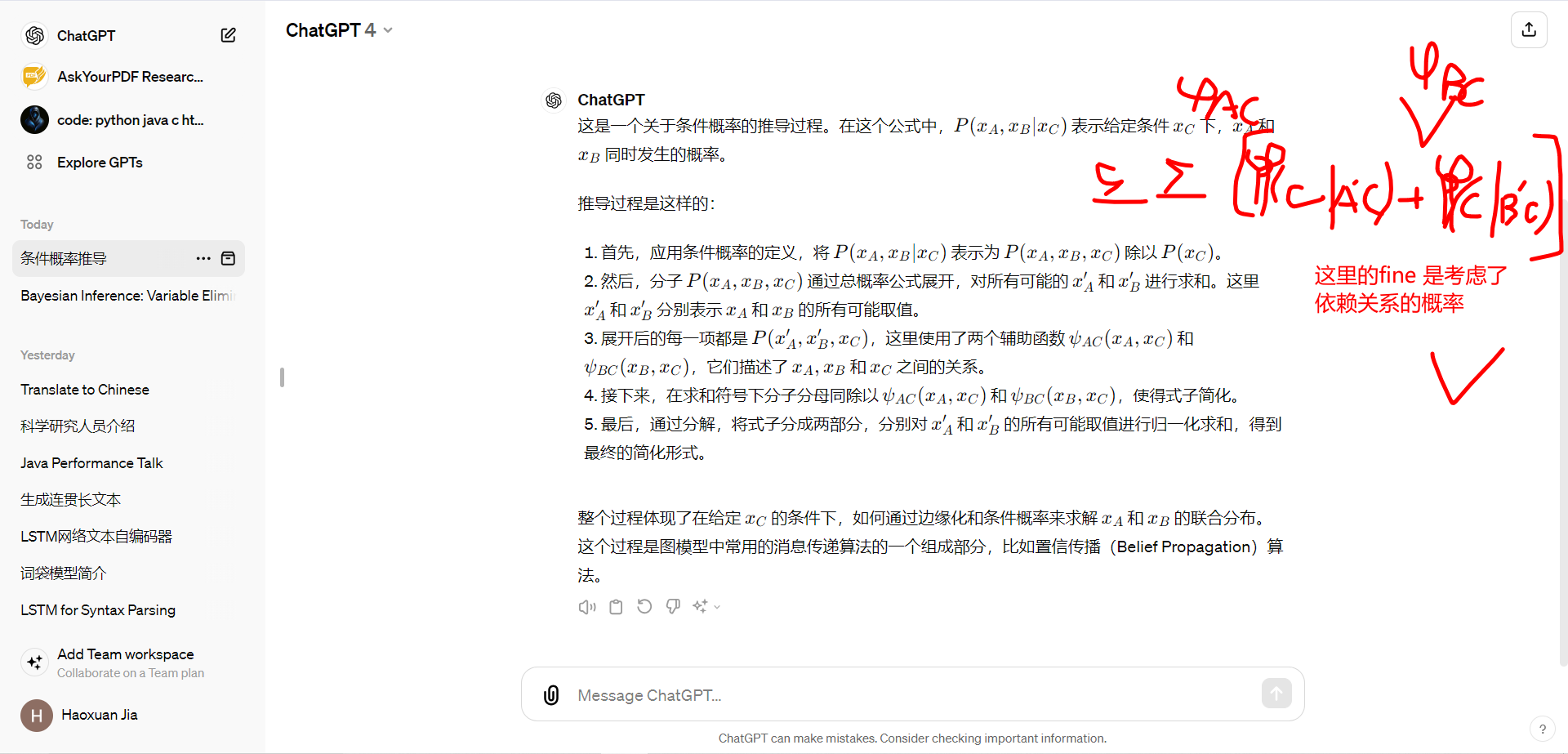
(上面那个应该是*号 因为fine的定义就是这张关联的依赖)如果我们尝试把A’∪B’当作样本空间的一个划分的话确实会得到上面的式子;but A∪B 并非啊;(MD 我学的 好烦躁啊)


截至到条件随机场之前,理论上差不多可以自圆其说了,但是我相信还是会有很多bug 后续迭代吧……
学习方法总述:
- 极大似然估计 – 面对不熟悉的理论问题,尽可能往自己熟悉的相关domain 迁移,在一开始 的过程中忽略看似矛盾的地方,后续随着内容和理解的深入迭代,会得到更好的特征
- 反向传播 – 对于一些复杂的推理来说 ,结果往往是比较简单的,可以又果溯因,结合正向传播会更快的得到推导的理解
- 学习时候大多数时间要觉得自己是傻逼,别人是牛逼;努力去弄明白他要讲什么东西,他想告诉你的是什么,忽略他讲的一些不如意的地方,反而去理解,沉淀;有基础以后,创新的时候要自己反馈,认为自己是牛逼,别人都是傻逼;
-----参考《机器学习(周志华)》
这篇关于隐马尔可夫模型(HMM)硬啃西瓜书的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!