本文主要是介绍开源代码分享(21)-两阶段鲁棒优化的主动配电网动态无功优化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.引言
由于分布式电源接入配电网的比例不断升高,分布式电源出力和负荷难以准确预测,给配电网的无功优化带来了许多不确定性,使得传统的的确定性无功优化模型得到的控制策略不准确。考虑设备损耗,配电网的无功控制装置中的分组投切电容器组和有载调压分接头,这些装置不能频繁的操作,虽然这些装置能够有效的应对电压波动,但是针对快速的秒级到分钟级的较小电压波动
的,一方面受限于操作次数的限制,不能频繁的去操作;另一方面离散装置响应速度比较慢,无法有效应对电压波动。针对负荷和分布式电源的预测曲线,由于预测的误差较大,得出的控制策略可能导致电压可能越界,所以在制定控制策略的时候必须考虑不确定性。
输电网中由于线路电阻 R 通常小于线路电抗 X,输电网中有功和无功通常能够解耦控制,而配电网 R/X 的比值较大,无法实现有功与无功的解耦控制,所以配电网的电压控制需要有功与无功协调控制。主动配电网中含储能和可控DG,这些装置能够快速地进行控制,如何协调快速设备和慢速设备(CB)的控制来应对主动配电网中的不确定性是一个值得深入研究的课题。
2. 鲁棒优化模型及求解方法
鲁棒优化是用于解决不确性问题的一种方法,不同于随机规划对于不确定量假设满足某种不确定参数的分布,突破了过多依靠先验知识的服从概率分布的假定 [71] 。鲁棒优化的目的是:求的解满足所有约束条件,对于可能出现的所有情况,在最坏的情况下使得目标函数值最优的解。
2.1 鲁棒优化一般模型
鲁棒优化模型一般如下所示:
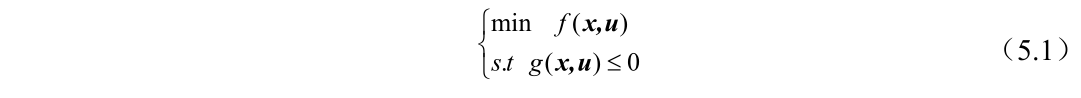
式中:x为决策变量;u为不确定参数; f(x,u)为目标函数; g(x,u)≤0为约束条件。u为不确定参数,根据不确定参数所在的集合不同,可以分为:盒式不确定集、椭球不确定集、多面体不确定集[72]。
上述鲁棒优化模型中通常难以求解需要进行等价转化,其基本思路,是将不确定参数以集合和的形式加入到鲁棒模型中,这样以数学的形式从而将鲁棒模型的不确定量剔除掉,转化为鲁棒等价模型,通常使用soyster 提出的min-max模型,又称之为单阶段鲁棒模型,其形式如下:

2.2 两阶段鲁棒优化简介

2.3两阶段鲁棒优化模型求解方法
两阶段鲁棒优化求解方法有:列约束生成法[73] ( column-and-con-straingeneration,C&CG)和 Benders分解法,C&CG算法的求解性能要优于Bender分解法。
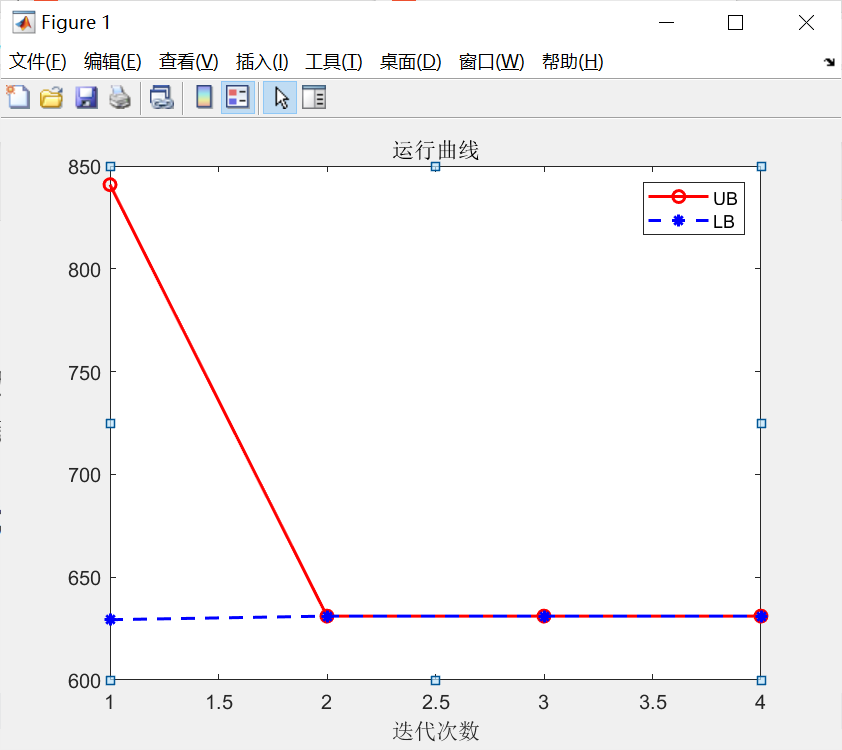
C&CG算法的求解是分为主问题和子问题来求解,主问题为目标函数确定的一个下界值,首先假设不确定场景为离散的形式,U= {u1,…,ur},这样对应的决策变量为{x1 , …,xr},由于不确定场景不是全部的场景,这样优化结果为目标函数的一个下界值,所枚举出的不确定场景与优化结果无关,这是因为子问题求解出的场景不断的添加到主问题中,使主问题中目标函数的下界值不断增大,通常而言,如果不确定场景占有的全部场景比较多,那么收敛速度会加快,其主问题模型如下:
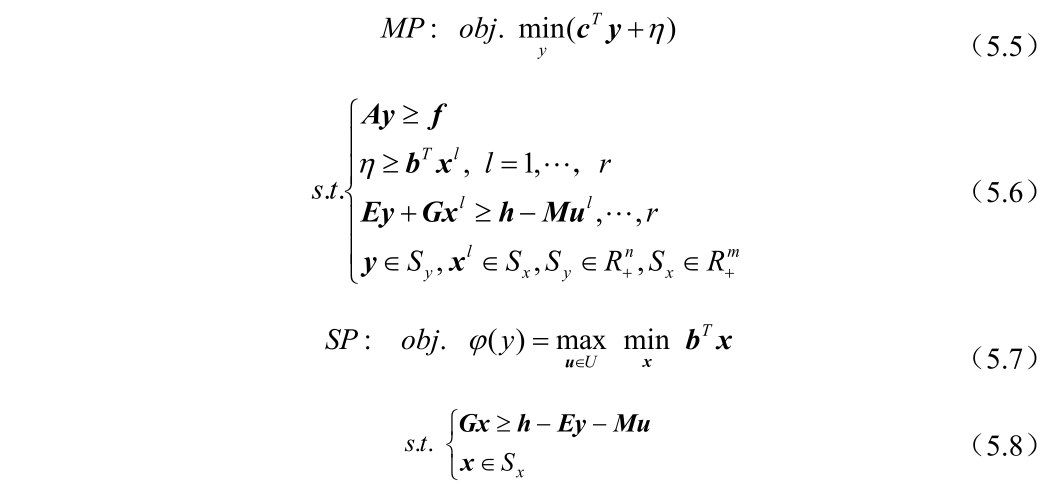
主问题得到的决策变量 y 带到子问题中来,会得到不确定场景 u 和决策变量 x,由于得到的场景是主问题中决策变量所对应的场景,那么子问题得到的值是目标函数的一个上界值,那么再将子问题中的场景加到主问题中,主问题的决策变量又可以得到目标函数的一个下界值,反复上一过程,直到上界值和确定值之差满足于收敛判据,此时迭代结束。
3.两阶段鲁棒优化的电压控制模型
为了应对分布式电源和负荷的不确定性对配电网运行决策带来的影响,建立了两阶段的鲁棒优化模型,将离散变量作为第一阶段的控制变量,如储能的充放电标志的二进制变量,分组投切电容器组的投切组数,将连续变量作为第二阶段的控制变量,如储能的充放电功率,静止无功补偿器的补偿量。一方面由于含有离散控制变量的装置启动时间较长,启动周期为数十分钟到几个小时,
另一方面含有离散控制变量装置频繁操作会降低设备的使用寿命,控制策略是连续变量的装置,相对于含离散变量的装置的来说,其能够快速地进行控制,所以离算变量的控制策略在应对配电网的不确定性制定的控制策略中会显得尤其重要,从而将其作为第一阶段的控制变量,使得在第一阶段离散装置的控制策略,能够保证配电网在最恶劣的场景下,第二阶段的控制策略使得配电网安全、稳定、经济地运行。建立的两阶段鲁棒优化的模型主动管理装置中含有储能、分组投切电容器组、静止无功补偿器,DG,详细解释在第二章和第三章中介绍过了,其模型如下:
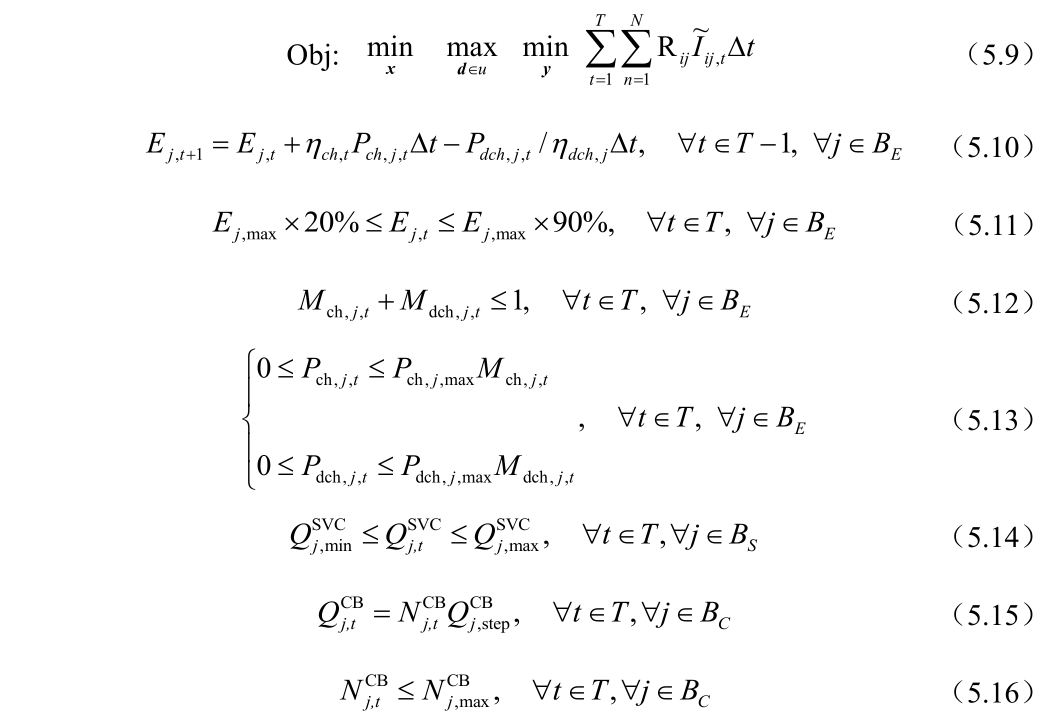
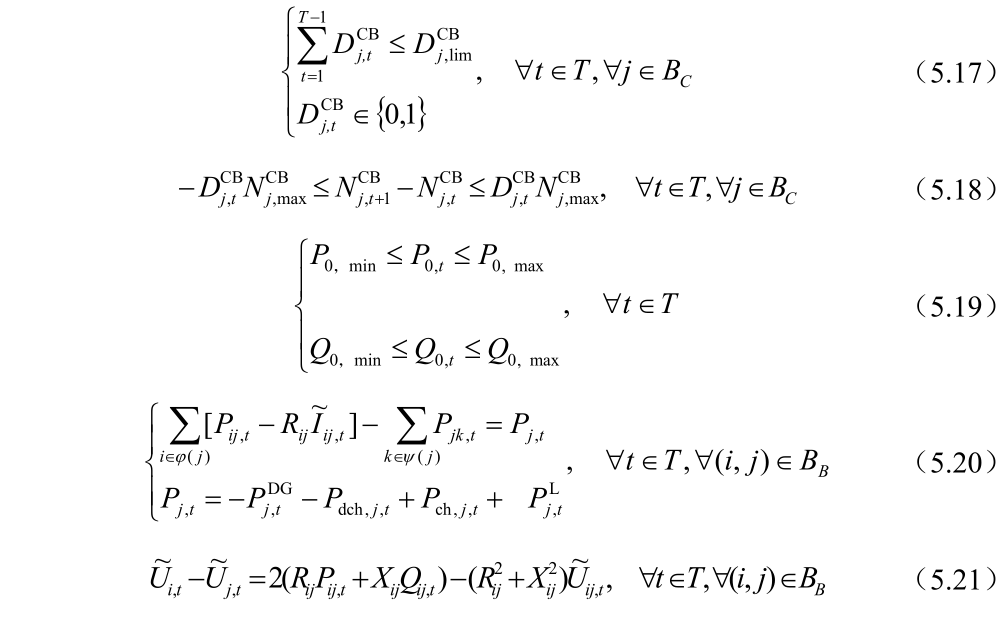
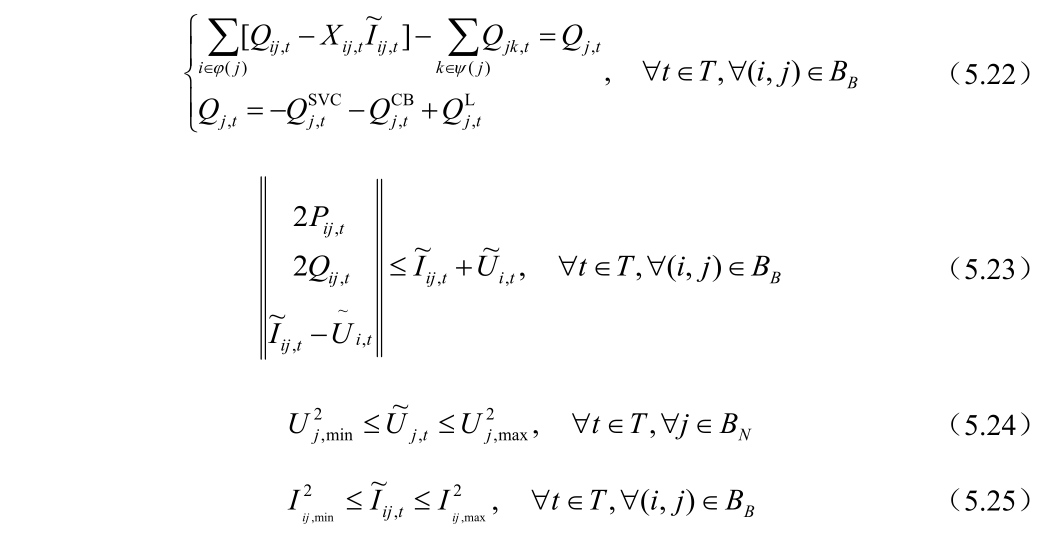
为了表述方便,将式(5.9)~(5.25)用紧凑型的表达式如下:

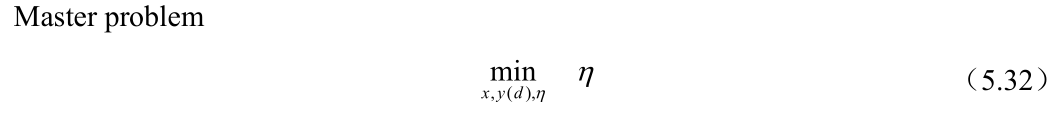
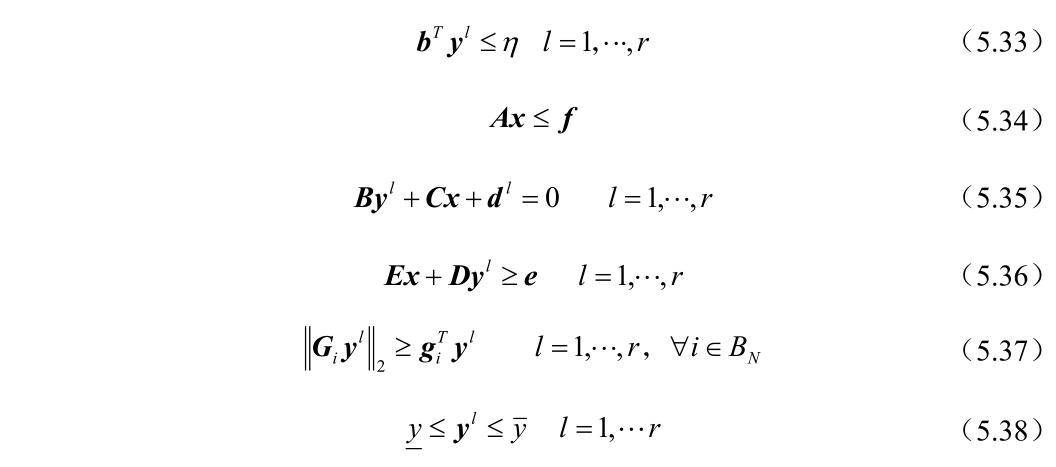
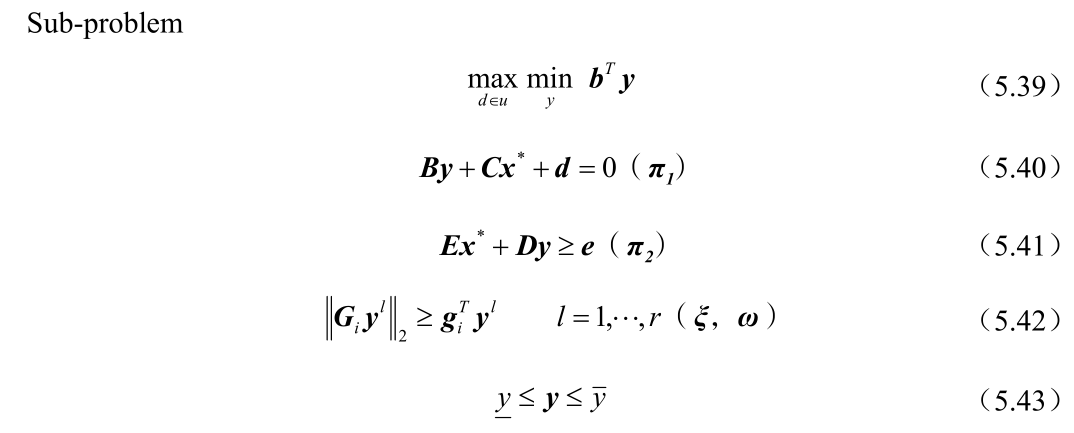







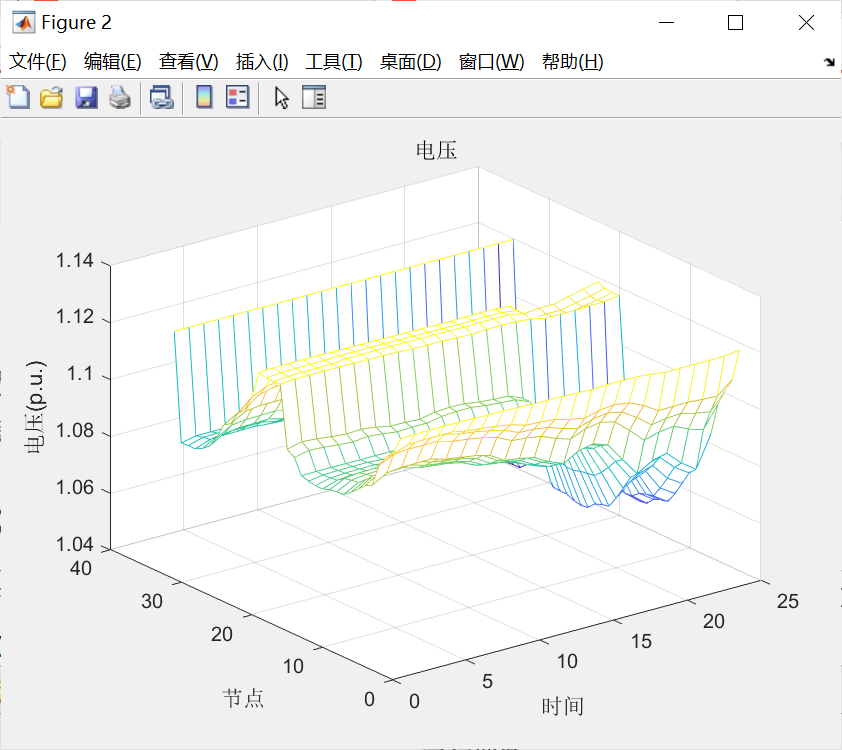
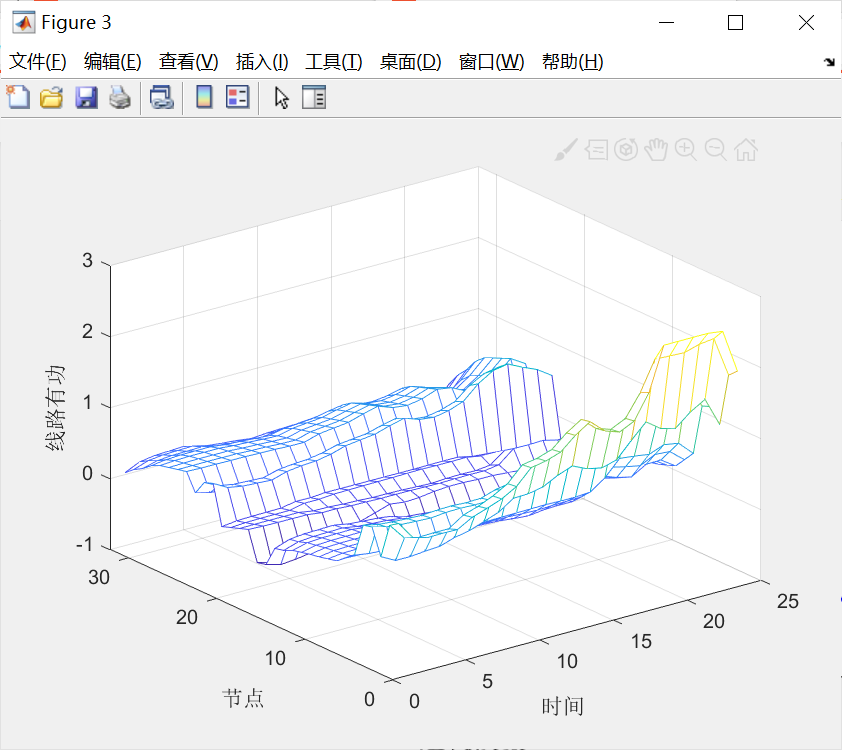
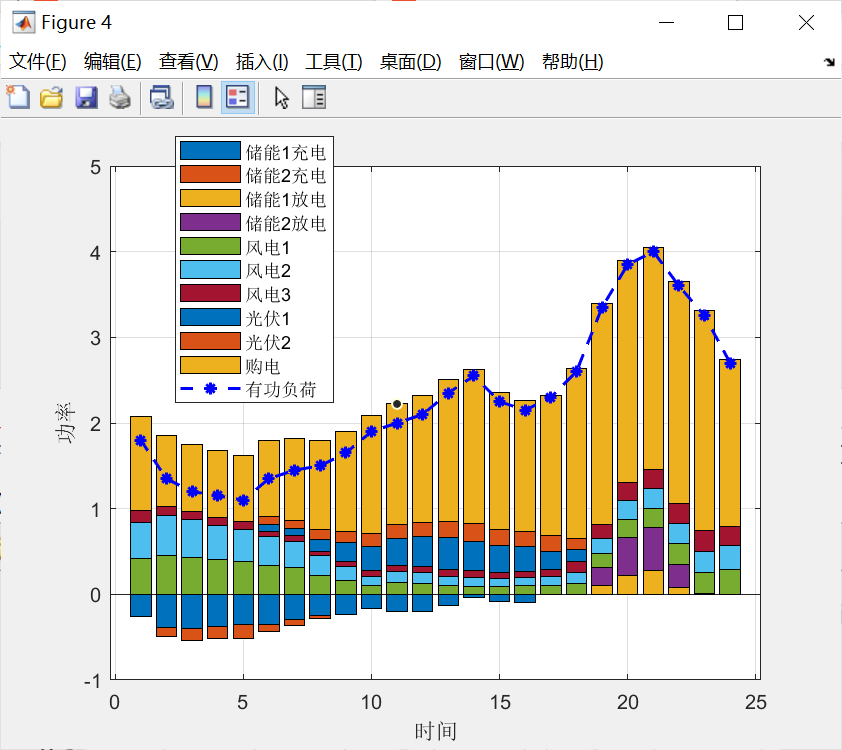
4.代码运行结果
5.完整代码获取
两阶段鲁棒优化的主动配电网动态无功优化的matlab代码资源-CSDN文库
这篇关于开源代码分享(21)-两阶段鲁棒优化的主动配电网动态无功优化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




