模拟退火（ACdreamer）

2024-04-16 03:38
文章标签 模拟退火 acdreamer

本文主要是介绍模拟退火（ACdreamer），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

转自大佬https://blog.csdn.net/ACdreamers/article/details/10019849
周日的中南多校考了道最小包含多边形的退火题，那就向yddalao学习，学学退火。

模拟退火算法是用来求解最优化问题的算法。比如著名的TSP问题，函数最大值最小值问题等等。接下来将以如下几个方面来详细介绍模拟退火算法。

Contents

  1. 模拟退火算法认识

  2. 模拟退火算法描述

  3. 费马点问题求解

  4. 最小包含球问题求解

  5. 函数最值问题求解

  6. TSP问题求解

  7. 模拟退火算法认识

    爬山算法也是一个用来求解最优化问题的算法，每次都向着当前上升最快的方向往上爬，但是初始化不同可能

    会得到不同的局部最优值，模拟退火算法就可能跳出这种局部最优解的限制。模拟退火算法是模拟热力学系统

    中的退火过程。在退火过程中是将目标函数作为能量函数。大致过程如下

    初始高温 => 温度缓慢下降=> 终止在低温 （这时能量函数达到最小，目标函数最小）

    在热力学中的退火过程大致是变温物体缓慢降温而达到分子之间能量最低的状态。设热力学系统S中有有限个且

    离散的n个状态，状态的能量为，在温度下，经过一段时间达到热平衡，这时处于状态的概率为

    模拟退火算法也是贪心算法，但是在其过程中引入了随机因素，以一定的概率接受一个比当前解要差的解，并且

    这个概率随着时间的推移而逐渐降低。

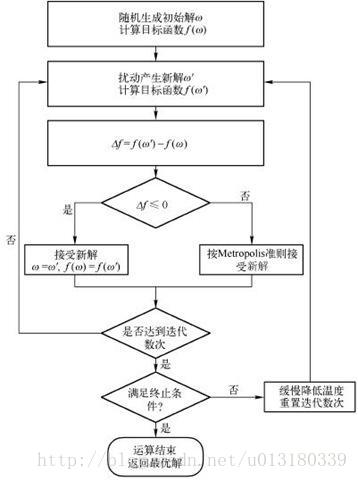
  8. 模拟退火算法描述

    若，即移动后得到更优的解，那么总是接受改移动。

    若，即移动后得到更差的解，则以一定的概率接受该移动，并且这个概率随时间推移

    逐渐降低。这个概率表示为

    由于是退火过程，所以dE < 0，这个公式说明了温度越高出现一次能量差为dE的降温概率就越大，温度越低，

    出现降温的概率就越小，由于dE总是小于0，所以P(dE)取值在0到1之间。伪码如下

  9. 费马点问题求解

    题目：http://poj.org/problem?id=2420

    题意：给n个点，找出一个点，使这个点到其他所有点的距离之和最小，也就是求费马点。

代码：

    #include <iostream>#include <string.h>#include <stdlib.h>#include <stdio.h>#include <time.h>#include <math.h>#define N 1005#define eps 1e-8     //搜索停止条件阀值#define INF 1e99     #define delta 0.98   //温度下降速度#define T 100        //初始温度using namespace std;int dx[4] = {0, 0, -1, 1};int dy[4] = {-1, 1, 0, 0};  //上下左右四个方向struct Point{double x, y;};Point p[N];double dist(Point A, Point B){return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));}double GetSum(Point p[], int n, Point t){double ans = 0;while(n--)ans += dist(p[n], t);return ans;}//其实我觉得这玩意儿根本不叫模拟退火double Search(Point p[], int n){Point s = p[0];    //随机初始化一个点开始搜索double t = T;      //初始化温度double ans = INF;  //初始答案值while(t > eps){bool flag = 1;while(flag){flag = 0;for(int i = 0; i < 4; i++)    //上下左右四个方向{Point z;z.x = s.x + dx[i] * t;z.y = s.y + dy[i] * t;double tp = GetSum(p, n, z);if(ans > tp){ans = tp;s = z;flag = 1;}}}t *= delta;}return ans;}int main(){int n;while(scanf("%d", &n) != EOF){for(int i = 0; i < n; i++)scanf("%lf %lf", &p[i].x, &p[i].y);printf("%.0lf\n", Search(p, n));}return 0;}

题目：平面上给定n条线段，找出一个点，使这个点到这n条线段的距离和最小。

代码：

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <math.h>#define N 1005
#define eps 1e-8     //搜索停止条件阀值
#define INF 1e99     
#define delta 0.98   //温度下降速度
#define T 100        //初始温度using namespace std;int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};  //上下左右四个方向struct Point
{double x, y;
};Point s[N], t[N];double cross(Point A, Point B, Point C)  
{  return (B.x - A.x) * (C.y - A.y) - (B.y - A.y) * (C.x - A.x);  
}  double multi(Point A, Point B, Point C)  
{  return (B.x - A.x) * (C.x - A.x) + (B.y - A.y) * (C.y - A.y);  
}  double dist(Point A, Point B)
{return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}double GetDist(Point A, Point B, Point C)  
{  if(dist(A, B) < eps) return dist(B, C);  if(multi(A, B, C) < -eps) return dist(A, C);  if(multi(B, A, C) < -eps) return dist(B, C);  return fabs(cross(A, B, C) / dist(A, B));  
}  double GetSum(Point s[], Point t[], int n, Point o)
{double ans = 0;while(n--)ans += GetDist(s[n], t[n], o);return ans;
}double Search(Point s[], Point t[], int n, Point &o)
{o = s[0];    double tem = T;      double ans = INF;while(tem > eps){bool flag = 1;while(flag){flag = 0;for(int i = 0; i < 4; i++)    //上下左右四个方向{Point z;z.x = o.x + dx[i] * tem;z.y = o.y + dy[i] * tem;double tp = GetSum(s, t, n, z);if(ans > tp){ans = tp;o = z;flag = 1;}}}tem *= delta;}return ans;
}int main()
{int n;while(scanf("%d", &n) != EOF){for(int i = 0; i < n; i++)scanf("%lf %lf %lf %lf", &s[i].x, &s[i].y, &t[i].x, &t[i].y);Point o;double ans = Search(s, t, n, o);printf("%.1lf %.1lf %.1lf\n", o.x, o.y, ans);  }return 0;
}

  1. 最小包含球问题求解

    题目：http://poj.org/problem?id=2069

    题意：给定三维空间的n点，找出一个半径最小的球把这些点全部包围住。

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>#define N 55
#define eps 1e-7
#define T 100
#define delta 0.98
#define INF 1e99using namespace std;struct Point
{double x, y, z;
};Point p[N];double dist(Point A, Point B)
{return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y) + (A.z - B.z) * (A.z - B.z));
}double Search(Point p[], int n)
{Point s = p[0];double t = T;double ans = INF;while(t > eps){int k = 0;for(int i = 0; i < n; i++)if(dist(s, p[i]) > dist(s, p[k]))k = i;double d = dist(s, p[k]);ans = min(ans, d);s.x += (p[k].x - s.x) / d * t;s.y += (p[k].y - s.y) / d * t;s.z += (p[k].z - s.z) / d * t;t *= delta;}return ans;
}int main()
{int n;while(cin >> n && n){for(int i = 0; i < n; i++)cin >> p[i].x >> p[i].y >> p[i].z;double ans = Search(p, n);printf("%.5lf\n", ans);}return 0;
}

  1. 函数最值问题求解

    题目：http://acm.hdu.edu.cn/showproblem.php?pid=2899

    题意：给出方程，其中，输入，求的最小值。

    分析：本题可以用经典的二分法求解，这种方法比较简单，就不说了。主要来说模拟退火做法。

代码：

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
#include <stdio.h>
#include <time.h>
#include <math.h>#define ITERS 10
#define T 100
#define eps 1e-8
#define delta 0.98
#define INF 1e99using namespace std;double x[ITERS];int Judge(double x, double y)
{if(fabs(x - y) < eps) return 0;return x < y ? -1 : 1;
}double Random()
{double x = rand() * 1.0 / RAND_MAX;if(rand() & 1) x *= -1;return x;
}double F(double x, double y)
{return 6 * x * x * x * x * x * x * x + 8 * x * x * x * x * x * x + 7 * x * x * x + 5 * x * x - y * x;
}void Init()
{for(int i = 0; i < ITERS; i++)x[i] = fabs(Random()) * 100;
}double SA(double y)
{double ans = INF;double t = T;while(t > eps){for(int i = 0; i < ITERS; i++){double tmp = F(x[i], y);for(int j = 0; j < ITERS; j++){double _x = x[i] + Random() * t;if(Judge(_x, 0) >= 0 && Judge(_x, 100) <= 0){double f = F(_x, y);if(tmp > f) x[i] = _x;}} }t *= delta;}for(int i = 0; i < ITERS; i++)ans = min(ans, F(x[i], y));return ans;
}int main()
{int t;scanf("%d", &t);while(t--){double y;scanf("%lf", &y);srand(time(NULL));Init();printf("%.4lf\n", SA(y));}return 0;
}

  1. TSP问题求解

    TSP问题是一个NP问题，但是可以求近似解，通过模拟退火算法实现，代码如下

代码：

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
#include <stdio.h>
#include <time.h>
#include <math.h>#define N     30      //城市数量
#define T     3000    //初始温度
#define EPS   1e-8    //终止温度
#define DELTA 0.98    //温度衰减率
#define LIMIT 10000   //概率选择上限
#define OLOOP 1000    //外循环次数
#define ILOOP 15000   //内循环次数using namespace std;//定义路线结构体
struct Path
{int citys[N];double len;
};//定义城市点坐标
struct Point
{double x, y;
};Path path;        //记录最优路径
Point p[N];       //每个城市的坐标
double w[N][N];   //两两城市之间路径长度
int nCase;        //测试次数double dist(Point A, Point B)
{return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}void GetDist(Point p[], int n)
{for(int i = 0; i < n; i++)for(int j = i + 1; j < n; j++)w[i][j] = w[j][i] = dist(p[i], p[j]);
}void Input(Point p[], int &n)
{scanf("%d", &n);for(int i = 0; i < n; i++)scanf("%lf %lf", &p[i].x, &p[i].y);
}void Init(int n)
{nCase = 0;path.len = 0;for(int i = 0; i < n; i++){path.citys[i] = i;if(i != n - 1){printf("%d--->", i);path.len += w[i][i + 1];}elseprintf("%d\n", i);}printf("\nInit path length is : %.3lf\n", path.len);
}void Print(Path t, int n)
{printf("Path is : ");for(int i = 0; i < n; i++){if(i != n - 1)printf("%d-->", t.citys[i]);else printf("%d\n", t.citys[i]);}printf("\nThe path length is : %.3lf\n", t.len);
}Path GetNext(Path p, int n)
{Path ans = p;int x = (int)(n * (rand() / (RAND_MAX + 1.0)));int y = (int)(n * (rand() / (RAND_MAX + 1.0)));while(x == y){x = (int)(n * (rand() / (RAND_MAX + 1.0)));y = (int)(n * (rand() / (RAND_MAX + 1.0)));}swap(ans.citys[x], ans.citys[y]);ans.len = 0;for(int i = 0; i < n - 1; i++)ans.len += w[ans.citys[i]][ans.citys[i + 1]];cout << "nCase = " << nCase << endl;Print(ans, n);nCase++;return ans;
}void SA(int n)
{double t = T;srand(time(NULL));Path curPath = path;Path newPath = path;int P_L = 0;int P_F = 0;while(1)       //外循环，主要更新参数t，模拟退火过程{for(int i = 0; i < ILOOP; i++)    //内循环，寻找在一定温度下的最优值{newPath = GetNext(curPath, n);double dE = newPath.len - curPath.len;if(dE < 0)   //如果找到更优值，直接更新{curPath = newPath;P_L = 0;P_F = 0;}else{double rd = rand() / (RAND_MAX + 1.0);    if(exp(dE / t) > rd && exp(dE / t) < 1)   //如果找到比当前更差的解，以一定概率接受该解，并且这个概率会越来越小curPath = newPath;P_L++;}if(P_L > LIMIT){P_F++;break;}}if(curPath.len < newPath.len)path = curPath;if(P_F > OLOOP || t < EPS)break;t *= DELTA;}
}int main()
{freopen("TSP.data", "r", stdin);int n;Input(p, n);GetDist(p, n);Init(n);SA(n);Print(path, n);printf("Total test times is : %d\n", nCase);return 0;
}

数据：TSP.data

27
41 94
37 84
53 67
25 62
7 64
2 99
68 58
71 44
54 62
83 69
64 60
18 54
22 60
83 46
91 38
25 38
24 42
58 69
71 71
74 78
87 76
18 40
13 40
82 7
62 32
58 35
45 21

https://blog.csdn.net/ACdreamers/article/details/10019849

这篇关于模拟退火（ACdreamer）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/907711。

相关文章

模拟退火判断一个圆是否可以放在一个多边形内

模拟退火判断一个圆是否可以放在一个多边形内

/*给定n个点的一个多边形，一个圆的半径，判断圆是否可以放在多边形里*//* ***********************************************Author :rabbitCreated Time :2014/7/3 22:46:38File Name :2.cpp**********************************************
阅读更多...
模拟退火求n个点到某点距离和最短

模拟退火求n个点到某点距离和最短

/*找出一个点使得这个店到n个点的最长距离最短，即求最小覆盖圆的半径用一个点往各个方向扩展，如果结果更优，则继续以当前步长扩展，否则缩小步长*/#include<stdio.h>#include<math.h>#include<string.h>const double pi = acos(-1.0);struct point {double x,y;}p[1010];int
阅读更多...
基于SA模拟退火算法的多车辆TSP问题求解matlab仿真

基于SA模拟退火算法的多车辆TSP问题求解matlab仿真

目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述        基于SA模拟退火算法的多车辆TSP问题求解matlab仿真，三个车辆分别搜索其对应的最短路径，仿真后得到路线规划图和SA收敛曲线。 2.测试软件版本以及运行结果展示 MATLAB2022A版本运行 （完整程序运行后无水印）
阅读更多...
SA（模拟退火）优化算法MATLAB源码详细中文注解

SA（模拟退火）优化算法MATLAB源码详细中文注解

以优化SVM算法的参数c和g为例，对SA（模拟退火）算法MATLAB源码进行了逐行中文注解。 完整程序和示例文件地址：http://download.csdn.net/detail/u013337691/9644107 链接：http://pan.baidu.com/s/1i5G0gPB 密码：4ge8 % 使用模拟退火法寻优SVM中的参数c和g% 使用METROPOLIS接受准则%%
阅读更多...
模拟退火TSP问题

模拟退火TSP问题

模拟退火算法在求解最优值问题上有很大的优势，前面一篇博文介绍了用模拟退火算法实现求函数的最大、最小值问题。本文主要介绍如何用python实现模拟退火在TSP（旅行商）问题中的应用，源代码请移步pySA。网络上有不少文章介绍模拟退火TSP应用，可以对比着看。我们对实现的算法进行了测试，动态可视化更加形象。 1. TSP 问题描述 这个问题实际上就是求解最小路劲的问题，不过目前pySA实现还
阅读更多...
模拟退火算法求函数最大、小值——python实现

模拟退火算法求函数最大、小值——python实现

模拟退火算法（Simulate Anneal，SA）是一种通用概率演算法，用来在一个大的搜寻空间内找寻命题的最优解。模拟退火是由S.Kirkpatrick, C.D.Gelatt和M.P.Vecchi在1983年所发明的。V.Černý在1985年也独立发明此演算法。模拟退火算法是解决TSP问题的有效方法之一。 模拟退火的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退
阅读更多...
数学建模赛前备赛——模拟退火算法

数学建模赛前备赛——模拟退火算法

一.什么是智能优化算法 智能优化算法本质上是一个优化算法,它通过不断优化模型的参数,使得系统表现达到最优，常见的只能优化算法有很多，比如说蚁群算法,遗传算法以及我们今天的主角——模拟退火算法。 二.模拟算法的前身——爬山算法 爬山算法是一种简单的优化算法，它每次会从当前解的临近解空间中选取一个最优解来作为当前解，直到达到一个局部最优解,但是爬山算法有一个致命的缺陷，就是容易陷入局部最优解，无
阅读更多...
模拟退火算法解多元函数

模拟退火算法解多元函数

模拟退火算法解多元函数 题目： F ( x ) = 11.16386 − 0.0903 x 1 − 0.1487 x 2 − 0.0664 x 3 + 0.09074 x 4 − 2.452 ∗ 1 0 − 4 x 1 x 2 + 6.228 ∗ 1 0 − 5 x 1 x 3 + 2.457 ∗ 1 0 − 3 x 1 x 4 + 3.8688 ∗ 1 0 − 3 x 2 x 3 − 6.4
阅读更多...
模拟退火算法分析

模拟退火算法分析

一. 爬山算法 ( Hill Climbing )          介绍模拟退火前，先介绍爬山算法。爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。          爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。如图1所示：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索
阅读更多...
模拟退火算法--自己做的ppt

模拟退火算法--自己做的ppt

原文地址：模拟退火算法--自己做的ppt 作者：雪后DE阳光 1、  模拟退火算法（起源） 模拟退火算法起源于物理退火。 􀂄物理退火过程： （1）       加温过程 （2）       等温过程 （3）       冷却过程                                      物理退火原理 􀂄1953年，Metropolis提出重要性采样法，即以概率
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2