Python实现时间序列ARIMA模型（附带超详细理论知识和完整代码实现）

本文主要是介绍Python实现时间序列ARIMA模型（附带超详细理论知识和完整代码实现），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0 结果

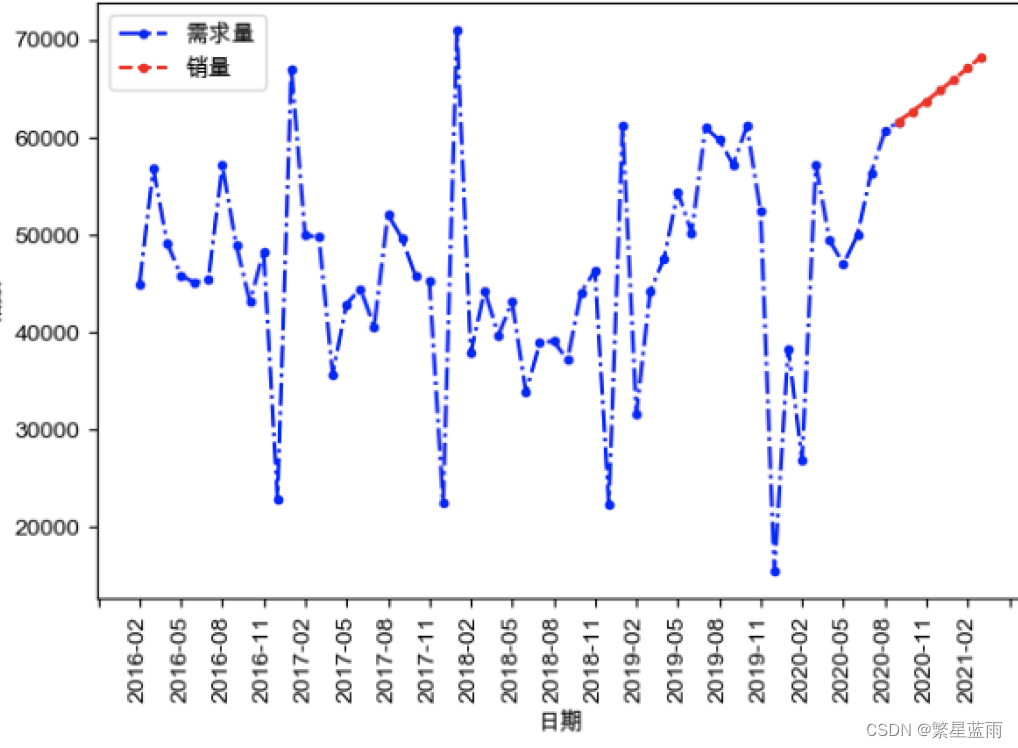
1 介绍

时间序列分析的基本思想：寻找系统的当前值与其过去的运行记录（观察数据）的关系，建立能够比较精确地反映时间序列中动态依存关系的数学模型，并借此对系统的未来行为进行预报。

ARIMA模型（Autoregressive Integrated Moving Average model,差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动）)，是时间序列预测分析方法之一。ARIMA(p，d，q)中，AR是“自回归”，p为自回归项数；MA为“滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

该模型十分简单，只需要带有时间的变量，但是
1.要求时序数据是稳定的（stationary），或者是通过差分化(differencing)后是稳定的。
2.本质上只能捕捉线性关系，而不能捕捉非线性关系。

注意⚠️：采用ARIMA模型预测时序数据，必须是稳定的，如果不稳定的数据，是无法捕捉到规律的。比如股票数据用ARIMA无法预测的原因就是股票数据是非稳定的，常常受政策和新闻的影响而波动。

2 建模

2.1 预备知识

2.1.1 ADF检验结果（单位根检验统计量）

ADF检验结果作用：

• 1，ADF检验是一种检验时间序列是否平稳的方法，其原假设是存在单位根，即非平稳。根据ADF检验的结果，可以通过比较检验统计量和临界值，以及p值和显著性水平，来判断是否拒绝原假设。
• 2，如果拒绝原假设，可以认为数据是平稳的；如果不拒绝原假设，可以认为数据是非平稳的，需要进行差分后再检验
• 3，另外，还需要根据不同的模型，判断数据是趋势平稳、截距平稳还是不含截距和时间趋势的平稳。

ADF检验结果的五个参数含义：

• 第一个参数：adt检验的结果，简称为T值，表示t统计量。

• 第二个参数：简称为p值，表示t统计量对应的概率值。p值表示在原假设（零假设）的条件下，样本发生或观测值出现的概率。若p值小于小概率事件的阈值（0.05或0.01），那么拒绝原假设（即数据是平稳的），否则接受原假设。

  • 若P<0.01，说明是较强的判定结果，拒绝假定的参数取值；若0.01<P<0.05，说明较弱的判定结果，拒绝假定的参数取值；若P>0.05，说明结果更倾向于接受假定的参数取值。

• 第三个参数：滞后阶数，时间序列中的滞后阶数指的是当前数据点与前面的几个数据点之间的时间间隔数量。

  • 如果滞后阶数选择得太低，那么模型可能无法捕捉时间序列的所有重要特征，导致预测精度不够高；
  • 如果滞后阶数选择得太高，那么模型就会过于复杂，过度拟合训练数据，从而无法泛化到新的数据上。

• 第四个参数：AIC(赤池信息量准则)衡量统计模型拟合优良性的一种标准,选取AIC最小的模型。

  • 它建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。
  • 模型选择是在模型复杂度与模型对数据集描述能力（即似然函数）之间寻求最佳平衡。
  • 很多参数估计问题均采用似然函数作为目标函数，当训练数据足够多时，可以不断提高模型精度，但提高了模型复杂度，同时带来过拟合的问题。

• 配合第一个参数一起看的，是在99%，95%，90%置信区间下的临界的ADF检验值。

下面为程序示例返回的ADF检验结果：

原始序列的ADF检验结果为： (
-1.065623530928928, 
0.7285844104901973, 
11, 
43, 
{'1%': -3.5925042342183704, '5%': -2.931549768951162, '10%': -2.60406594375338}, 922.2003862834713)

观察角度:

• 1，由第二个参数可得p值为0.7285844104901973，无法拒绝原假设，即数据不稳定。
• 2，由第一个参数可得T值为-1.065623530928928，由第五个参数结合第一个参数可得-1.065623530928928大于'10%': -2.60406594375338，即接受原假设，数据不稳定。

2.1.2 差分序列的白噪声检验（这里使用Ljung-Box检验）

作用：白噪声序列有个特点，任意两项的协方差/相关性系数都是零，也就是说任意不同的两项之间不存在相关性关系。 如果一个时间序列是白噪声，那么就不具有分析的意义，因为从一个纯随机的东西中找不出任何有价值的规律。

参数说明：

• lbvalue：测试的统计量
• pvalue：基于卡方分布的p统计量
  • 如果pvalue值大于0.05，就说明我们无法拒绝原假设（该序列是白噪声序列），这个时间序列的确就是白噪声序列。

示例：

差分序列的白噪声检验结果为：      lb_stat     lb_pvalue
1  33.952495  5.647422e-09

这里得到的p值为5.647422e-09，即拒绝原假设，序列不是白噪声。

2.1.3 ARIMA模型（差分整合移动平均自回归模型）的三个参数:p，d，q

p：代表预测模型中采用的时序数据本身的滞后数(lags) ,也叫做AR/Auto-Regressive项
d：代表时序数据需要进行几阶差分化，才是稳定的，也叫Integrated项。
q：代表预测模型中采用的预测误差的滞后数(lags)，也叫做MA/Moving Average项

ARIMA模型的特例：
1，ARIMA(0,1,0) ：（此时当d=1，p和q为0时，称为random walk模型，）该模型表示每一个时刻的位置，只与上一时刻的位置有关。
2，ARIMA(1,0,0) ，（此时p=1, d=0,q=0，称为 first-order autoregressive model）该模型说明时序数据是稳定的和自相关的。
3，ARIMA(1,1,0)，（此时p=1,d=1,q=0，称为differenced first-order autoregressive model） ，该模型说明时序数据在一阶差分化之后是稳定的和自回归的，即一个时刻的差分（y）只与上一个时刻的差分有关。
4，ARIMA(0,1,1) ,(此时p=0, d=1 ,q=1，称为simple exponential smoothing with growth模型)=该模型说明数据在一阶差分后是稳定的和移动平均的，即一个时刻的估计值的差分与上一个时刻的预测误差有关。

2.1.4 自相关和偏自相关（用于识别ARMA模型）

1，作用：自相关和偏自相关用于测量当前序列值和过去序列值之间的相关性，并指示预测将来值时最有用的过去序列值。

2，区别自相关函数和偏自相关函数

• 自相关函数 (ACF)：延迟为 k 时，这是相距 k 个时间间隔的序列值之间的相关性。
• 偏自相关函数 (PACF)：延迟为 k 时，这是相距 k 个时间间隔的序列值之间的相关性，同时考虑了间隔之间的值。

3，自相关图和偏自相关图：

• 自相关图：有助于判断时间序列数据是否存在季节性或周期性变化，并且可以用来选择合适的时间序列模型。如果一个时间序列数据存在季节性变化，则其自相关图通常会呈现出明显的周期性模式。
• 偏自相关图：可以帮助我们确定时间序列数据中的短期相关性，从而选择合适的时间序列模型。如果一个时间序列数据存在短期相关性，则其偏自相关图通常会显示出急速衰减的模式。

4，区别：截尾和拖尾

• 截尾：在大于某个常数k后快速趋于0为k阶截尾
• 拖尾：始终有非零取值，不会在k大于某个常数后就恒等于零(或在0附近随机波动)

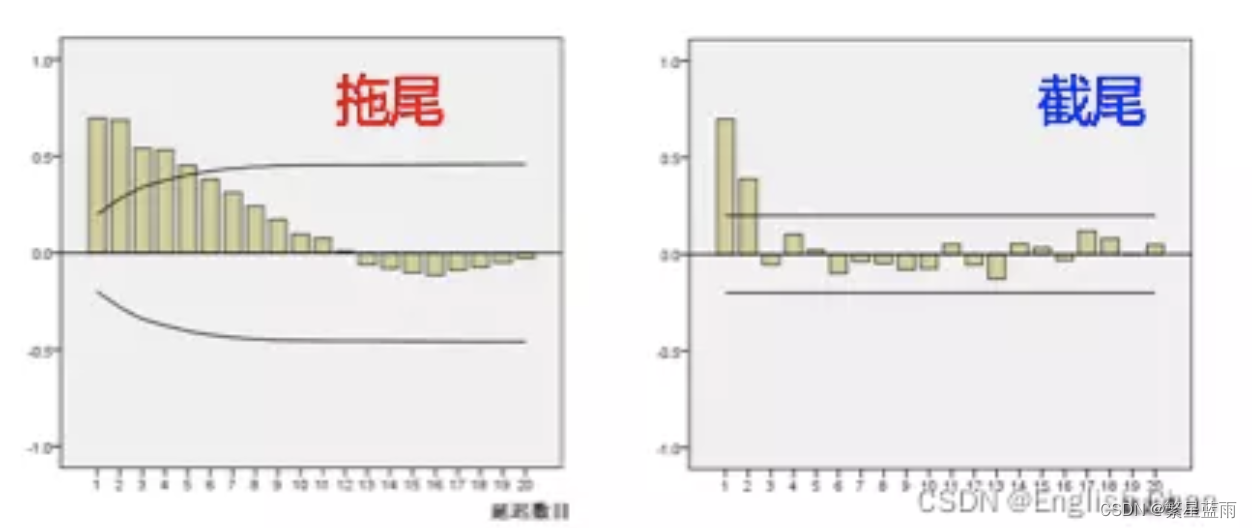
观察自相关图和偏自相关图，然后根据如下表选择模型：

2.1.5 AIC与BIC（用于确定p，q参数）

贝叶斯信息准则（Bayesian Information Criterion，BIC）：与AIC相似，用于模型选择BIC的惩罚项比AIC的大，考虑了样本数量，样本数量过多时，可有效防止模型精度过高造成的模型复杂度过高。

区别：

• 1，AIC=2k−2ln(L)，BIC=kln(n)−2ln(L)。
• 2，当n ≥ 10²时，kln(n)≥2k，所以BIC相比AIC在大数据量时对模型参数惩罚得更多，导致BIC更倾向于选择参数少的简单模型。

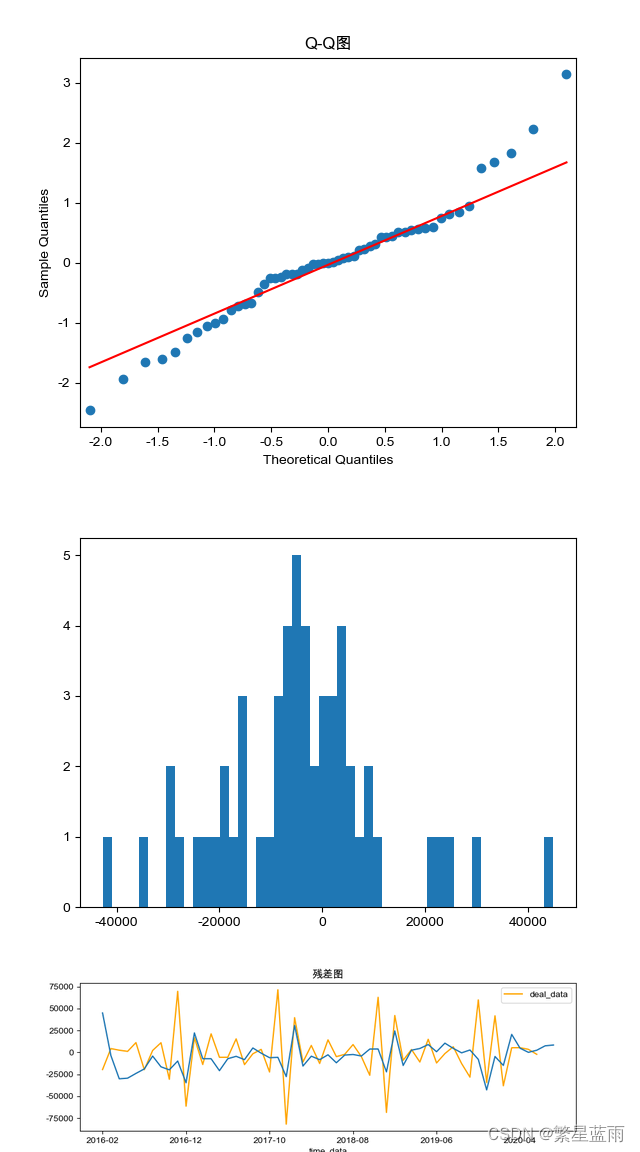
2.1.6 模型检验（残差检验， QQ图，Jarque-Bera检验，D-W检验）

• 残差检验：如果残差（残差 = 实际观测值 – 模型预测值）是正态分布，我们就可以认为他是随机的，如果它是随机的就可以认为它是对随机误差比较好的拟合；
• QQ图：检验残差是否满足正态分布；
• Jarque-Bera检验（雅克-贝拉检验）： 判断数据是否符合总体正态分布；
  • P值<指定水平0.05,拒绝原假设，认为样本数据在5%的显著水平下不服从正态分布；
  • 适用于 样本数量大于30 ，而且样本数越多，JB检验效果越准确。
• 利用D-W检验（残差序列自相关）：检验残差的自相关性；
  • 一般DW值在2附近（比如1.7-2.3之间），则说明没有自相关性，模型构建良好；

例子：

------------残差检验-----------
NormaltestResult(statistic=4.4959826117374515, pvalue=0.10561115214326909)------------Jarque-Bera检验-----------
Jarque-Bera test:
JB: 4.0642468241648775
p-value: 0.13105693759455012
Skew: 0.33412880151714236
Kurtosis: 4.151920700073933------DW检验:残差序列自相关----
1.71022123825392

2.2 建模详细过程

1）对数据绘图，进行 ADF 检验，观察序列是否平稳（一般为不平稳）；对于非平稳时间序列要先进行d阶差分运算，化为平稳时间序列；
2）对平稳时间序列进行白噪声检验，如果不是白噪声序列，则继续下面的建模；
3）使用AIC和BIC准则定阶q和p的值；

• 或者是p 值可从偏自相关系数（PACF）图的最大滞后点来大致判断，q 值可从自相关系数（ACF）图的最大滞后点来大致判断，得到最佳的阶数 p 和阶数 q；
• 或者是使用BIC矩阵来计算q和p的值；
  4）由以上得到的d、q、p得到ARIMA模型；
  5）最后对进行模型检验，例如残差检验，D-W检验（残差序列自相关）。

3 模型代码实现

3.1 详细步骤

1，引入头文件

from __future__ import annotations
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf #ACF与PACF
from statsmodels.tsa.arima.model import ARIMA #ARIMA模型
from statsmodels.graphics.api import qqplot  #qq图
from scipy import stats

2，把原始数据转为pandas.core.frame.DataFrame的数据进行操作，

• 直接从字典转换：

# dict类型的原始数据
need_data = {'2016-02': 44964.03, '2016-03': 56825.51, '2016-04': 49161.98, '2016-05': 45859.35, '2016-06': 45098.56, '2016-07': 45522.17, '2016-08': 57133.18, '2016-09': 49037.29, '2016-10': 43157.36, '2016-11': 48333.17, '2016-12': 22900.94,'2017-01': 67057.29, '2017-02': 49985.29, '2017-03': 49771.47, '2017-04': 35757.0, '2017-05': 42914.27, '2017-06': 44507.03, '2017-07': 40596.51, '2017-08': 52111.75, '2017-09': 49711.18, '2017-10': 45766.09, '2017-11': 45273.82, '2017-12': 22469.57,'2018-01': 71032.23, '2018-02': 37874.38, '2018-03': 44312.24, '2018-04': 39742.02, '2018-05': 43118.38, '2018-06': 33859.69, '201807': 38910.89, '2018-08': 39138.42, '2018-09': 37175.03, '2018-10': 44159.96, '2018-11': 46321.72, '2018-12': 22410.88,'2019-01': 61241.94, '2019-02': 31698.6, '2019-03': 44170.62, '2019-04': 47627.13, '2019-05': 54407.37, '2019-06': 50231.68, '2019-07': 61010.29, '2019-08': 59782.19, '2019-09': 57245.15, '2019-10': 61162.55, '2019-11': 52398.25, '2019-12': 15482.64,'2020-01': 38383.97, '2020-02': 26943.55, '2020-03': 57200.32, '2020-04': 49449.95, '2020-05': 47009.84, '2020-06': 49946.25, '2020-07': 56383.23, '2020-08': 60651.07}
# 转换为Dataframedata = {'time_data': list(need_data.keys()), 'click_value_rate': list(need_data.values())}df = pd.DataFrame(data)df.set_index(['time_data'], inplace=True) # 设置索引data = df

• 从excel中数据转换：

path = '/Users/mac/Downloads/时间序列模型测试数据.xlsx'
df=pd.read_excel(path)
# 更改列名
df.rename(columns={'data':'deal_data', 'time':'time_data'}, inplace = True)
# 设置索引
df.set_index(['time_data'], inplace=True)data = df

3， 对原始数据进行绘图；

    # 绘制时序图plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] # 用来正常显示中文标签# plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号# 绘图data.plot()# 图片展示plt.show()# 绘制自相关图plot_acf(data).show()# 绘制偏自相关图plot_pacf(data).show()
平稳性检测print(u'原始序列的ADF检验结果为：', ADF(data[u'deal_data']))

下图为时序图：

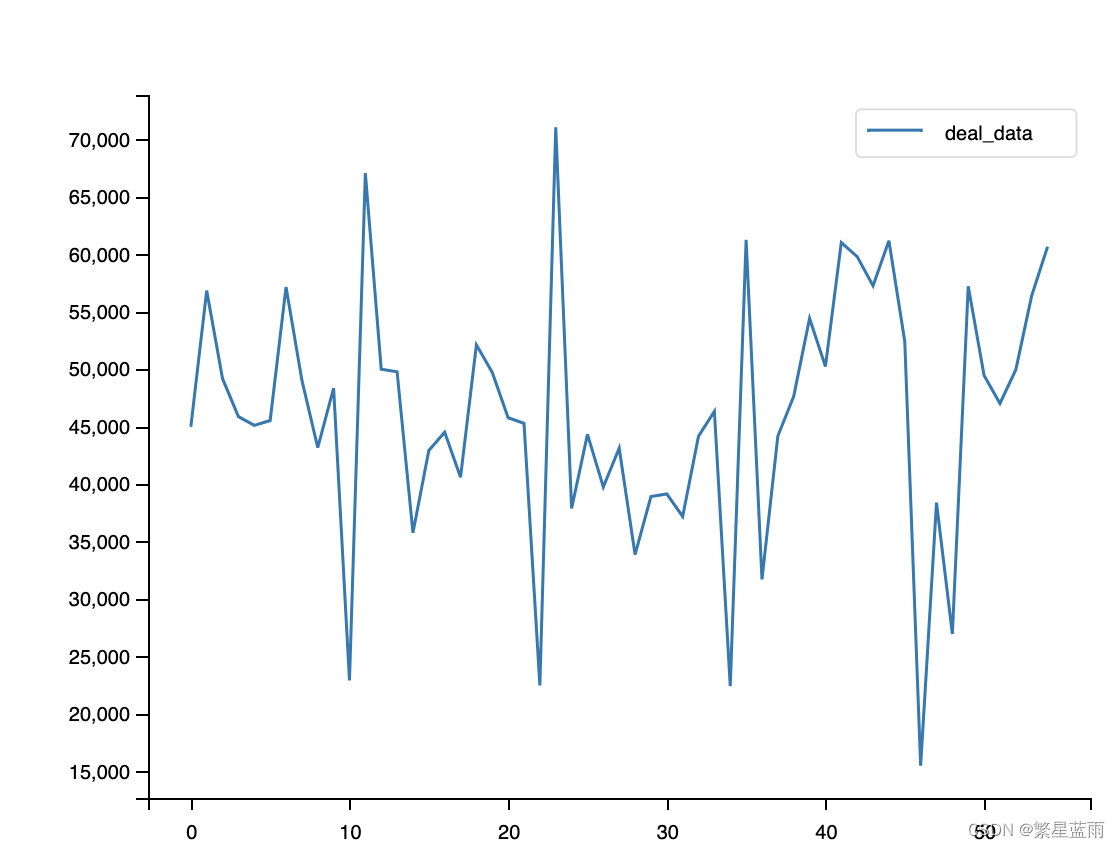
下图为自相关图：


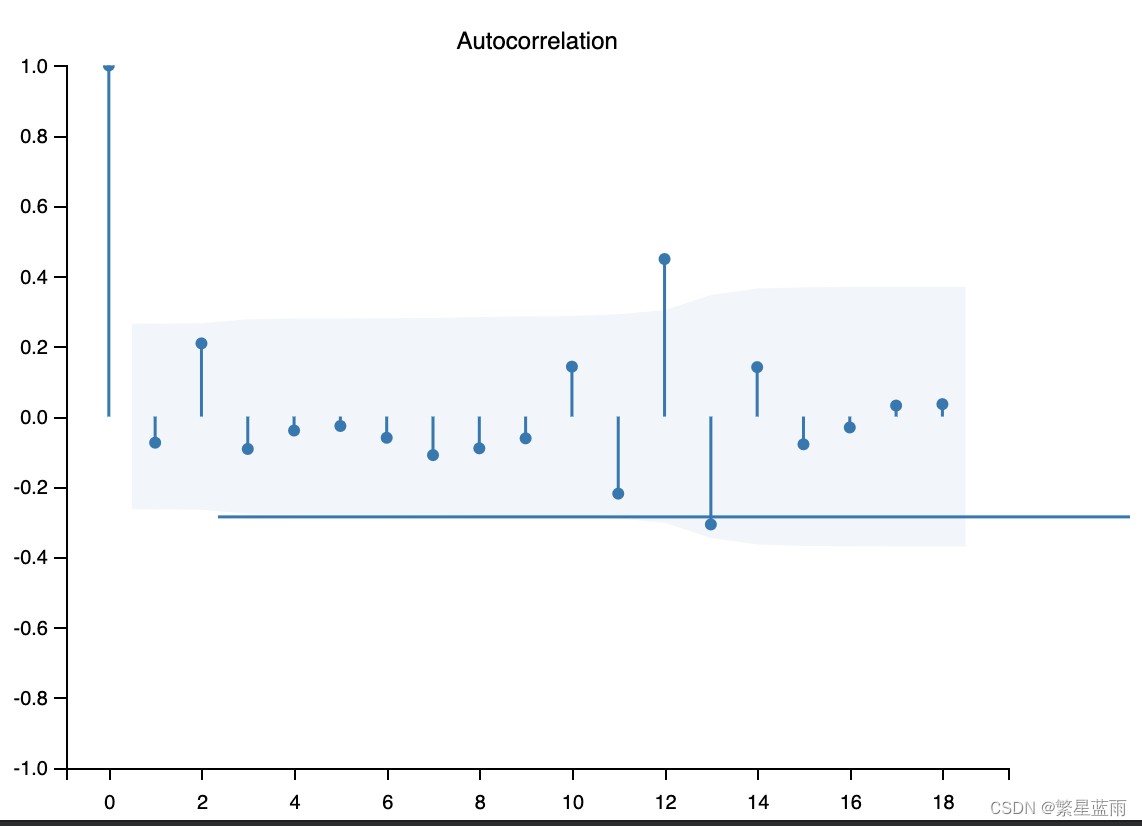
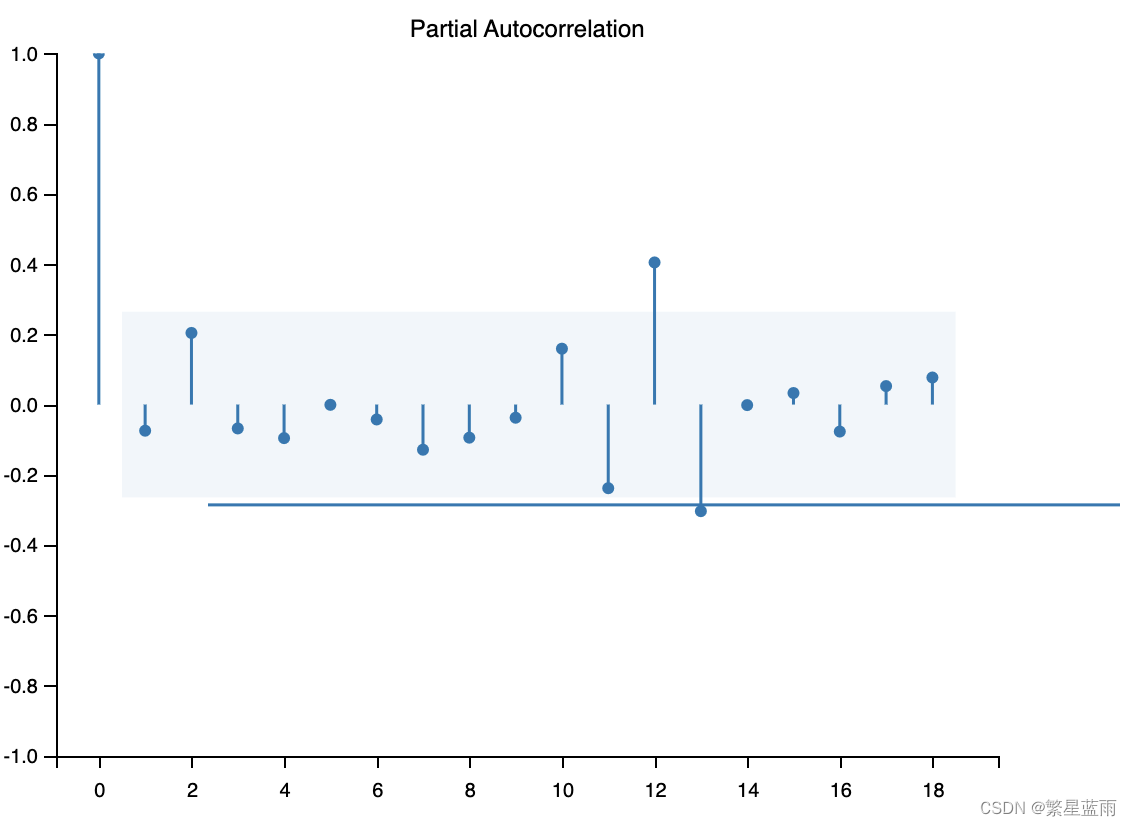
截尾

---------------------ADF检验结果----------------------
ADF Statistic(T-value): -1.065624
p-value: 0.728584
Lags Used: 11
Observations Used: 43
Critical Values:1%: -3.5935%: -2.93210%: -2.604
====================================================

由于p值为0.728584，不能拒绝原假设（数据不稳定）。

4，对原始数据进行差分，让数据变成平稳时间序列；

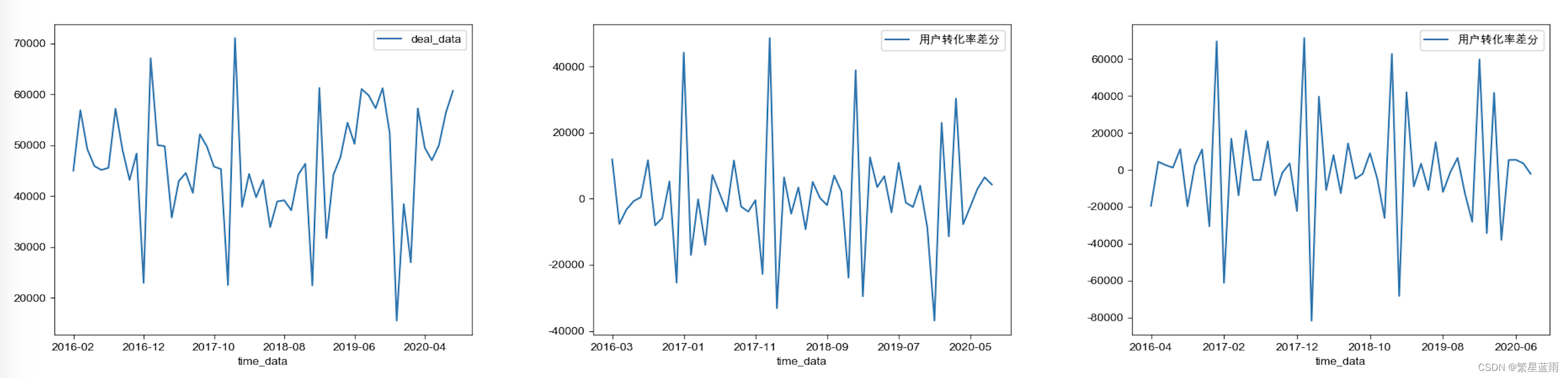
    tmp_data = data.diff().dropna()  #一阶差分并去空列D_data = tmp_data.diff().dropna()  #二阶差分tmp_data.columns = [u'用户转化率差分'] # 取列名D_data.columns = [u'用户转化率差分']# 时序图D_data.plot()plt.show()# 自相关图plot_acf(D_data).show()# 偏自相关图plot_pacf(D_data).show()print(u'一阶差分序列的ADF检验结果为：', ADF(tmp_data[u'用户转化率差分']))  # 平稳性检测print(u'二阶差分序列的ADF检验结果为：', ADF(D_data[u'用户转化率差分']))  # 平稳性检测

下图时序图(从左到右，分别为原始数据，一阶差分，二阶差分)：

可以看出数据逐渐趋于有规律

下图自相关图(从左到右，分别为原始数据，一阶差分，二阶差分)：

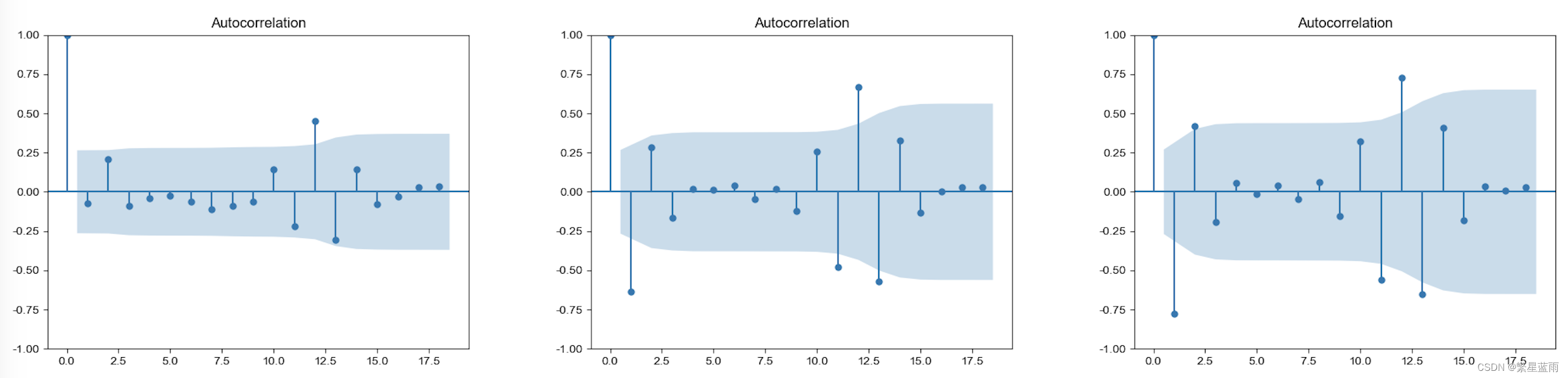
下图偏自相关图(从左到右，分别为原始数据，一阶差分，二阶差分)：

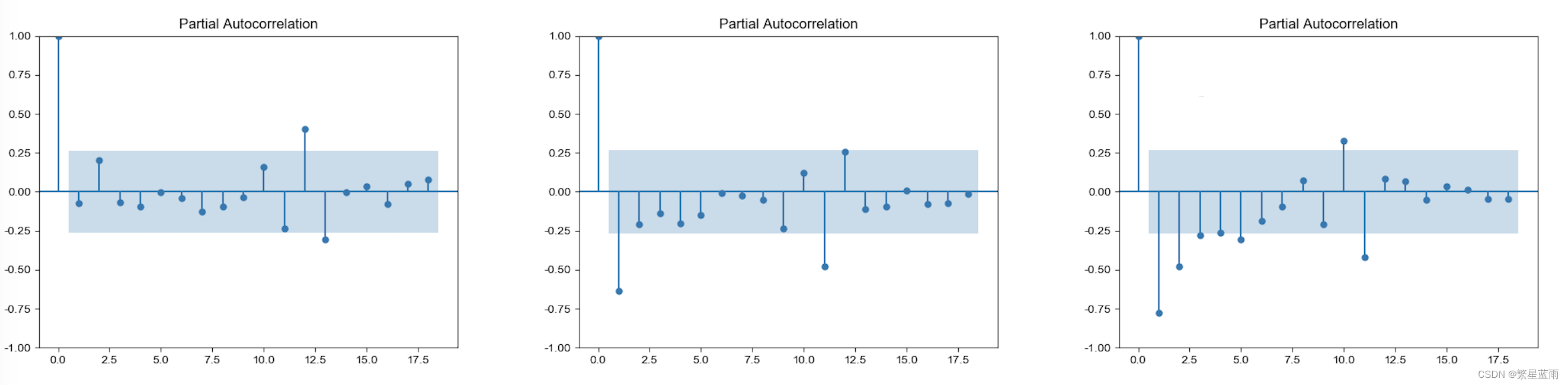
ADF检验结果：

一阶差分序列的ADF检验结果为： (-2.075566084251588, 0.25445240835460714, 11, 42, {'1%': -3.596635636000432, '5%': -2.933297331821618, '10%': -2.6049909750566895}, 891.9896110441426)
二阶差分序列的ADF检验结果为： (-5.158293394368312, 1.0689898139736479e-05, 10, 42, {'1%': -3.596635636000432, '5%': -2.933297331821618, '10%': -2.6049909750566895}, 874.5861617359358)

可以看的二阶差分后的数据的p值远远小于0.1，即可以拒绝原假设（数据不稳定），得到数据数据稳定。

5，差分序列的白噪声检验；

    print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1))  # 返回统计量和p值

运行结果

二阶差分序列的白噪声检验结果为：      lb_stat     lb_pvalue
1  33.952495  5.647422e-09

这里得到的p值为5.647422e-09，即拒绝原假设，序列不是白噪声。

6，确定ARIMA的p，q参数；

方法一（使用BIC矩阵）：

    pmax = int(len(D_data) / 10)  # 一般阶数不超过length/10qmax = int(len(D_data) / 10)  # 一般阶数不超过length/10bic_matrix = []  # BIC矩阵# 差分阶数diff_num = 2for p in range(pmax):tmp = []for q in range(qmax):try:tmp.append(ARIMA(D_data, order=(p, diff_num, q)).fit().bic)except Exception as e:print(e)tmp.append(None)bic_matrix.append(tmp)bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值p, q = bic_matrix.stack().idxmin()  # 先用stack展平，然后用idxmin找出最小值位置。print(u'BIC最小的p值和q值为：%s、%s' % (p, q))

得到结果：

BIC最小的p值和q值为：1、3

方法二：使用AIC和BIC准则定阶

    AIC = sm.tsa.stattools.arma_order_select_ic(D_data, max_ar=4, max_ma=4, ic='aic')['aic_min_order']# BICBIC = sm.tsa.stattools.arma_order_select_ic(D_data, max_ar=4, max_ma=4, ic='bic')['bic_min_order']print('---AIC与BIC准则定阶---')print('the AIC is{}\nthe BIC is{}\n'.format(AIC, BIC), end='')p = BIC[0]q = BIC[1]diff_num = 2

---AIC与BIC准则定阶---
the AIC is(0, 2)
the BIC is(0, 2)

7，模型预测；

    model = ARIMA(data, order=(p, diff_num, q)).fit()  # 建立ARIMA(p, diff+num, q)模型print('模型报告为：\n', model.summary())print("预测结果：")print(model.forecast(forecast_num))print("预测结果(详细版)：\n")forecast = model.get_forecast(steps=forecast_num)table = pd.DataFrame(forecast.summary_frame())print(table)

8，模型检验

def Model_checking(model):# 残差检验:检验残差是否服从正态分布，画图查看，然后检验# 绘制残差图model.resid.plot(figsize=(10, 3))plt.title("残差图")plt.show()print('------------残差检验-----------')# model.resid：残差 = 实际观测值 – 模型预测值print(stats.normaltest(model.resid))# QQ图看正态性qqplot(model.resid, line="q", fit=True)plt.title("Q-Q图")plt.show()# 绘制直方图plt.hist(model.resid, bins=50)plt.show()# 进行Jarque-Bera检验:判断数据是否符合总体正态分布jb_test = sm.stats.stattools.jarque_bera(model.resid)print("==================================================")print('------------Jarque-Bera检验-----------')print('Jarque-Bera test:')print('JB:', jb_test[0])print('p-value:', jb_test[1])print('Skew:', jb_test[2])print('Kurtosis:', jb_test[3])# 残差序列自相关：残差序列是否独立print('------DW检验:残差序列自相关----')print(sm.stats.stattools.durbin_watson(model.resid.values))

结果：

------------残差检验-----------
NormaltestResult(statistic=4.4959826117374515, pvalue=0.10561115214326909)------------Jarque-Bera检验-----------
Jarque-Bera test:
JB: 4.0642468241648775
p-value: 0.13105693759455012
Skew: 0.33412880151714236
Kurtosis: 4.151920700073933------DW检验:残差序列自相关----
1.71022123825392

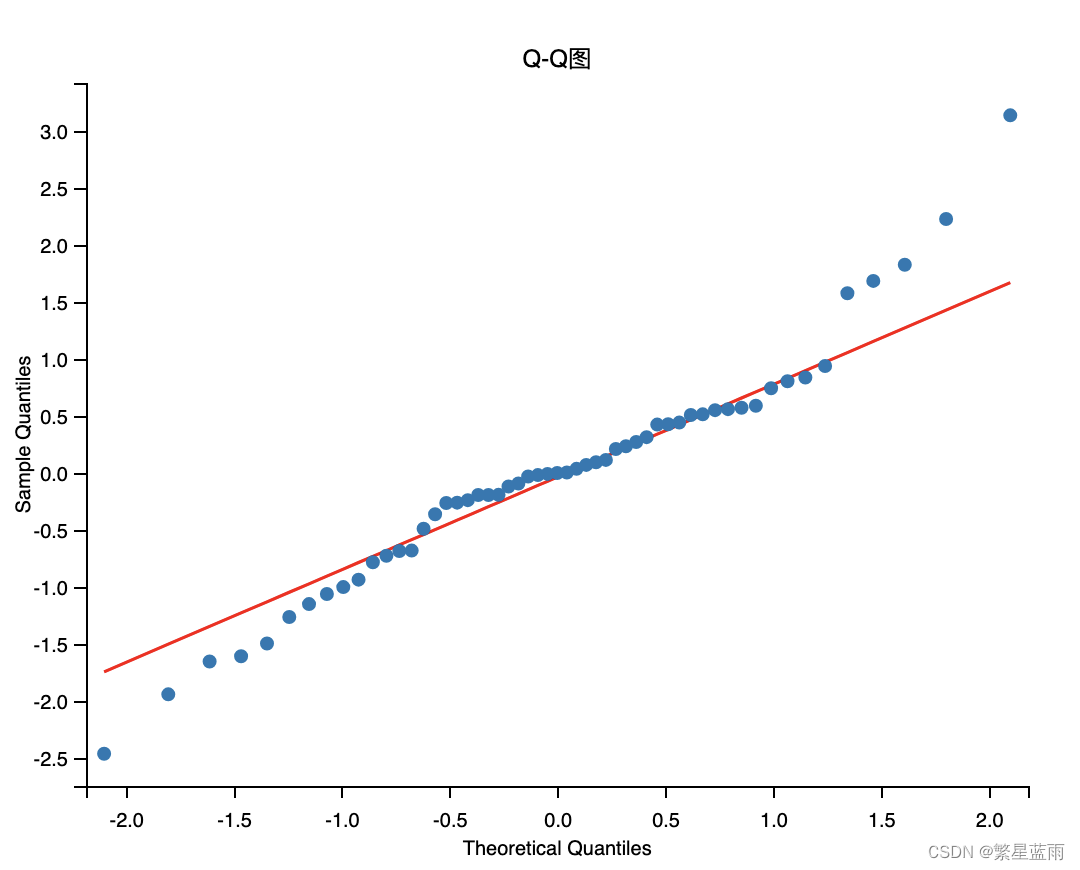
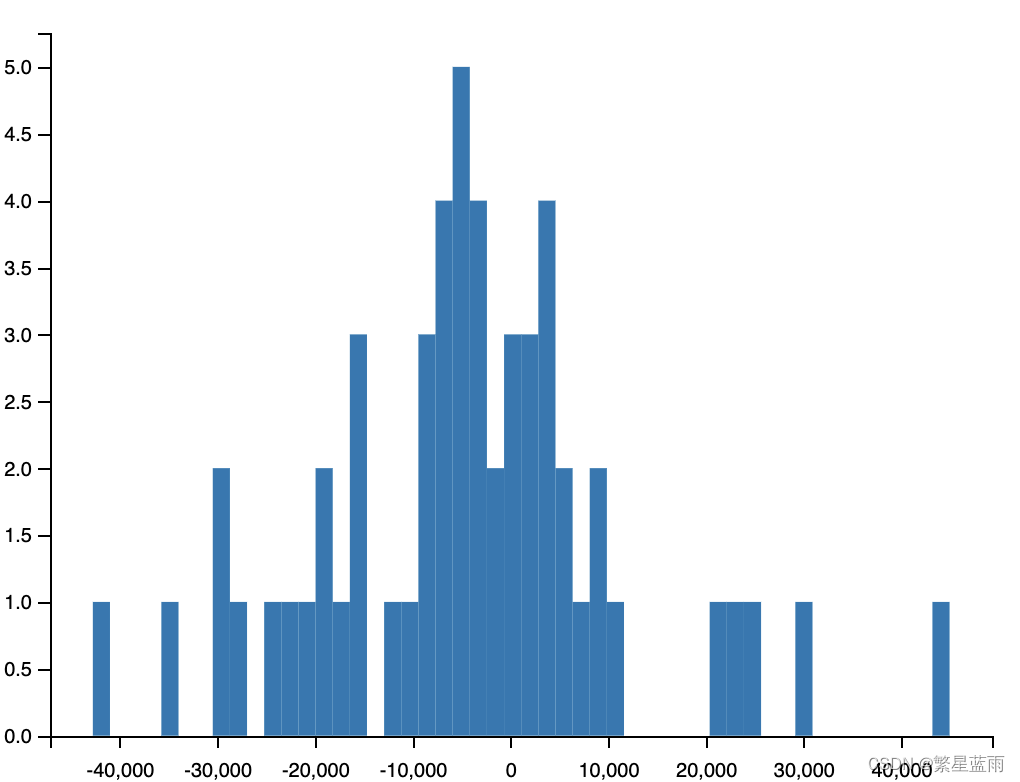
由检测结果可以看出，模式良好。

3.2 完整代码

from __future__ import annotations
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf #ACF与PACF
from statsmodels.tsa.arima.model import ARIMA #ARIMA模型
from statsmodels.graphics.api import qqplot  #qq图
from scipy import statsimport warnings
warnings.filterwarnings("ignore")# 绘图设置（适用于mac）
# plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号# 模型检测
def Model_checking(model) -> None:# 残差检验:检验残差是否服从正态分布，画图查看，然后检验print('------------残差检验-----------')# model.resid：残差 = 实际观测值 – 模型预测值print(stats.normaltest(model.resid))# QQ图看正态性qqplot(model.resid, line="q", fit=True)plt.title("Q-Q图")plt.show()# 绘制直方图plt.hist(model.resid, bins=50)plt.show()# 进行Jarque-Bera检验:判断数据是否符合总体正态分布jb_test = sm.stats.stattools.jarque_bera(model.resid)print("==================================================")print('------------Jarque-Bera检验-----------')print('Jarque-Bera test:')print('JB:', jb_test[0])print('p-value:', jb_test[1])print('Skew:', jb_test[2])print('Kurtosis:', jb_test[3])# 残差序列自相关：残差序列是否独立print("==================================================")print('------DW检验:残差序列自相关----')print(sm.stats.stattools.durbin_watson(model.resid.values))# 使用BIC矩阵计算p和q的值
def cal_pqValue(D_data, diff_num=0) -> List[float]:# 定阶pmax = int(len(D_data) / 10)  # 一般阶数不超过length/10qmax = int(len(D_data) / 10)  # 一般阶数不超过length/10bic_matrix = []  # BIC矩阵# 差分阶数diff_num = 2for p in range(pmax + 1):tmp = []for q in range(qmax + 1):try:tmp.append(ARIMA(D_data, order=(p, diff_num, q)).fit().bic)except Exception as e:print(e)tmp.append(None)bic_matrix.append(tmp)bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值p, q = bic_matrix.stack().idxmin()  # 先用stack展平，然后用idxmin找出最小值位置。print(u'BIC最小的p值和q值为：%s、%s' % (p, q))return p, q# 计算时序序列模型
def cal_time_series(data, forecast_num=3) -> None:# 绘制时序图data.plot()# 存储图片plt.savefig('/Users/mac/Downloads/1.png')plt.show()# 绘制自相关图plot_acf(data).show()# 绘制偏自相关图plot_pacf(data).show()# 时序数据平稳性检测original_ADF = ADF(data[u'deal_data'])print(u'原始序列的ADF检验结果为：', original_ADF)# 对数序数据进行d阶差分运算，化为平稳时间序列diff_num = 0 # 差分阶数diff_data = data     # 差分数序数据ADF_p_value = ADF(data[u'deal_data'])[1]while  ADF_p_value > 0.01:diff_data = diff_data.diff(periods=1).dropna()diff_num = diff_num + 1ADF_result = ADF(diff_data[u'deal_data'])ADF_p_value = ADF_result[1]print("ADF_p_value:{ADF_p_value}".format(ADF_p_value=ADF_p_value))print(u'{diff_num}差分的ADF检验结果为：'.format(diff_num = diff_num), ADF_result )# 白噪声检测print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(diff_data, lags=1))  # 返回统计量和p值# 使用AIC和BIC准则定阶q和p的值(推荐)AIC = sm.tsa.stattools.arma_order_select_ic(diff_data, max_ar=4, max_ma=4, ic='aic')['aic_min_order']BIC = sm.tsa.stattools.arma_order_select_ic(diff_data, max_ar=4, max_ma=4, ic='bic')['bic_min_order']print('---AIC与BIC准则定阶---')print('the AIC is{}\nthe BIC is{}\n'.format(AIC, BIC), end='')p = BIC[0]q = BIC[1]# 使用BIC矩阵来计算q和p的值# pq_result = cal_pqValue(diff_data, diff_num)# p = pq_result[0]# q = pq_result[1]# 构建时间序列模型model = ARIMA(data, order=(p, diff_num, q)).fit()  # 建立ARIMA(p, diff+num, q)模型print('模型报告为：\n', model.summary())print("预测结果：\n", model.forecast(forecast_num))print("预测结果(详细版)：\n")forecast = model.get_forecast(steps=forecast_num)table = pd.DataFrame(forecast.summary_frame())print(table)# 绘制残差图diff_data.plot(color='orange', title='残差图')model.resid.plot(figsize=(10, 3))plt.title("残差图")# plt.savefig('/Users/mac/Downloads/1.png')plt.show()# 模型检查Model_checking(model)if __name__ == '__main__':# 数据测试1:need_data = {'2016-02': 44964.03, '2016-03': 56825.51, '2016-04': 49161.98, '2016-05': 45859.35,'2016-06': 45098.56,'2016-07': 45522.17, '2016-08': 57133.18, '2016-09': 49037.29, '2016-10': 43157.36,'2016-11': 48333.17,'2016-12': 22900.94,'2017-01': 67057.29, '2017-02': 49985.29, '2017-03': 49771.47, '2017-04': 35757.0, '2017-05': 42914.27,'2017-06': 44507.03, '2017-07': 40596.51, '2017-08': 52111.75, '2017-09': 49711.18,'2017-10': 45766.09,'2017-11': 45273.82, '2017-12': 22469.57,'2018-01': 71032.23, '2018-02': 37874.38, '2018-03': 44312.24, '2018-04': 39742.02,'2018-05': 43118.38,'2018-06': 33859.69, '2018-07': 38910.89, '2018-08': 39138.42, '2018-09': 37175.03,'2018-10': 44159.96,'2018-11': 46321.72, '2018-12': 22410.88,'2019-01': 61241.94, '2019-02': 31698.6, '2019-03': 44170.62, '2019-04': 47627.13, '2019-05': 54407.37,'2019-06': 50231.68, '2019-07': 61010.29, '2019-08': 59782.19, '2019-09': 57245.15,'2019-10': 61162.55,'2019-11': 52398.25, '2019-12': 15482.64,'2020-01': 38383.97, '2020-02': 26943.55, '2020-03': 57200.32, '2020-04': 49449.95,'2020-05': 47009.84,'2020-06': 49946.25, '2020-07': 56383.23, '2020-08': 60651.07}data = {'time_data': list(need_data.keys()), 'deal_data': list(need_data.values())}df = pd.DataFrame(data)df.set_index(['time_data'], inplace=True)  # 设置索引cal_time_series(df, 7) # 模型调用# 数据测试2（从excel中读取）:# path = '/Users/mac/Downloads/时间序列模型测试数据.xlsx'# df = pd.read_excel(path)# df.rename(columns={'data': 'deal_data', 'time': 'time_data'}, inplace=True)# df.set_index(['time_data'], inplace=True)  # 设置索引# cal_time_series(df, 7) # 模型调用

4 测试数据和完整代码

网盘链接：提取码: o8po

参考文章

图灵追慕者
SPSSPRO​
Github上facebook的prophet项目
Yuting_Sunshine
一眉师傅
English Chan
Sany 何灿
机器之心
seriesc
北京大学《金融时间序列分析讲义》
Foneone
statsmodels中文官网API

这篇关于Python实现时间序列ARIMA模型（附带超详细理论知识和完整代码实现）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---