本文主要是介绍Python数学建模学习-PageRank算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1-基本概念
PageRank算法是由Google创始人Larry Page在斯坦福大学时提出,又称PR,佩奇排名。主要针对网页进行排名,计算网站的重要性,优化搜索引擎的搜索结果。PR值是表示其重要性的因子。
中心思想:
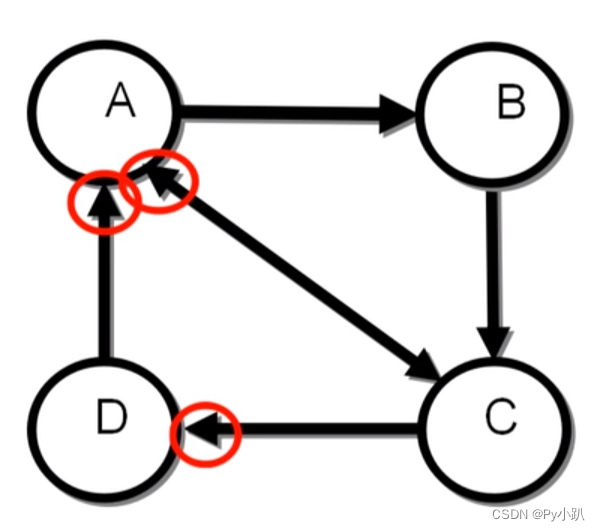
- 数量假设:在网页模型图中,一个网页接受到的其他网页指向的入链(In-Links)越多,说明该网页越重要。

- 质量假设:当一个质量高的网页指向(Out-Links)一个网页,说明这个被指的网页重要。

- 入链出链模型图1:
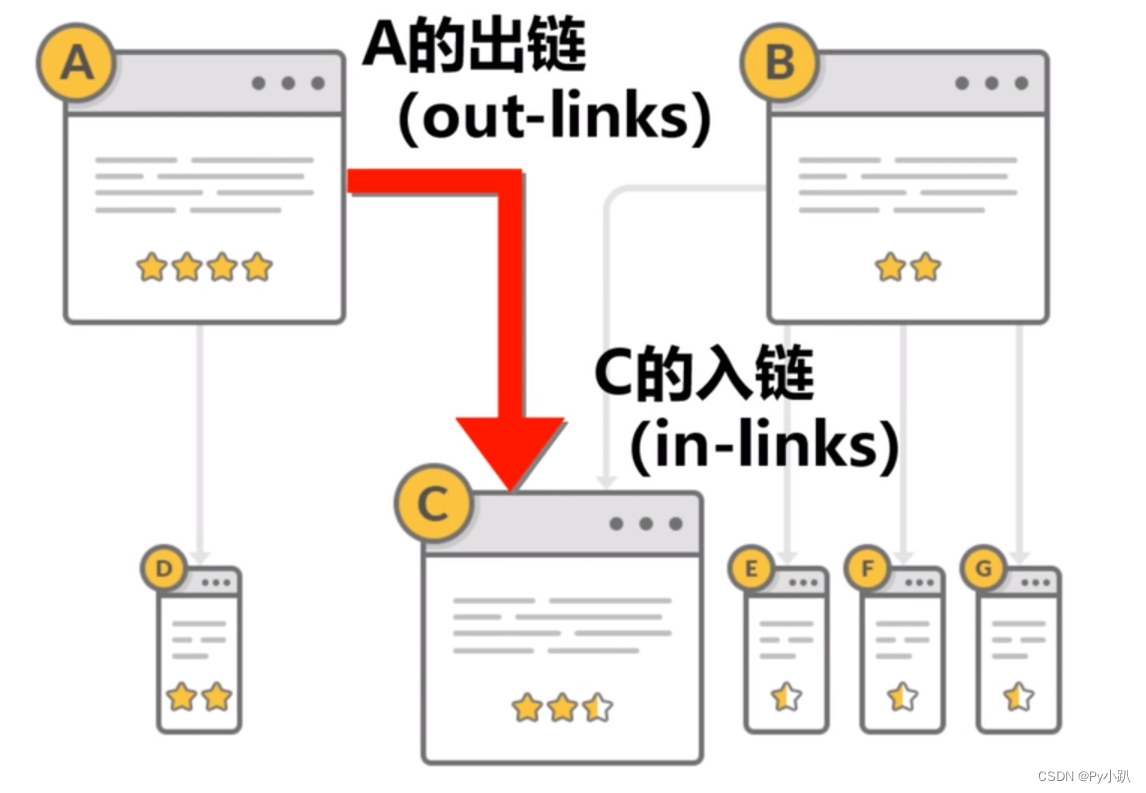
- 入链出链模型图2:[把每个网页当成一个节点]
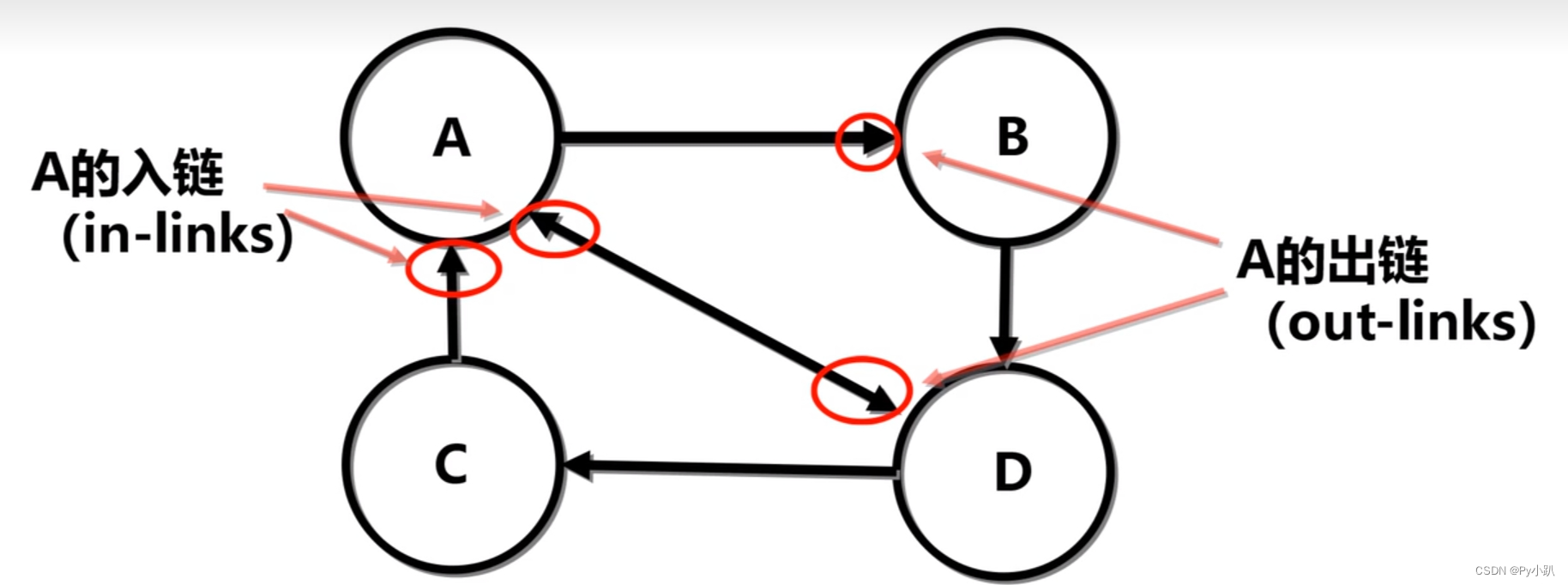
2-算法和公式
PageRank公式
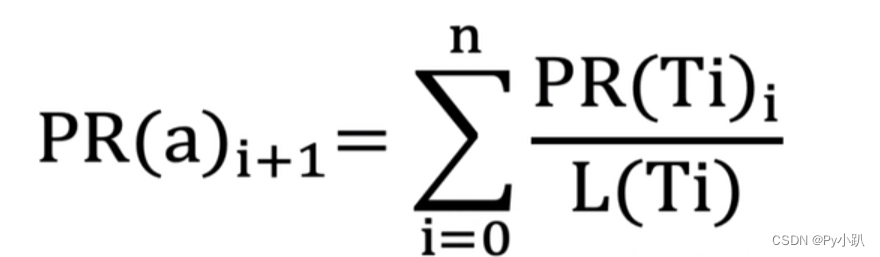
- PR(Ti)代表的是其他节点的(指向A节点)PR值
- L(Ti)代表的是其他节点的(指向A节点)出链数
- i 代表的是循环次数
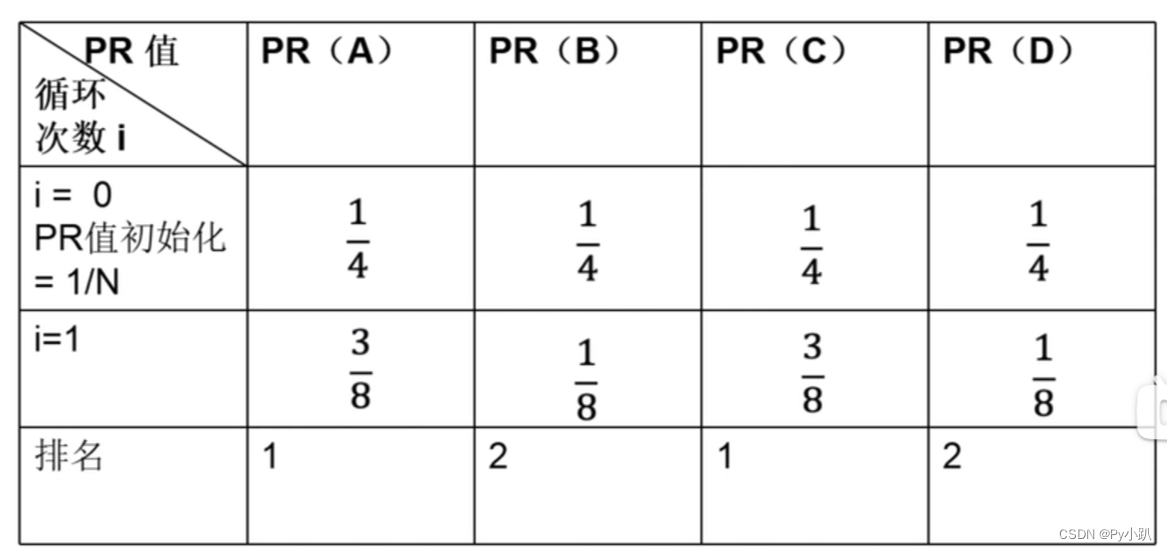
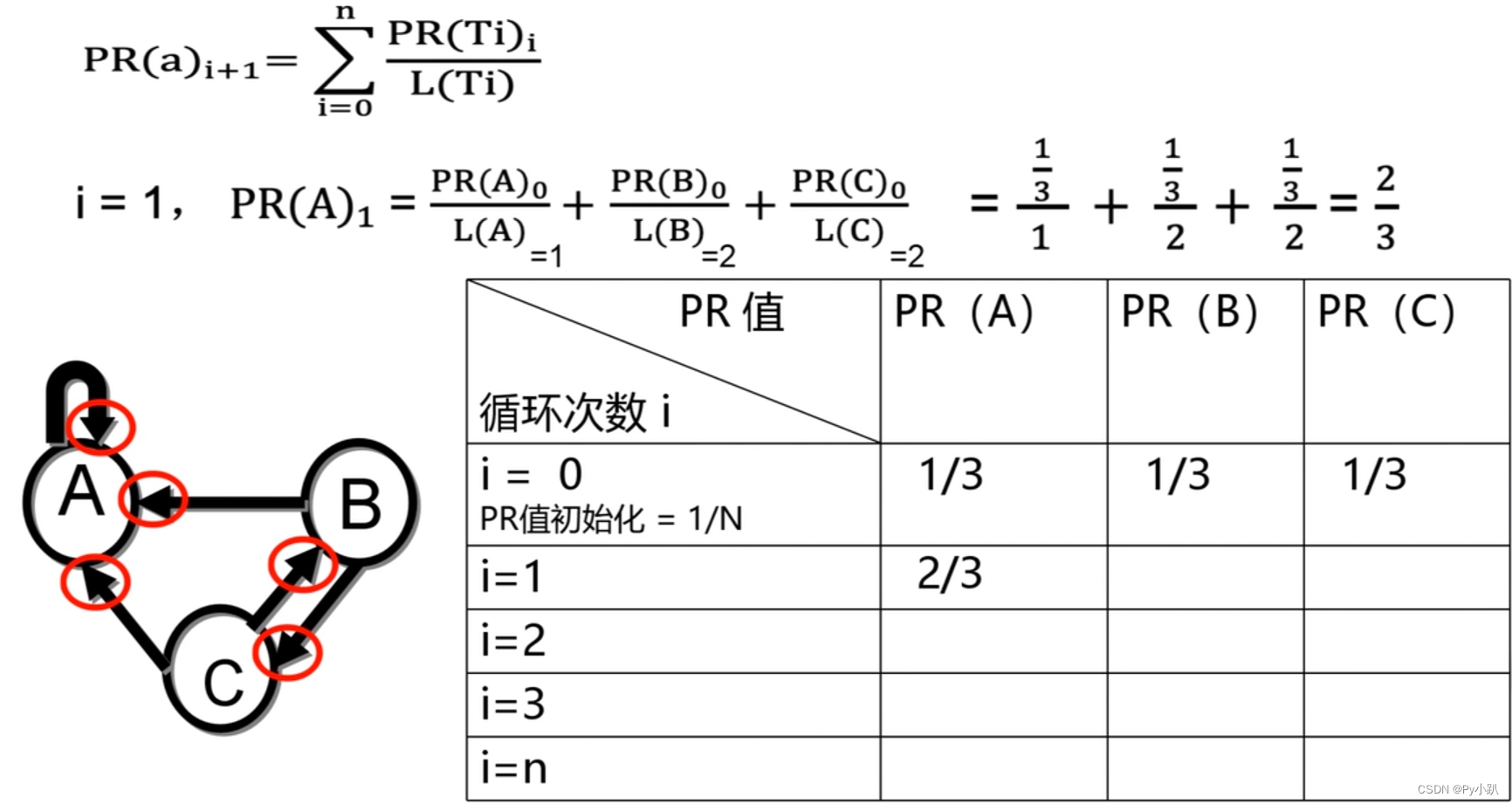
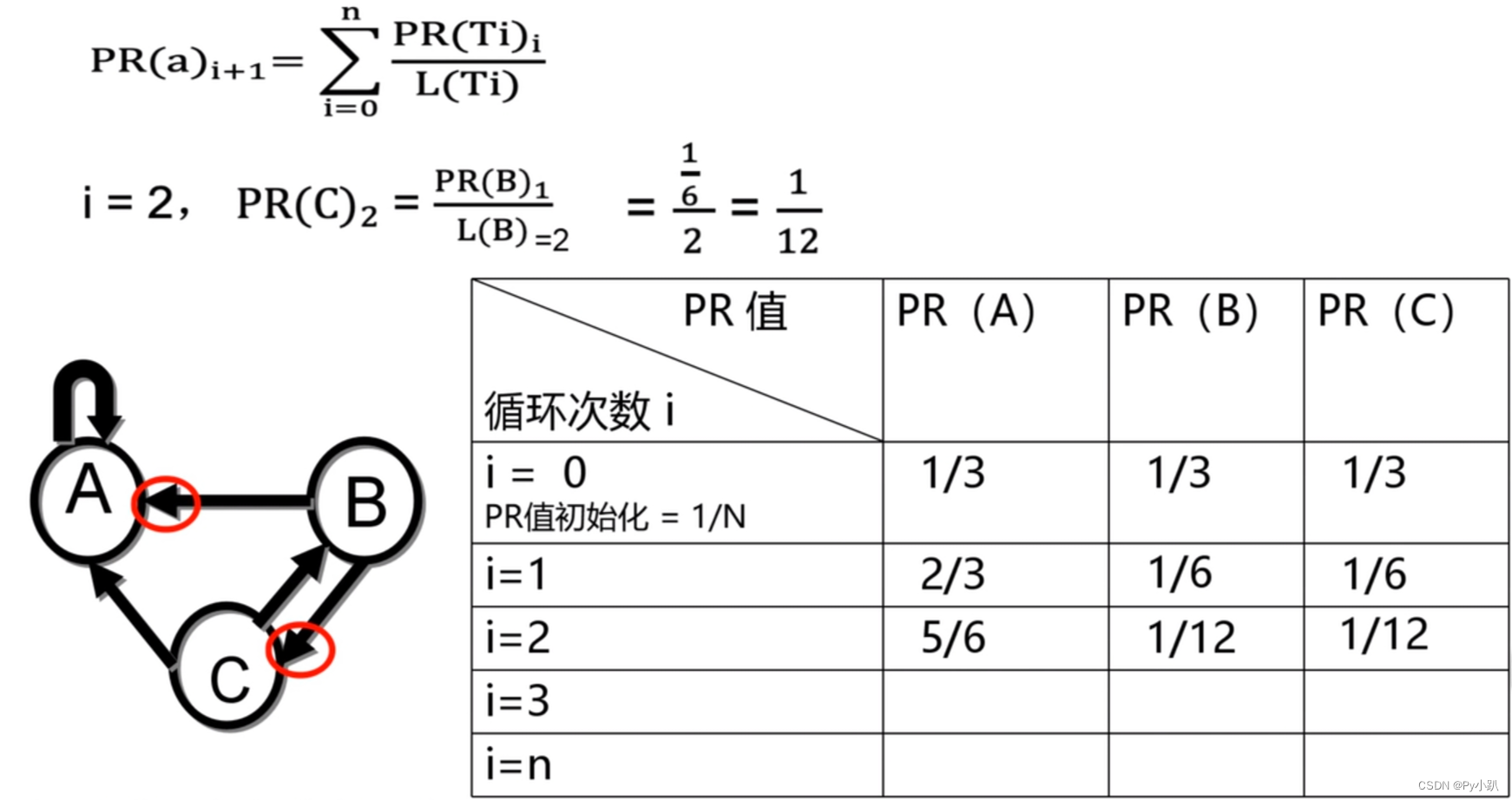
i=0时,
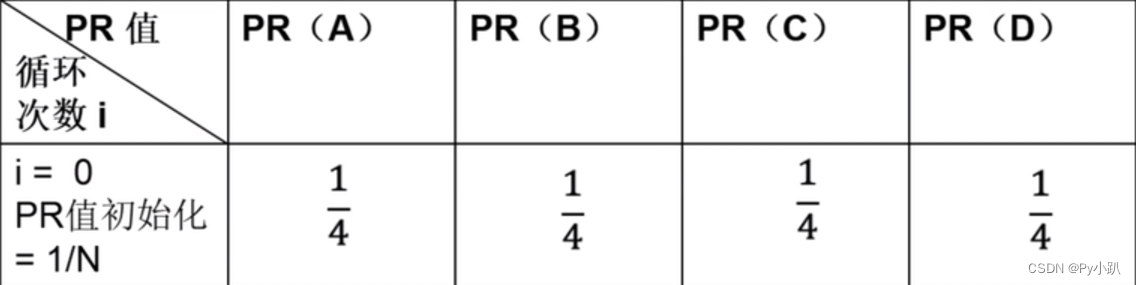
i=1时,PR(A)为:
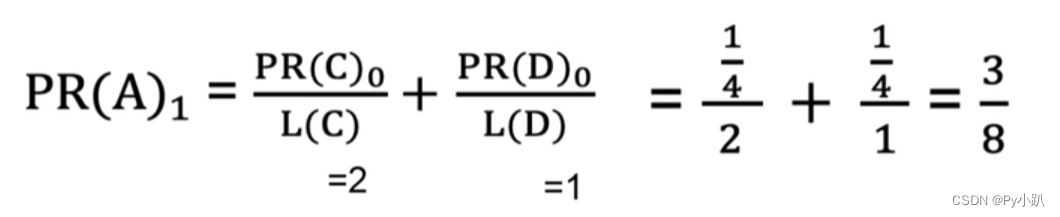
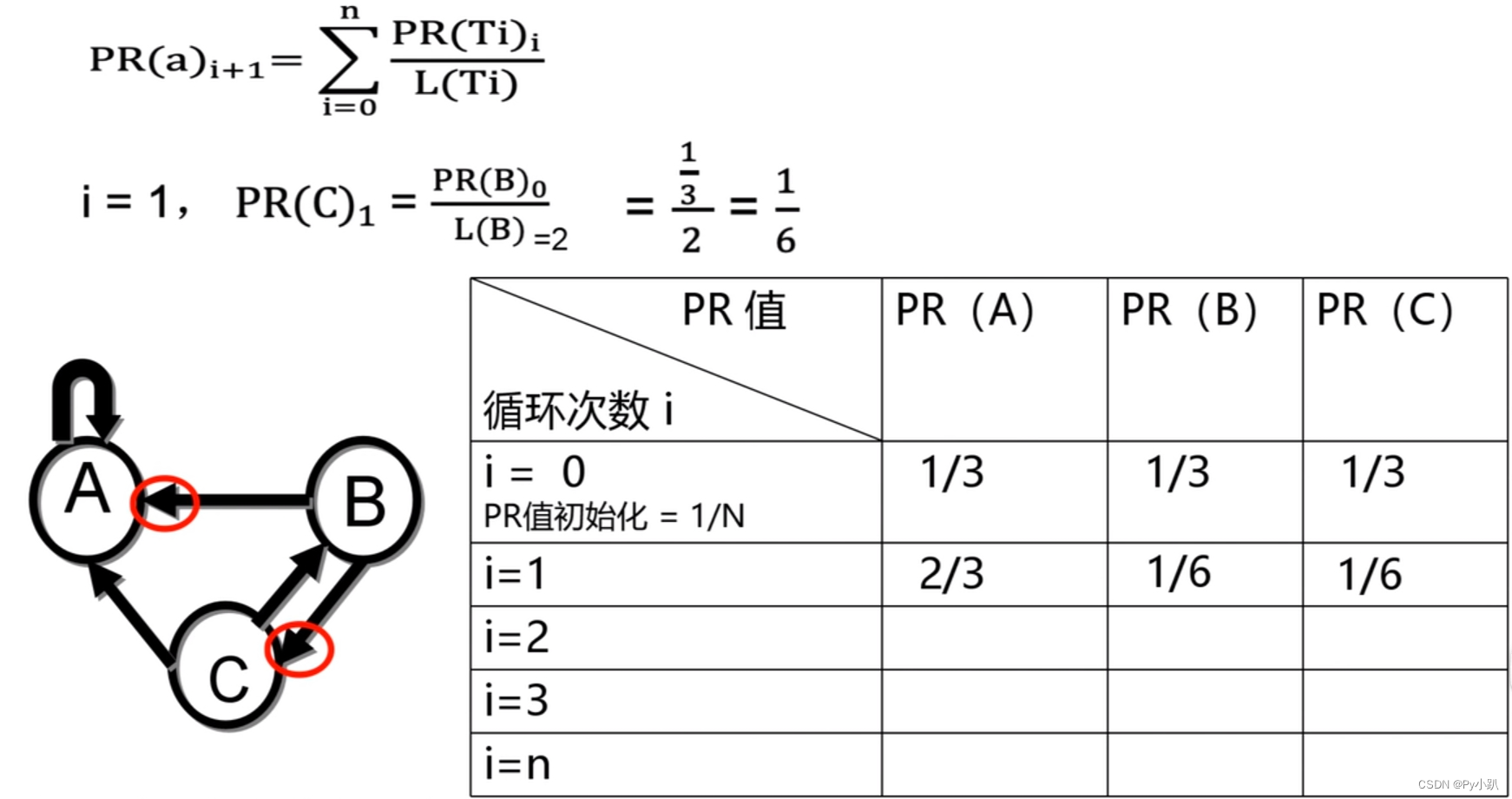
i=1时,PR(B)为:
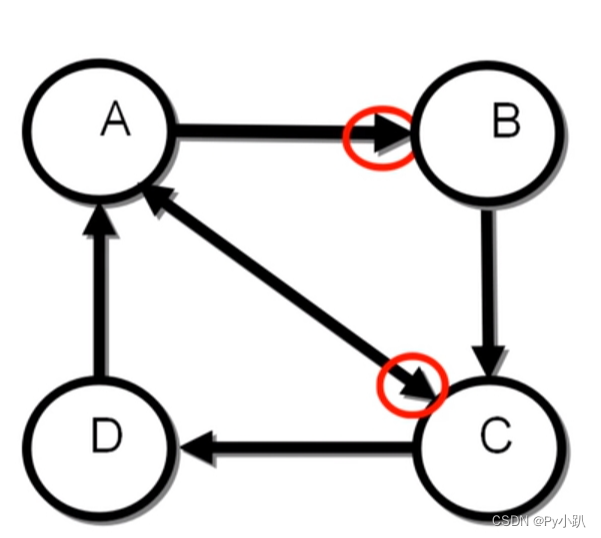

i=1时,PR(C)为:
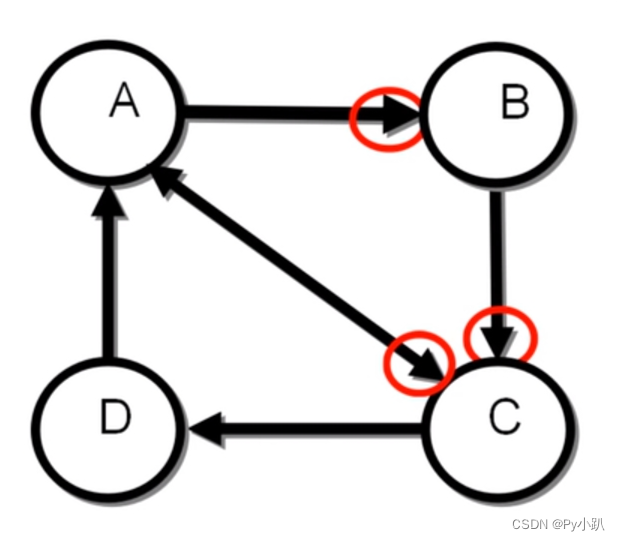
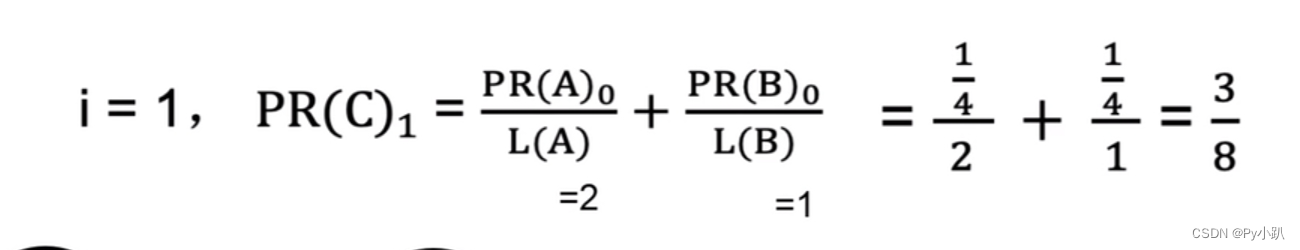
i=1时,PR(D)为:

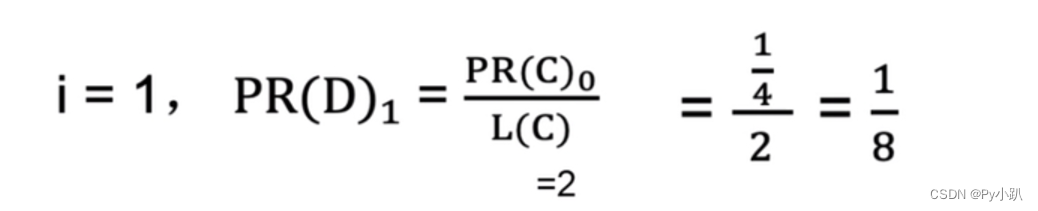
主要找到入链数和出链数
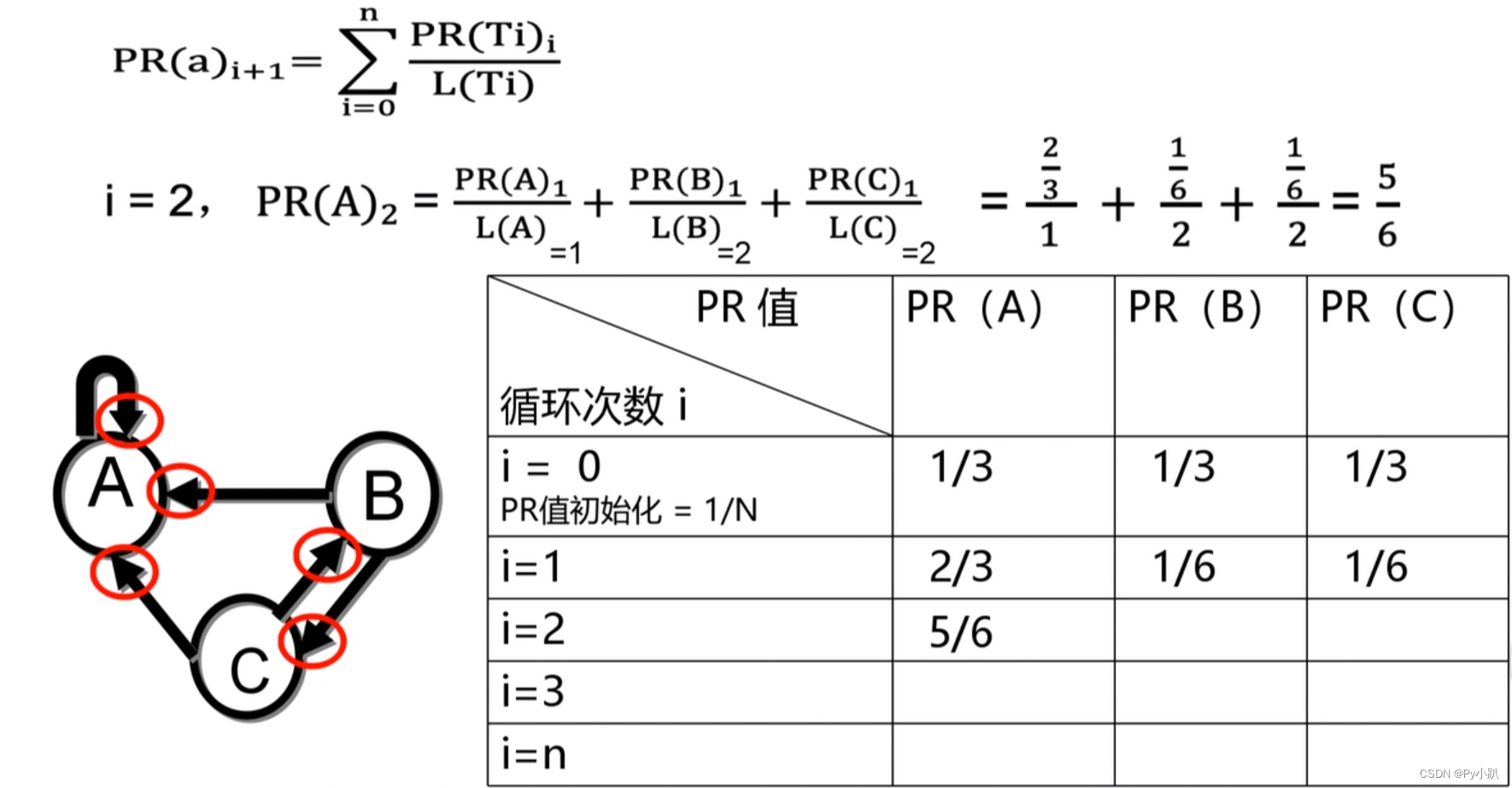
可以求得:
矩阵化表达:使用转移概率矩阵/马尔可夫矩阵
将左图内容转换为右图矩阵:

从图可以看出:
从A将跳转到B或C的概率为1/2

从B将跳转到C的概率为1
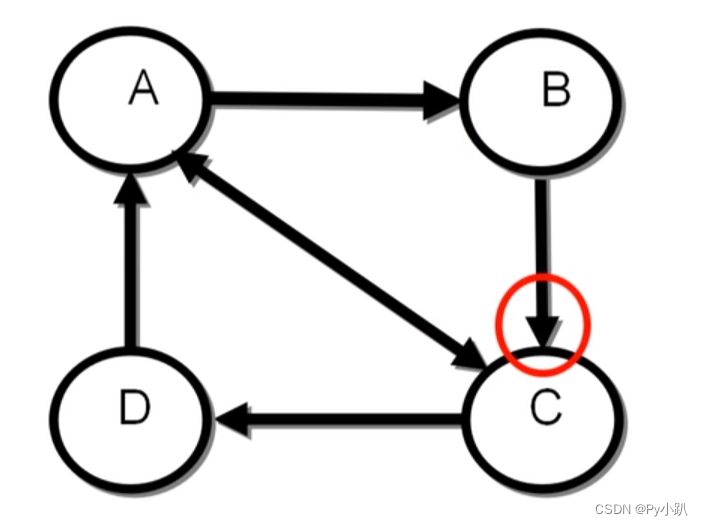
从C将跳转到A或D的概率为1/2

从D将跳转到A的概率为1

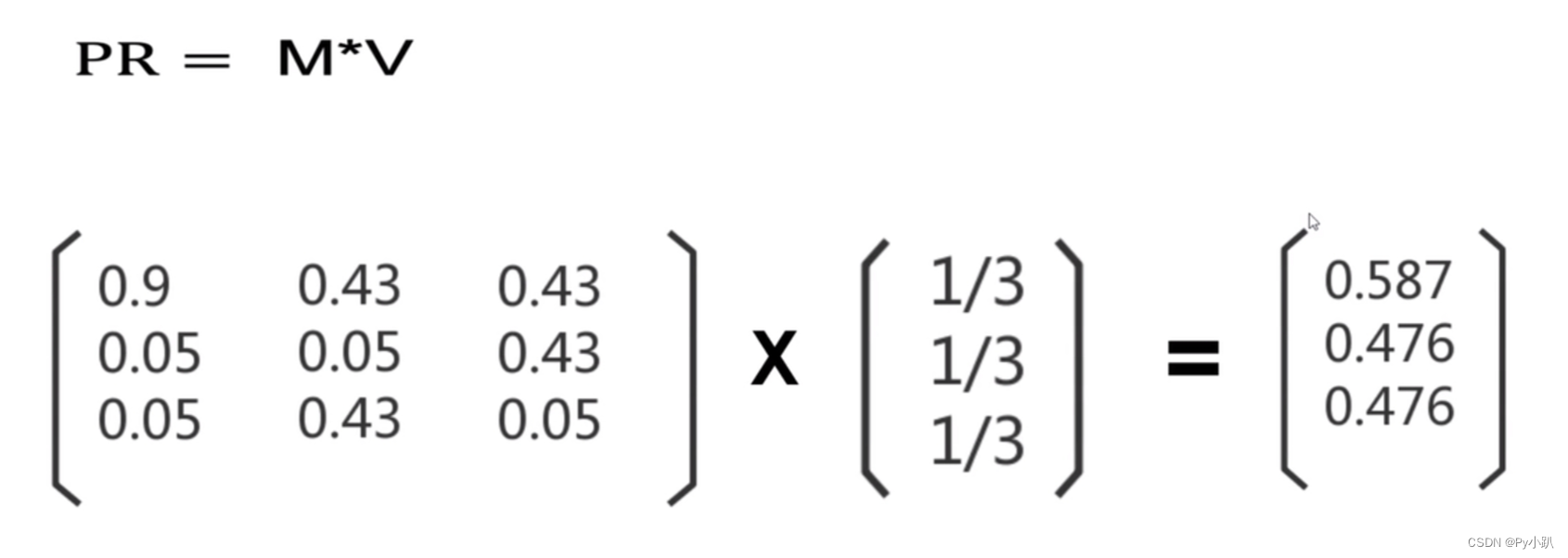
通过矩阵表达快速计算PR值
公式:
其中 表示转移概率矩阵/马尔可夫矩阵

其中 表示上一次得到的PR值

根据公式可得第一次迭代得到的PR值:

0*1/4+0*1/4+1/2*1/4+1*1/4=3/8
1/2*1/4+ 0*1/4+0*1/4+0*1/4=1/8
1/2*1/4+ 1*1/4+0*1/4+0*1/4=3/8
0*1/4+0*1/4+1/2*1/4+0*1/4=1/8
通过第一次迭代得到的PR值,我们可以得到第二次迭代的PR值:

此时的排名为:
AC;BD
再结合最开始的公式看:

同理可求出其他PR值。
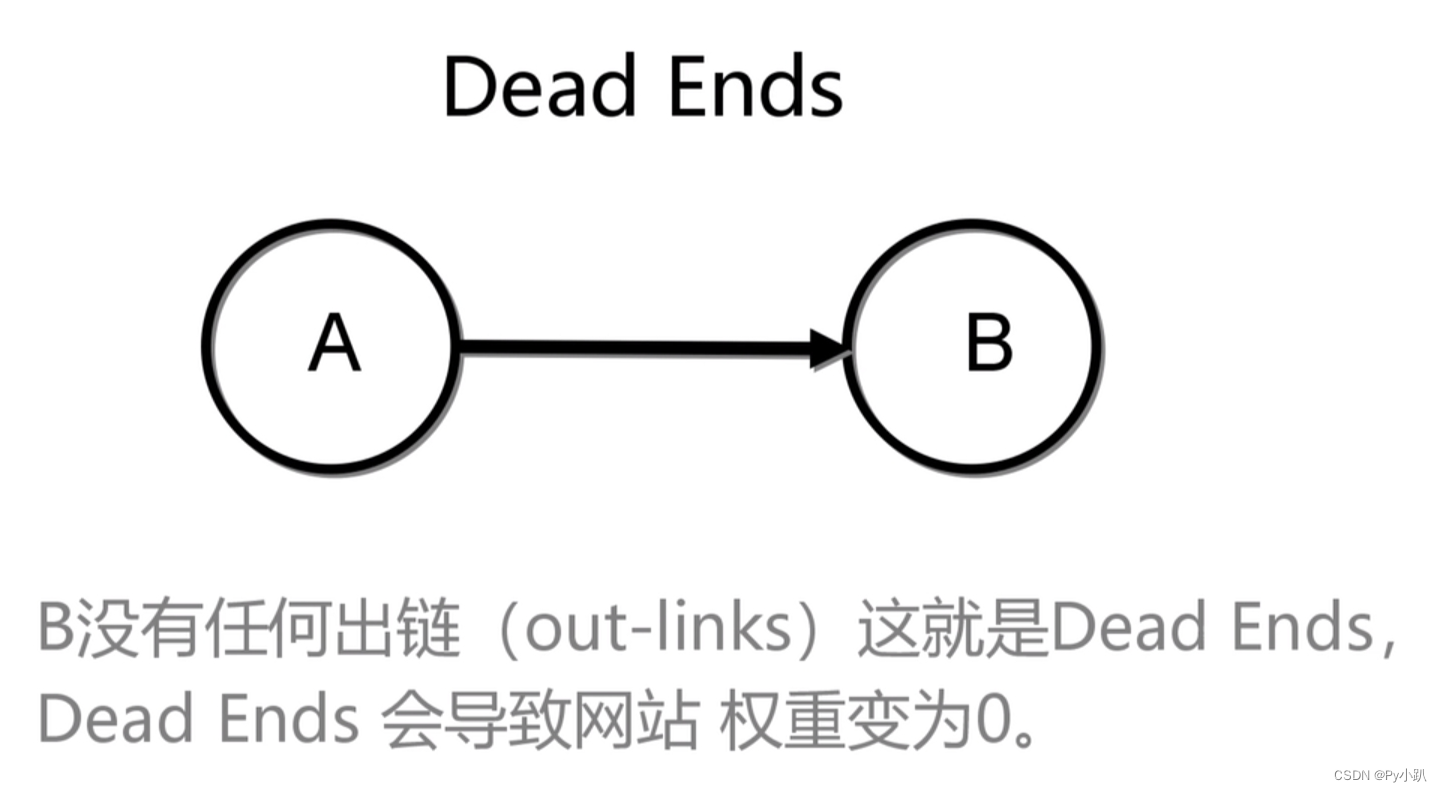
3-Dead Ends 问题
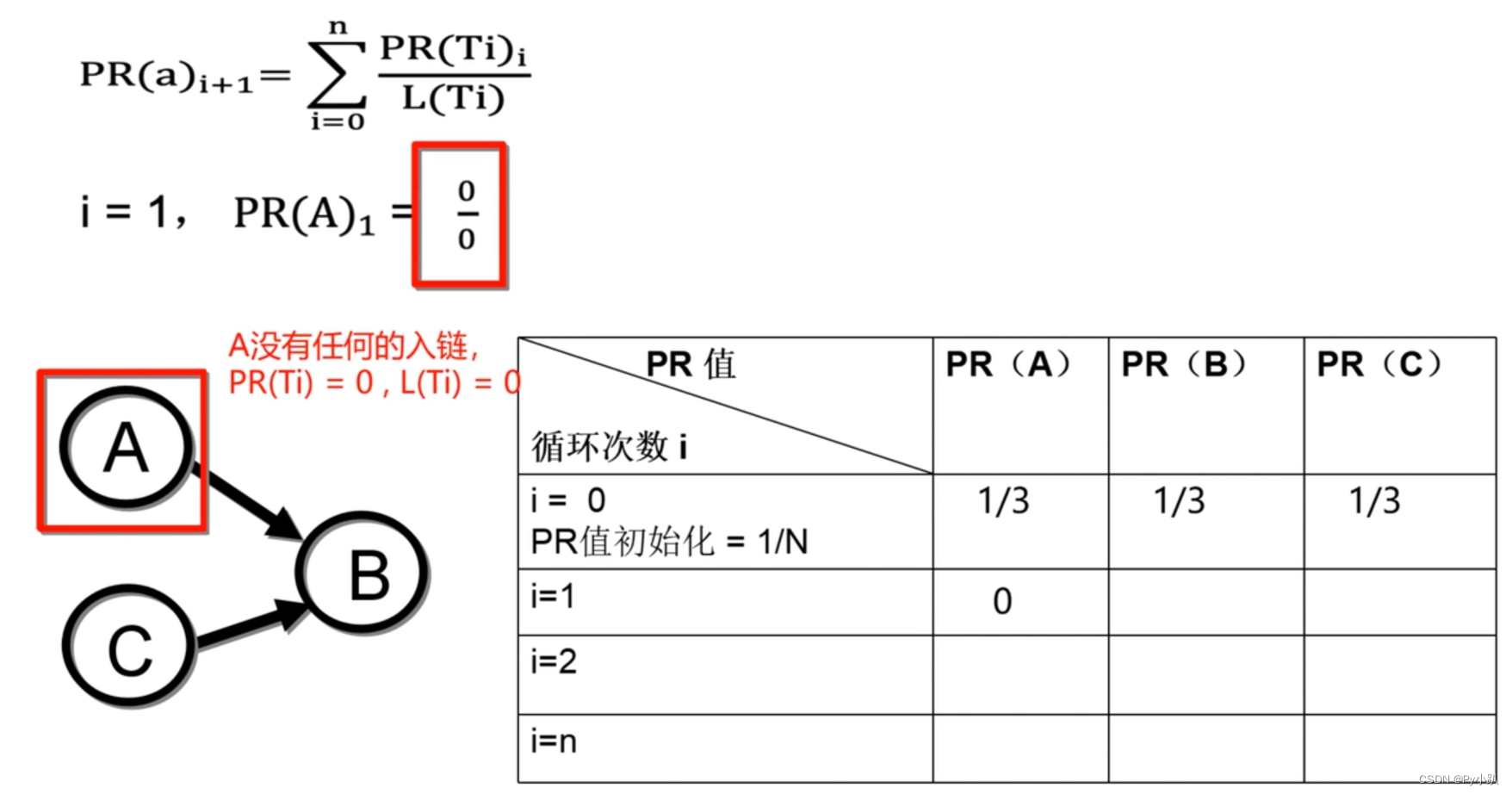
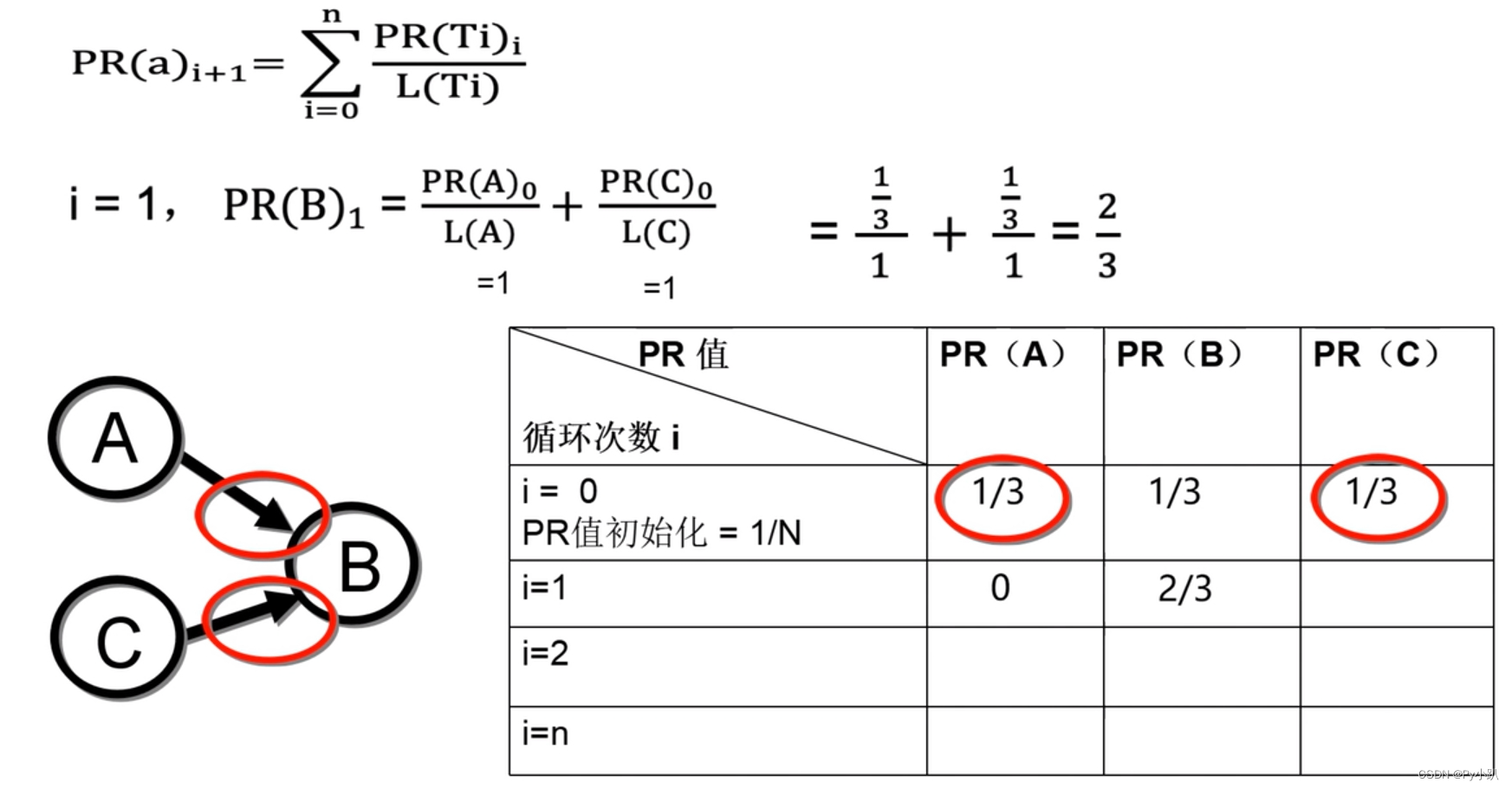
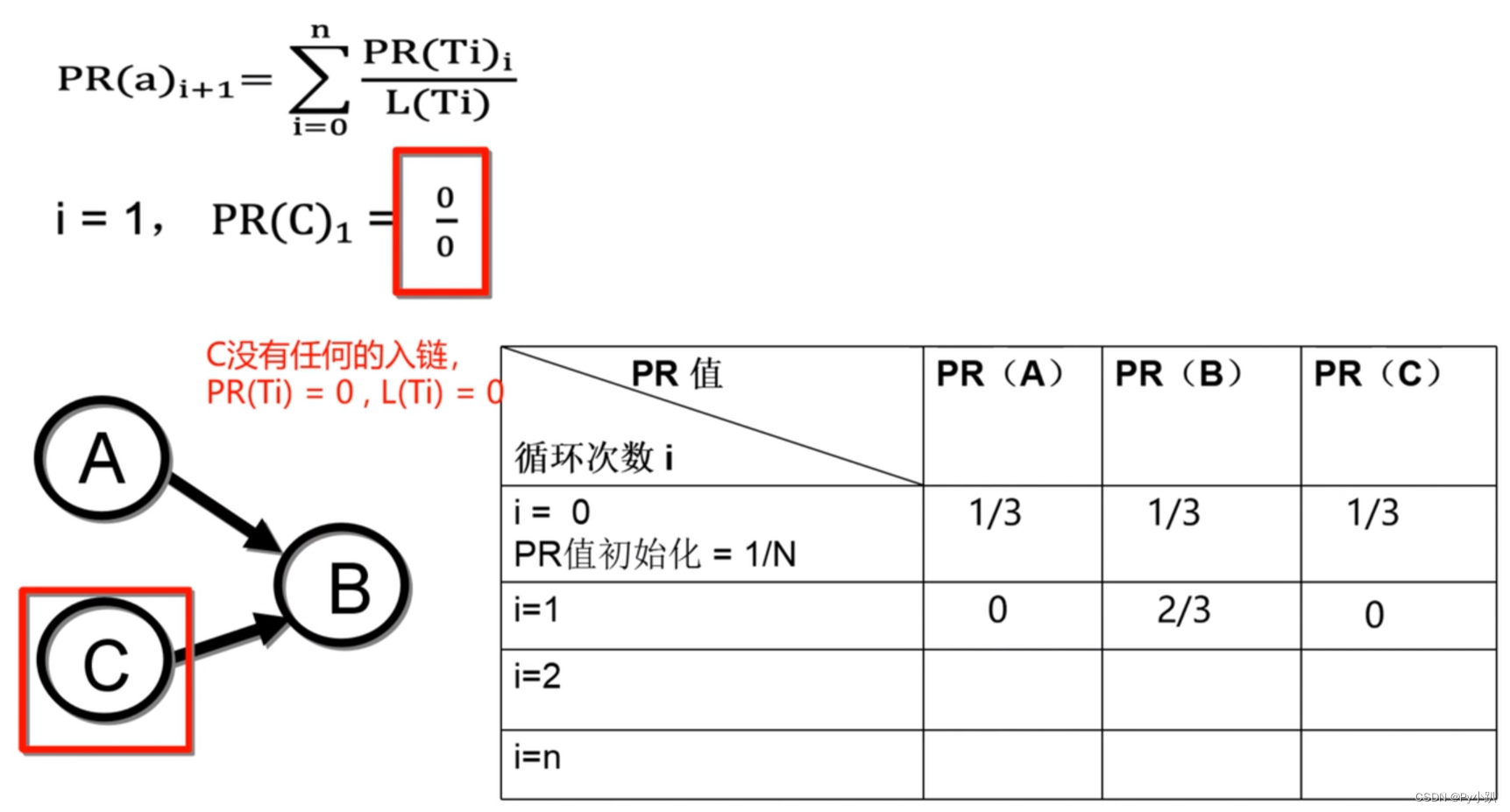
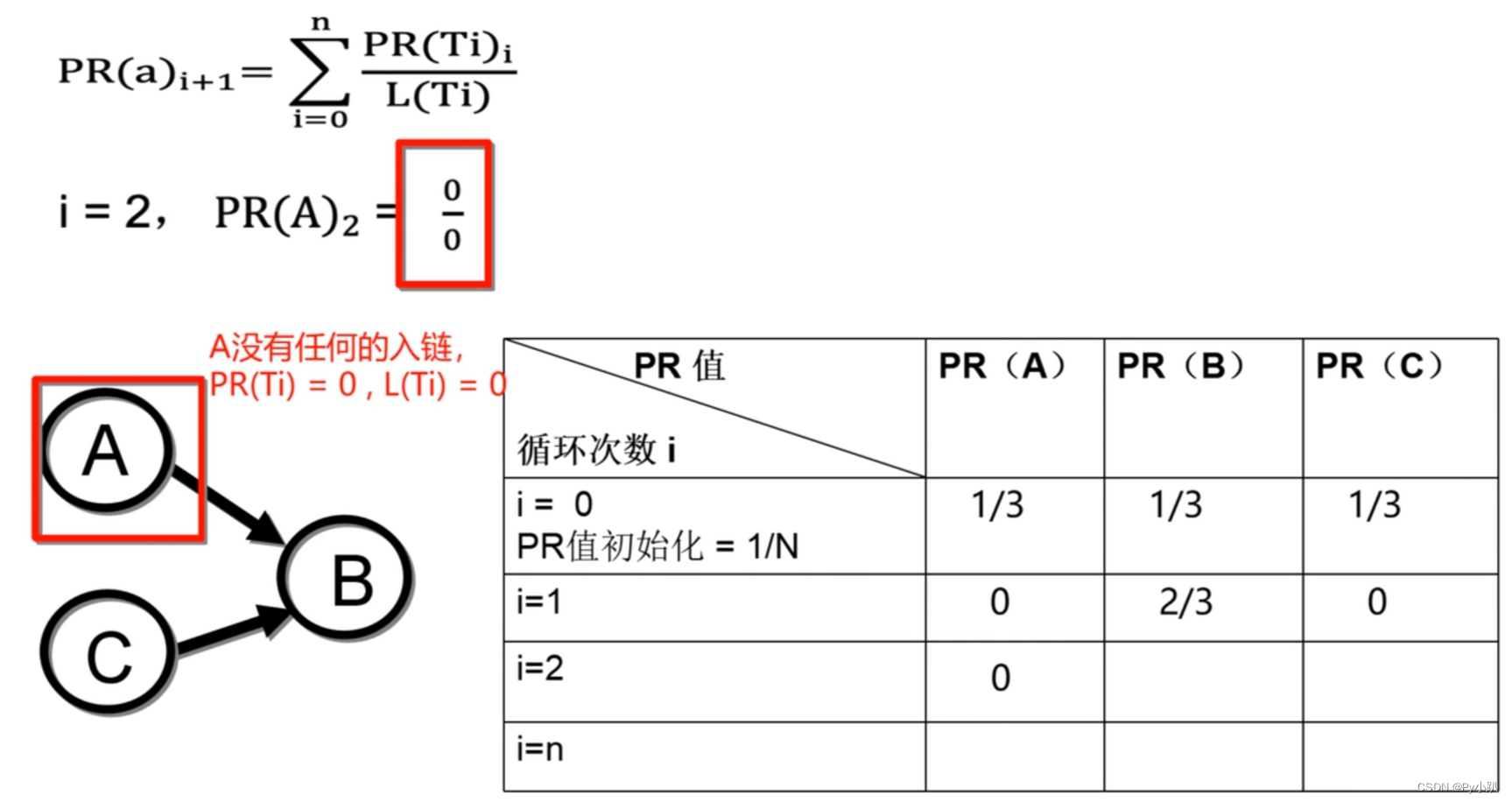



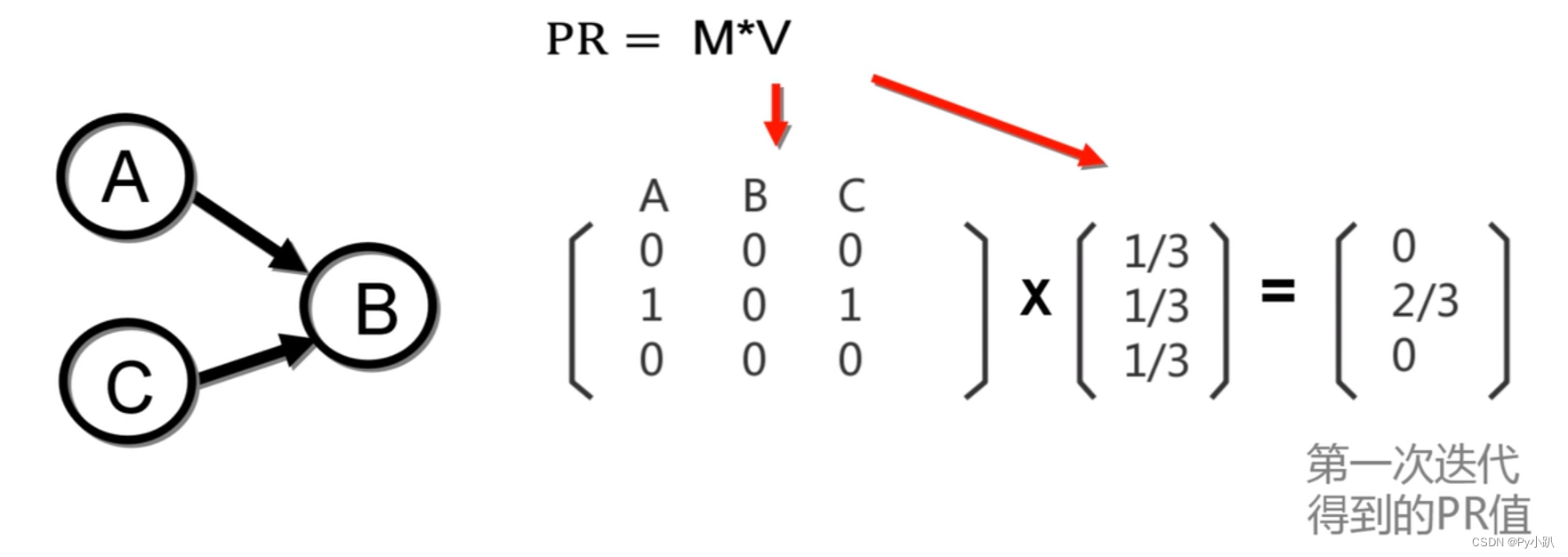
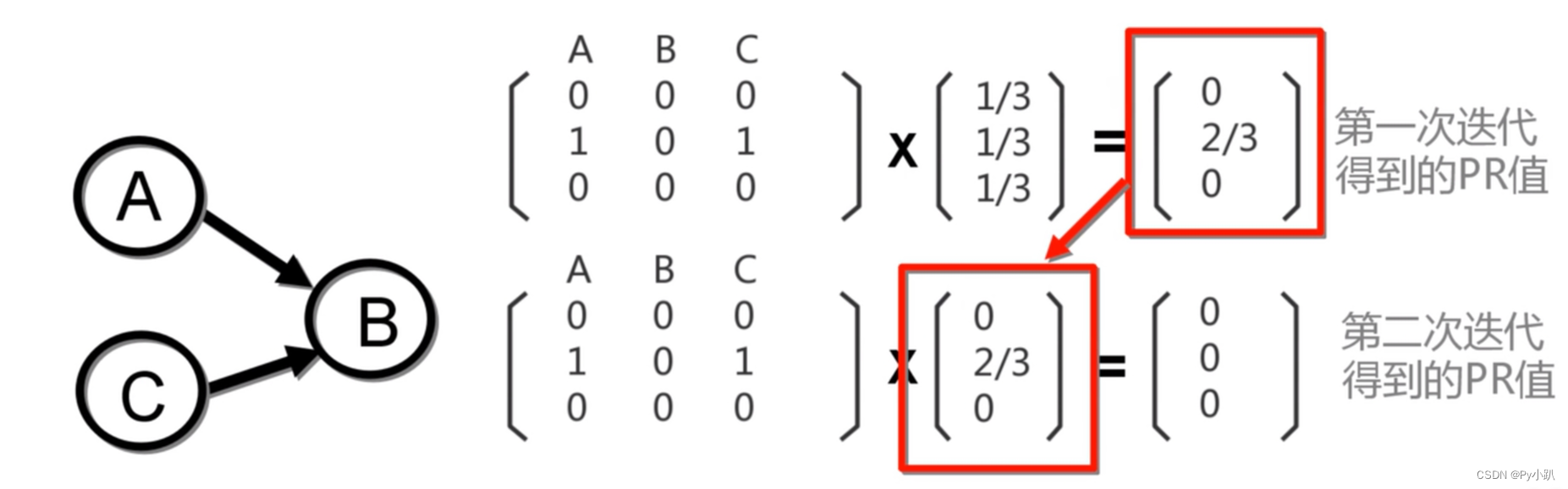
使用转移概率矩阵快速计算PR值:
解决方法:Teleport


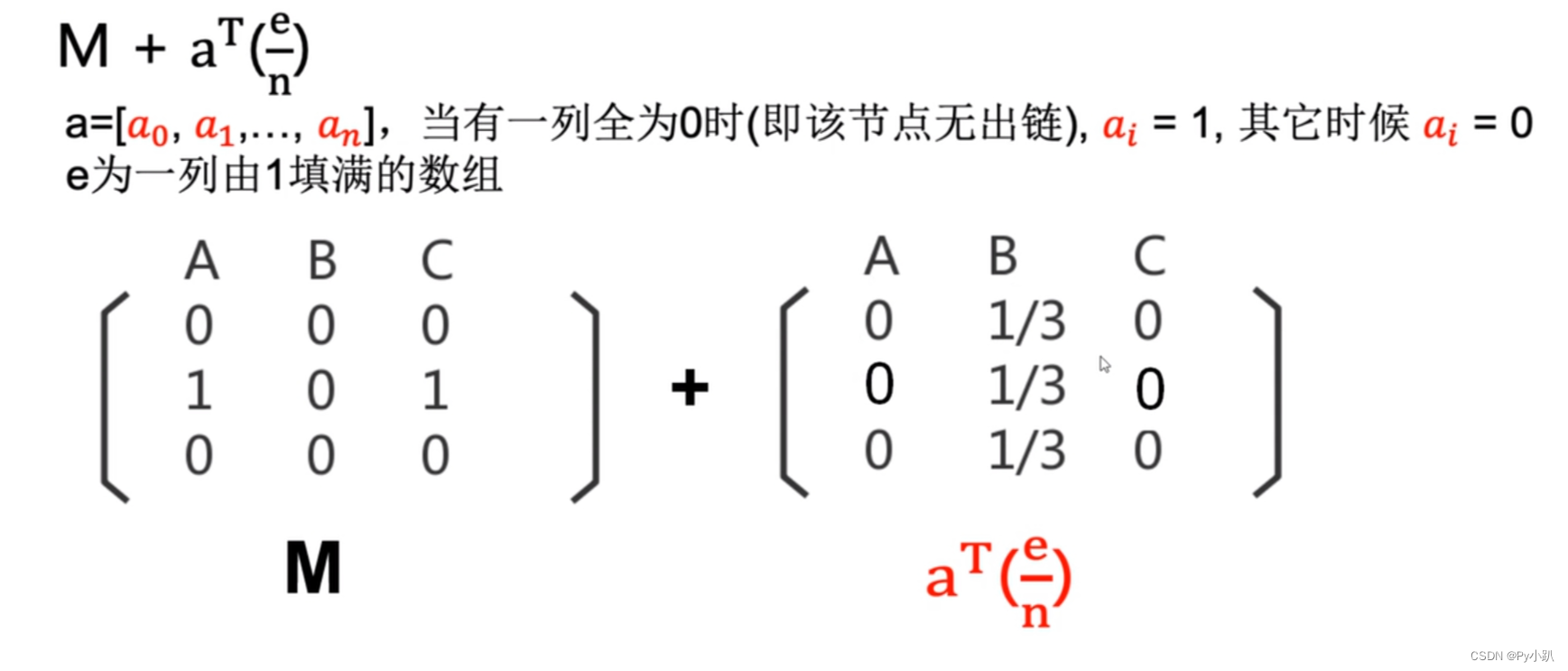
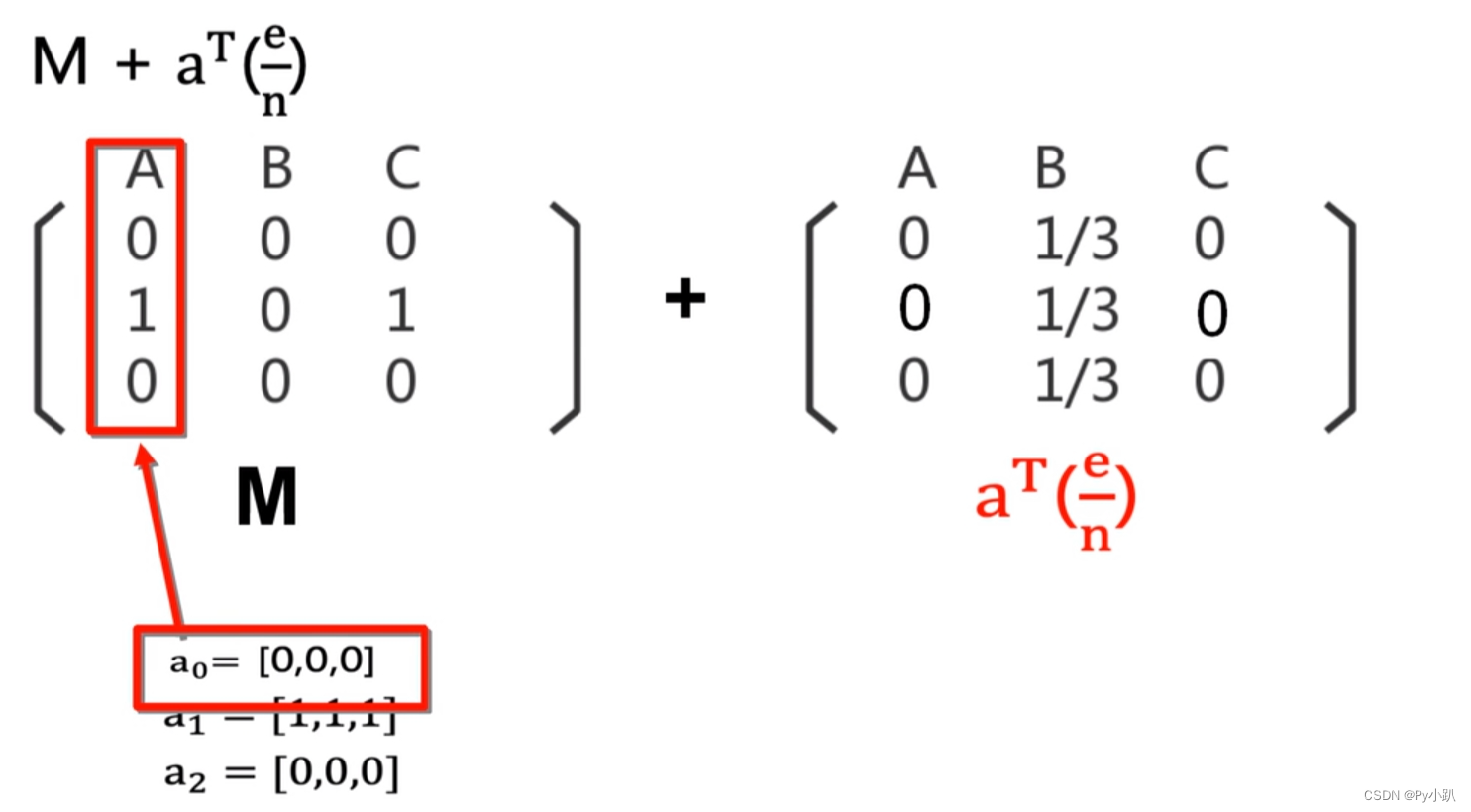
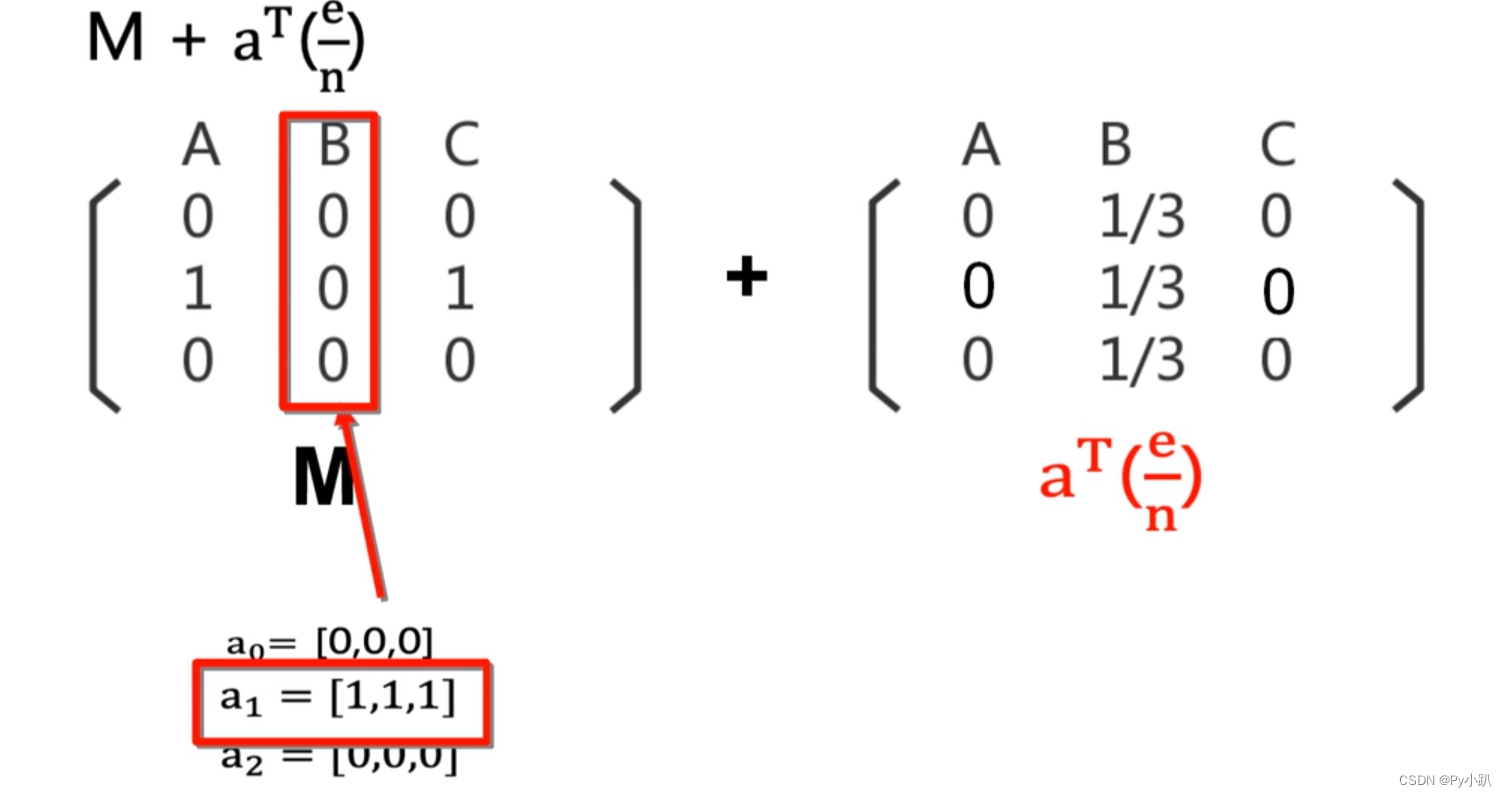
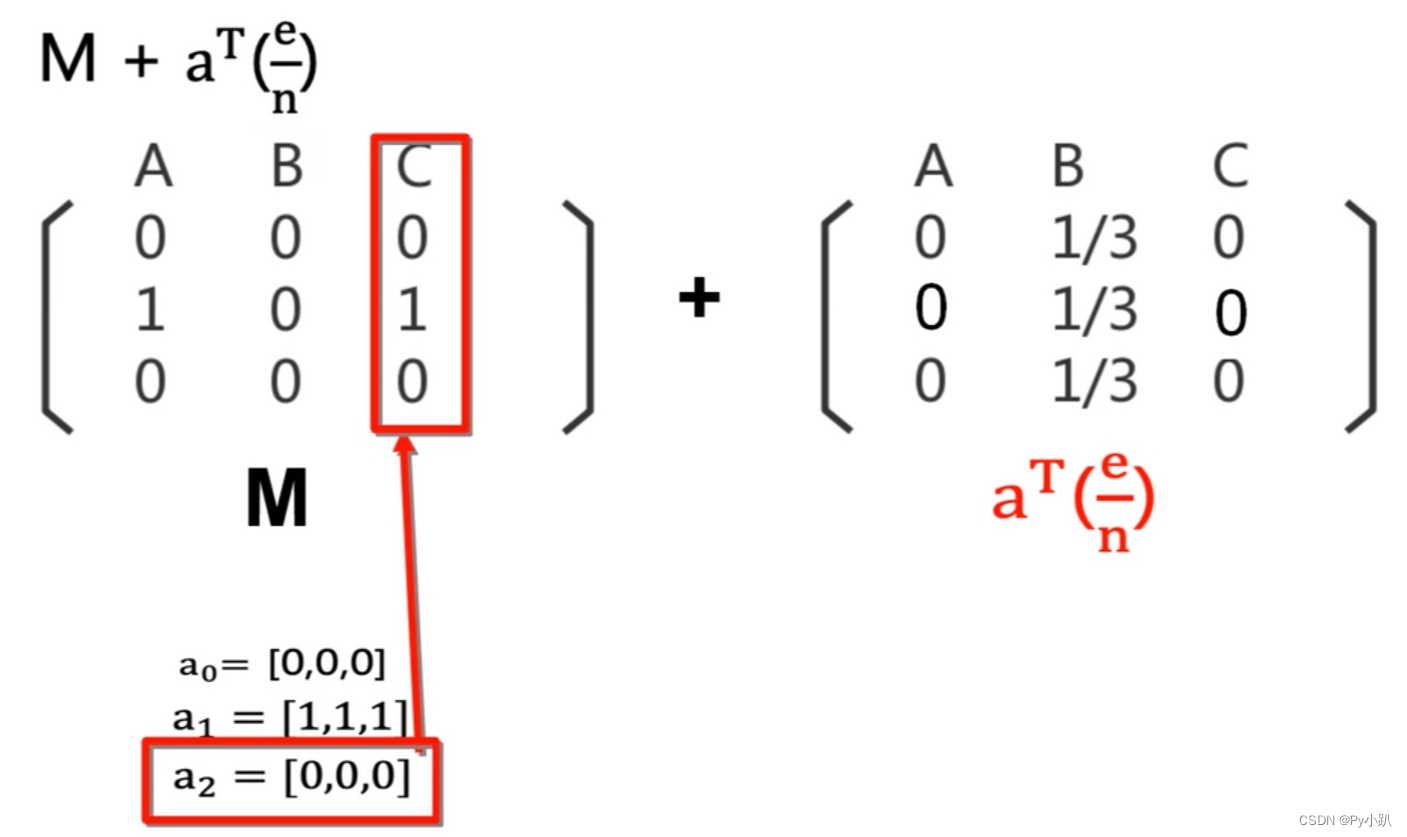

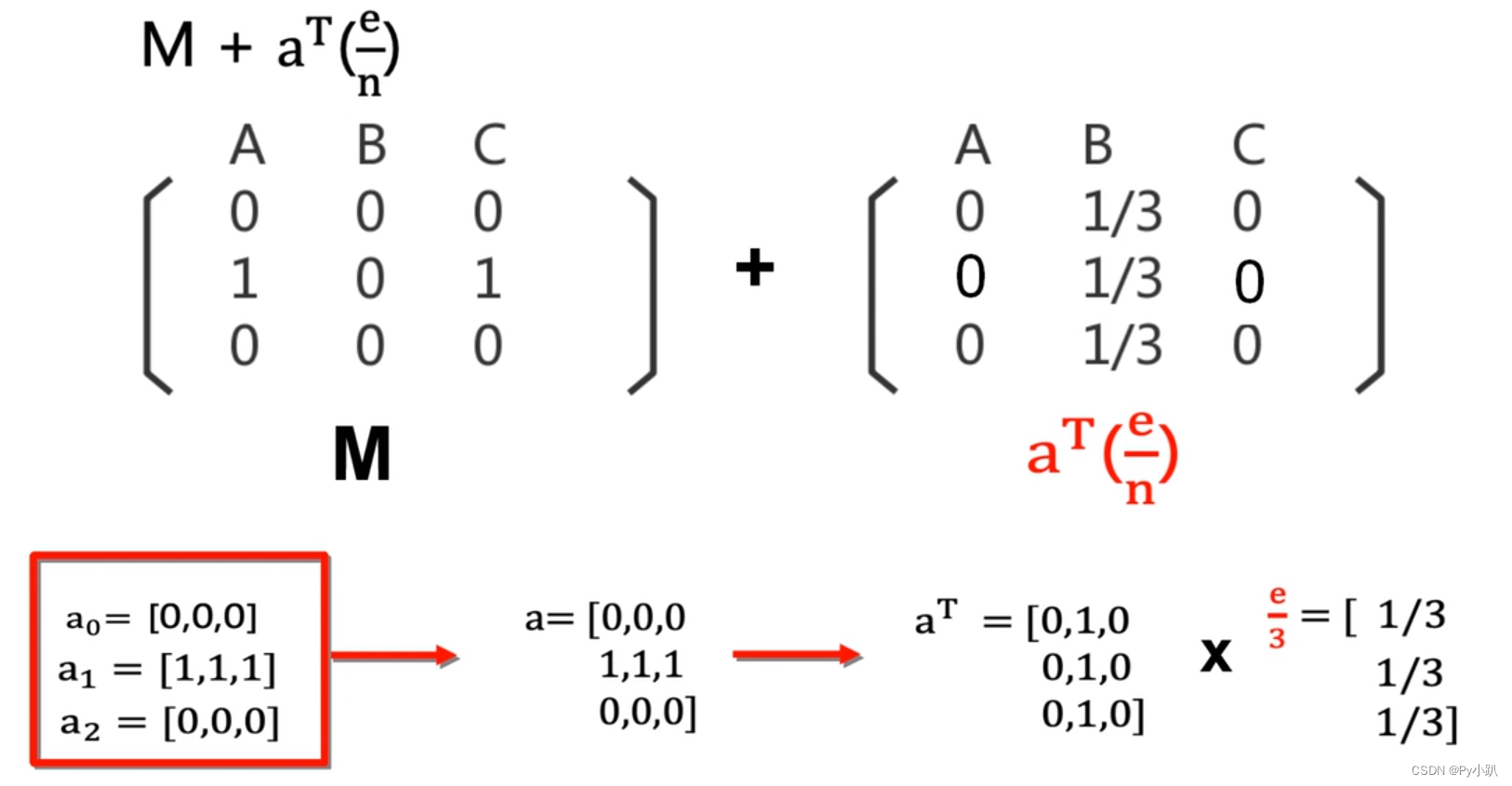
4-Dead Ends 问题修正公式

5-Spider Traps问题
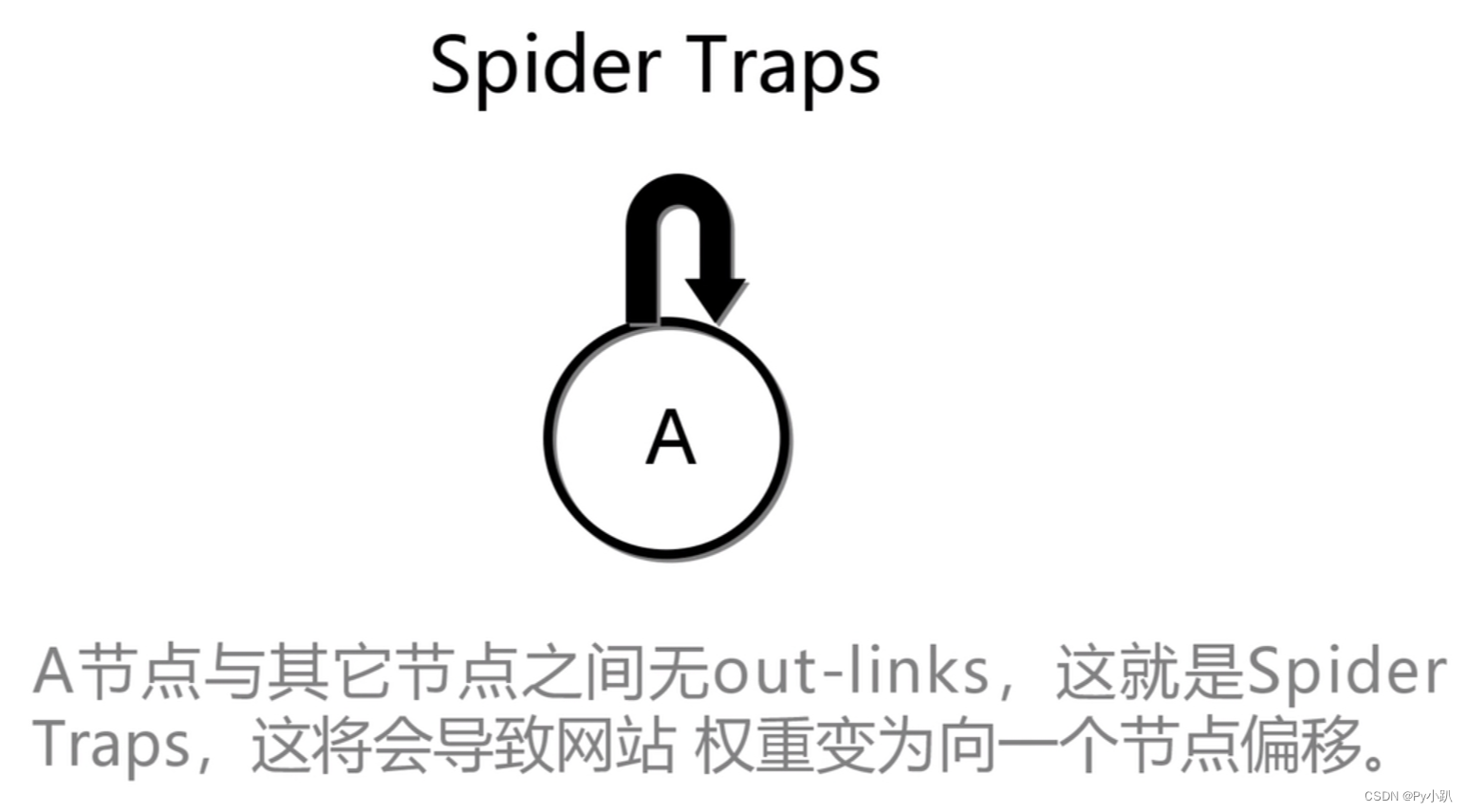



6- Spider Traps问题解决方案:Random Teleport
- 步骤1:将节点图,转换成列转移概率矩阵
- 步骤2:修正M
1转换成列转移概率矩阵

2 修正M


通常设置为0.85

第一次迭代的PR值为:
7-Spider Traps问题修正公式

8-代码案例练习[使用Jupyter Notebook编程]
import networkx as nx
import matplotlib.pyplot as plt
import random
Graph = nx.DiGraph()
Graph.add_nodes_from(range(0,100))
for i in range(100):j =random.randint(0,100)k =random.randint(0,100)Graph.add_edge(k,j)
nx.draw(Graph,with_labels=True)
plt.show()
pr = nx.pagerank(Graph,max_iter=100,alpha =0.01)
print(pr)输出结果:
{0: 0.009843202124104186, 1: 0.009843202124104186, 2: 0.009941633650425134, 3: 0.009974526667449609, 4: 0.009892665412017136, 5: 0.009843202124104186, 6: 0.009843202124104186, 7: 0.009843202124104186, 8: 0.009892665412017136, 9: 0.00997535174995786, 10: 0.009843202124104186, 11: 0.00989258290376631, 12: 0.009941633650425134, 13: 0.00989241788726466, 14: 0.009941633650425134, 15: 0.010024237480115035, 16: 0.009843202124104186, 17: 0.010041880358264236, 18: 0.009941963683428435, 19: 0.009843202124104186, 20: 0.00989291293676961, 21: 0.009843202124104186, 22: 0.009867810005684423, 23: 0.00989241788726466, 24: 0.009843202124104186, 25: 0.009975475512334098, 26: 0.00989258290376631, 27: 0.009941633650425134, 28: 0.00989291293676961, 29: 0.009868057530436899, 30: 0.010041385308759285, 31: 0.009843202124104186, 32: 0.009982839305644121, 33: 0.009843202124104186, 34: 0.009843202124104186, 35: 0.010041220292257635, 36: 0.00994188117517761, 37: 0.009876342665881136, 38: 0.00989258290376631, 39: 0.00987642517413196, 40: 0.009942004937553848, 41: 0.009843202124104186, 42: 0.00989241788726466, 43: 0.009909263185655886, 44: 0.009991096938338084, 45: 0.009892665412017136, 46: 0.009992293307975048, 47: 0.009942128699930086, 48: 0.009942128699930086, 49: 0.009843202124104186, 50: 0.00989241788726466, 51: 0.009868057530436899, 52: 0.009843202124104186, 53: 0.009867810005684423, 54: 0.009843202124104186, 55: 0.009843202124104186, 56: 0.009876342665881136, 57: 0.009941633650425134, 58: 0.009941963683428435, 59: 0.009843202124104186, 60: 0.009843202124104186, 61: 0.009843202124104186, 62: 0.009843202124104186, 63: 0.009843202124104186, 64: 0.009974774192202085, 65: 0.00989291293676961, 66: 0.009843202124104186, 67: 0.009942623749435036, 68: 0.00989241788726466, 69: 0.009843202124104186, 70: 0.009892665412017136, 71: 0.009843202124104186, 72: 0.009843202124104186, 73: 0.00999200452909716, 74: 0.009876672698884436, 75: 0.009876122643878936, 76: 0.009867810005684423, 77: 0.009941633650425134, 78: 0.009941633650425134, 79: 0.010041674087637172, 80: 0.009941633650425134, 81: 0.009843202124104186, 82: 0.009876342665881136, 83: 0.009991591987843034, 84: 0.009942128699930086, 85: 0.00987642517413196, 86: 0.00997551676645951, 87: 0.009843202124104186, 88: 0.009876672698884436, 89: 0.00987609514112866, 90: 0.009893407986274562, 91: 0.00989258290376631, 92: 0.009966489056757847, 93: 0.009876672698884436, 94: 0.00987609514112866, 95: 0.009843202124104186, 96: 0.00994188117517761, 97: 0.009942293716431735, 98: 0.00999200452909716, 99: 0.009843202124104186, 100: 0.009868057530436899}
max(pr.values())输出结果:
0.010041880358264236
import operator
max(pr.items(),key=operator.itemgetter(1))[0]输出结果:
17
sum(pr.values())输出结果:
0.9999999999999996
min(pr.values())输出结果:
0.009843202124104186
9-PageRank的优缺点
优点:
- 通过网页之间的链接来决定网页重要性,一定程度消除了认为对排名结果的影响

- 离线计算PageRank值,而非查找的时候计算,提升了查询的效率
缺点 :
- 存在时间久的网站,PageRank值会越来越大,而新生的网站,PageRank值增长慢

- 非查询相关的特性,查询结果会偏离搜索的内容
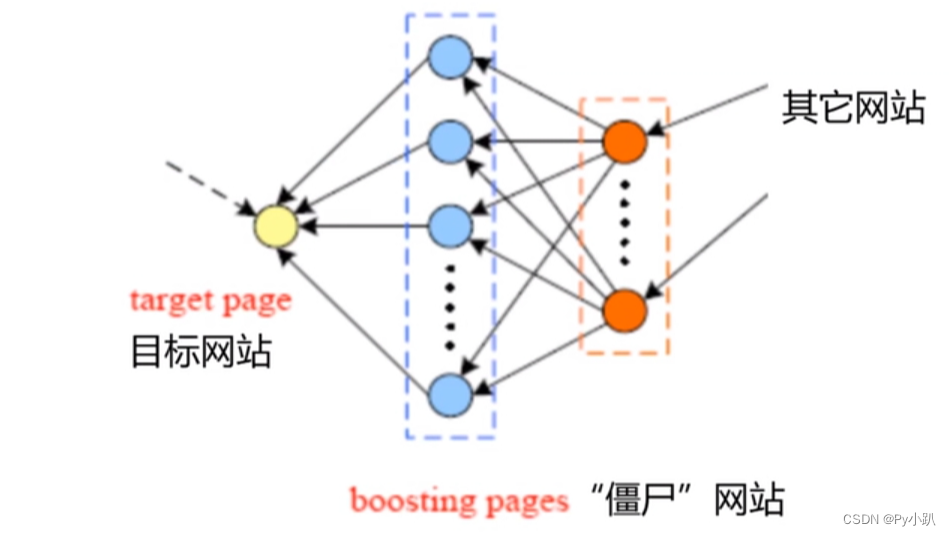
- 通过“僵尸”网站或链接,人为刷PageRank值
参考:
1.Up主帅器学习/林木的视频。
这篇关于Python数学建模学习-PageRank算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




