数模初见数建

本文主要是介绍数模初见数建，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

初见数学建模
- 1.1 数学建模是什么
- 1.2 数学建模的概述
- 1.3 如何学习数学建模---分模块化
- 1.4 数学建模前提了解
- 1.5 数学建模的六个步骤
- 1.6 如何备战建模比赛
- 1.7 数学建模赛题类型
- 1.8 数学建模算法体系概述

初见数学建模

1.1 数学建模是什么

1.原型与模型

原型：archetype（原始的模型）
- 人们在现实世界里关心、研究或从事生产、管理的实际对象；
- 特指文学艺术作品中塑造人物形象所依据的现实生活中的人；
- 指在解决问题时，对于新假设的提出有启发作用的那些事物。
模型：model
- 模型是指为了某个特定目的将原型的某一部分信息简缩、提炼构造的原型替代物，是对所研究的系统、过程、事物或概念的一种表达形式，也可指根据实验、图样放大或缩小而制作的样品，般用于展览或实验或铸造机器零件等用的模子。

2.模型的分类：

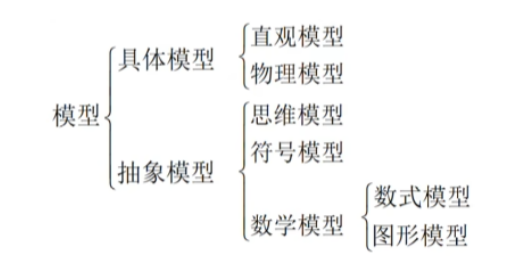
3.数学建模是什么？

数学建模是利用数学方法解决种实践。即通过抽象、简化、量等处理过程后，将实际问题达，建立起数学模型，然后运方法及计算机技术进行求解。数学模型的这个过程就称为数学建模。

4.数学模型的分类

按所用的数学知识分类:
初等模型、几何模型、微积分模型、微分方程模型、图论模型、概率统计模型、规划论模型等。
按所解决的问题的领域分类:
- 物理模型:自然科学领域内的问题；
- 非物理模型:经济模型、交通模型、人口模型、生态模型、环境模型、医学模型、社会学模型。
按所建模目的分类:
描述模型、分析模型、预报模型、优化模型、决策模型、控制模型等。
按所模型的表现特性分类:
·确定模型、随机模型;静态模型、动态模型、离散模型、连续模型。

5.数学建模到底是什么?

请为我预测一下明天的气温?（环境类）
请帮我分析一下理财产品的最优组合(财经类)
请帮我评价一下这项政策的优缺点(实证类)
请帮我对北京市的土地利用情况进行合理的划分(城市规划类)
请帮我预测一下小麦的产量(农业类)
请帮我找出标枪运动员最佳的投掷点(力学类)
等等……几乎所有的行业都要用到数学建模!很多事情无法直接凭借主观经验获取 !需要用科学的方法进行解算，此过程便是数学建模。

1.2 数学建模的概述

1.数学建模的一般步骤：

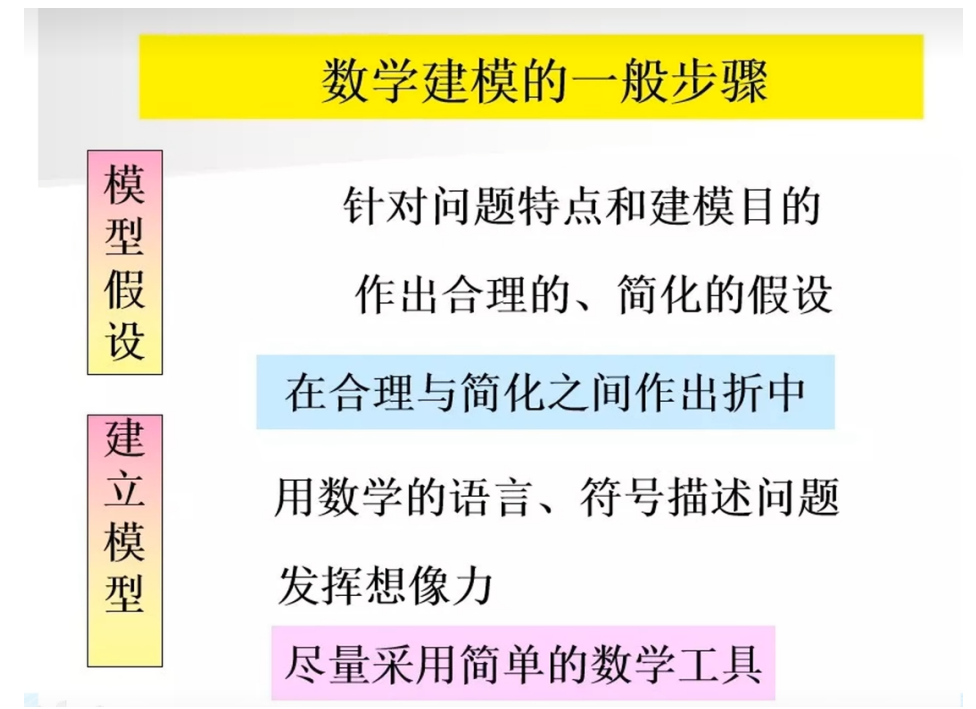
2.数学建模的全过程：

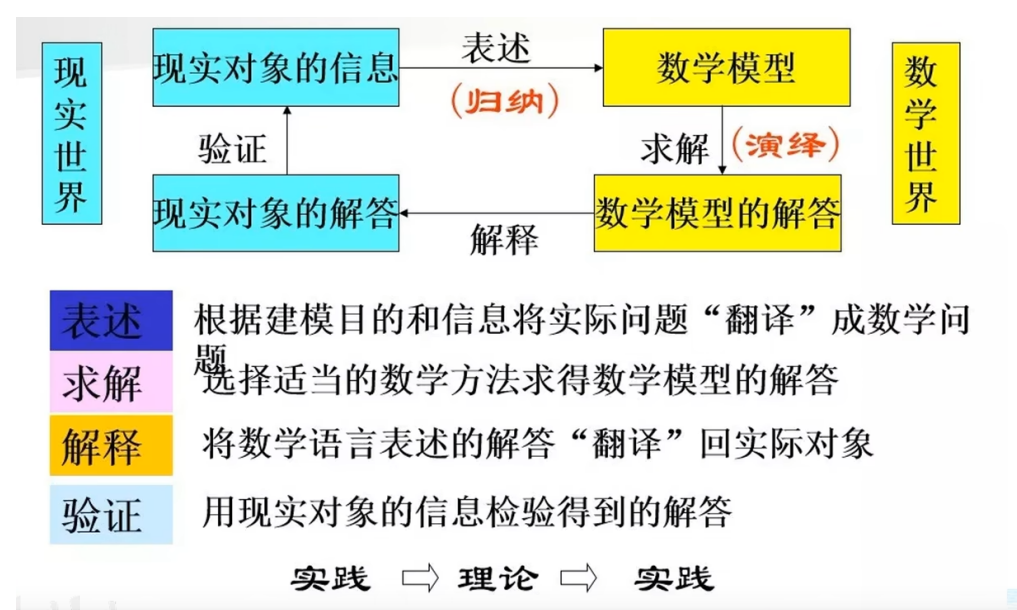
3.数学建模论文的模块：

题目：点睛之笔；
摘要、关键词：获奖关键；
问题重述：用自己的理解语言将题目中的问题反观成一个用数学语言表述的问题；
问题假设：能提高模型的准确率；
问题分析：你对问题的看法，解题的思路；
符号说明：对文章中所用符号的意义说明；
模型建立：通过一些数学符号或公式建立模型；
模型求解：用计算机语言、matlab……求解模型；
模型优缺点评价：分析这个模型的优点与不足；
参考文献。

1.3 如何学习数学建模—分模块化

1.题目备战：掌握固定模式即可。

基于_____模型的______研究与分析。

2.摘要备战：总结归纳能力，通过看高水平论文或优秀论文掌握（不要超过页面的四分之三）。

3.问题重述：切记不要直接抄袭问题，对描述剪短的拆建，描述复杂的精炼。

4.问题假设：明确假设点是关键，只要对我们的结果有影响，但又是小概率事件；或者对结果有影响，但难以计算获取这类的。

5.问题分析：动脑能力是关键，先将问题进行定性，然后说明如何求解这类问题。

6.符号说明：文中出现的符号均需说清楚，用希腊字母。

7.模型建立：将常见模型进行归纳整理，形成算法库，比赛可以直接调用。

8.模型求解：对编程语言熟练掌握，如matlab，lingo等。

9.模型优缺点评价：对模型的不足提前掌握，并在应用中的不足阐述。

10.参考文献：掌握标准格式。

1.4 数学建模前提了解

1.必须找好两个靠谱的队友，定期组织研讨和交流；

2.固定几天就看一篇优秀的数模论文，重点看摘要和问题分析以及建模过程；

3.明确分工，确保写作/建模/编程团队都具备；

4.清晰的明白建模各部分到底应该写什么；

5.对所有常见的算法进行系统的学习，明确算法用途和实现过程；

6.可以按照算法、编程、写作、排版的顺序进行。

1.5 数学建模的六个步骤

数学建模通常分为六个步骤，用数学建模解决实际问题。

1.模型准备：

了解问题的实际背景，明确其实际意义，掌握对象的各种信息。以数学思路来解释问题的精髓，数学思路贯穿问题的全过程，进而用数学语言来描述问题。要求符合数学理论，符合数学习惯，清晰准确。理解实际问题后，搜集资料，快速阅读和理解参考文献。
大白话：找对象之前先大厅对方有没有男朋友，喜欢的男生类型，了解对方的喜好。

2.问题假设：

根据实际对象的特征和建模的目的，对问题进行必要的简化，并用精确的语言提出一些恰当的假设。对涉及到的变量、变量的单位、相关假设进行定义，用表达式将其表达出来。
大白话：假设她喜欢看电影，假设她不能吃辣。

3.模型建立：

在假设的基础上，利用适当的数学工具来刻划各变量常量之间的数学关系，建立相应的数学结构。选择建模方法，由题目得到的关系式，将目标转化为某一变量的函数。
大白话：找对象要学会浪漫，可以根据她的喜好安排约会去、请客吃饭、看电影等等。

4.模型求解：

利用获取的数据资料，对模型的所有参数做出计算(或近似计算)。推导模型的公式，将数学表达式变形为建模方法的标准形式，通过限制条件，对这个型进行求解。此时可以编程用数学软件进行计算。
大白话：做了这么多要找个合适的机会向她表白，表明自己的心意。

5.模型分析：

对所要建立模型的思路进行阐述，对所得的结果进行数学上的分析。包括误差分析、数据稳定分析等等。
大白话：被拒绝是很正常的事情，反思一下自己哪里做的不够好，继续改进继续努力。

6.模型检验：

用非技术性的语言回答实际问题。将模型分析结果与实际情形进行比较，以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合，则要对计算结果给出其实际含义，并进行解释。如果模型与实际吻合较差，则应该修改假设，再次重复建过程。
大白话：将自己追对象的经历和朋友做分享，听取别人的意见，看看自己是不是舔狗。

1.6 如何备战建模比赛

分工协作及对应要求：

1.建模员：需要系统掌握各类模型，做到：

该模型的主要功能是什么？
该模型的适用场景是什么？
实现该模型需要哪些条件？
模型有哪些缺点或不足，可以做出哪些改进？

2.程序员：需要掌握matlab/python，做到：

能够熟练掌握编程基础；
能够实现各类常见算法；
能够对程序Bug做出改正；
能够熟练利用编程或软件制作精美图片（Visio）。

3.写作员：需要熟练撰写论文各模块内容：

能够掌握学术语言规范；
明白论文各模块写作要求；
能够对论文进行排版；
若撰写英文论文，需要能翻译并检查论文错误。

4.学习顺序：

建模员：学习基础知识 $\rightarrow$ 学习算法知识 $\rightarrow$ 学习优秀论文
程序员：学习编程知识 $\rightarrow$ 调试常用模型 $\rightarrow$ 复现优秀论文
写作员：掌握写作要求 $\rightarrow$ 掌握学术语言 $\rightarrow$ 掌握排版技巧
组合起来进行模拟训练。

1.7 数学建模赛题类型

1.预测类：

指通过分析已有的数据或者现象，找出其内在发展规律，然后对未来情形做出预测的过程
根据已知条件和求解目的，往往将预测类问题分为:
- 小样本内部预测；
- 大样本内部预测；
- 小样本未来预测；
- 大样本随机因素或周期特征的未来预测；
- 大样本的未来预测。
解决预测类赛题的一般步骤：
- 确定预测目标；
- 收集、分析资料；
- 选择合适的预测方法进行预测；
- 分析评价预测方法及其结果；
- 修正预测结果；
- 给出预测结果。
常见的预测方法：
- 插值与拟合方法：适合小样本内部预测；
- 回归分析法：适合中、大样本内部预测；
- 灰色预测方法：适合小样本的未来预测（有固定趋势）；
- 时间序列方法：适合中、大样本的随机因素或周期特征的未来趋势未来预测；
- 神经网络方法：适合大（特大）样本未来预测。

2.评价类：

指按照一定的标准对事物的发展或者现状进行划分的过程在数学建模中题点可体现在对生态环境社会建设，方案策略等进行评价。评价类赛题往往没有明确的指标体系和评价标准，往往是需要查阅各类资料进行构建的，因此评价类赛题也没有明确的答案。
赛题分析:解决评价类赛题的关键是指标体系的构建，构建完评价体系后在选择合适的评价方法即可，体系建立应秉承全面，准确，独立的三要素。
解决评价类赛题的一般步骤：
- 明确评价目的；
- 确定被评价的对象；
- 建立评价指标体系；
- 确定各指标相对应的权重系数；
- 选择湖构造综合评价模型；
- 计算各系统的综合评价值；
- 给出综合评价结果。
- ……
常见评价算法：
- 算术平均法；
- 几何平均法；
- 特征值法。
- ……

3.机理分析类（国赛、美赛热门，需要较大知识储备）：

所谓机理分析是根据对现实对象特性的认识，分析其因果关系，找出反映内部机理的规律。在求解机理分析类问题时首先需要探寻与问题相关的物理，化学，经济等相关的知识，然后通过对已知数据或现象的分析对事物的内在规律做出必要的假设，最后通过构建合适的方程或关系式对其内在规律进行数值表达。
赛题分析:机理分析立足于建立事物内部的规律，相对于其他类型的赛题均有章可循，机理分析类赛题往往需要结合众多关联知识才可以进行求解，如空气动力学，流体力学，热力学等。

4.优化类（国赛常客）：

指在现有现有条件固定的情况下，如何使目标效果达到最佳。如在一座城市公交车公司拥有的公交车数量是固定的，问如何安排线路能够使盈利达到最高。
优化类问题往往需要分析三个关键因素:目标函数，决策变量和约束条件，三者往往缺一不可。
赛题分析:解决优化类赛题必须知道优化的目的，约束的条件和所求解的关键变量，需要有较强的编程能力和赛题分析控掘能力。
解决优化类赛题的一般步骤：
- 确定优化目标；
- 确定决策变量；
- 构建目标函数；
- 根据已知条件构建约束条件；
- 选择合适的方法求解目标函数；
- 给出优化结果。