对极几何基本概念

本文主要是介绍对极几何基本概念，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

对极几何（Epipolar Geometry）描述的是两幅视图之间的内在射影关系，与外部场景无关，只依赖于摄像机内参数和这两幅试图之间的的相对姿态

什么是对极几何粗略概念
对极几何相关的一个重要约束5点共面约束
对极几何的几个相关概念
对应点的约束

1. 什么是对极几何·粗略概念

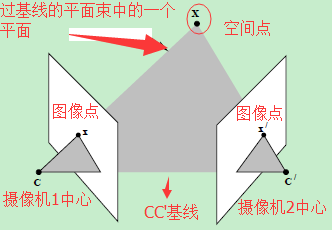
提到对极几何，一定是对二幅图像而言，对极几何实际上是“两幅图像之间的对极几何”，它是图像平面与以基线为轴的平面束的交的几何（这里的基线是指连接摄像机中心的直线），以下图为例：对极几何描述的是左右两幅图像(点x和x’对应的图像)与以CC’为轴的平面束的交的几何！

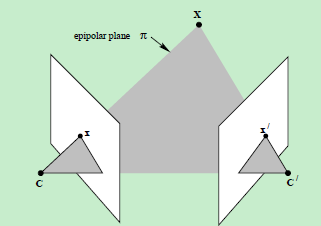
这里写图片描述

直线CC’为基线，以该基线为轴存在一个平面束，该平面束与两幅图像平面相交，下图给出了该平面束的直观形象，可以看到，该平面束中不同平面与两幅图像相交于不同直线；

上图中的灰色平面 $\pi$ ，只是过基线的平面束中的一个平面（当然，该平面才是平面束中最重要的、也是我们要研究的平面）；

2. 对极几何相关的一个重要约束·5点共面约束

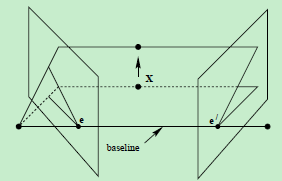
仍以上面贴出的图像为例，此处重复贴出，空间点X在两幅图像中的像分别为x和x’，这两个投影点之间存在什么关系呢？观察下图
这里写图片描述

点x、x’与摄像机中心C和C’是共面的，并且与空间点X也是空面的，这5个点共面于平面 $\pi$ ！这是一个最本质的约束，即5个点决定了一个平面 $\pi$
由该约束，可以推导出一个重要性质：由图像点x和x’反投影的射线共面，并且，在平面 $\pi$ 上，在搜索点对应中，该性质非常重要

3. 对极几何的几个相关概念

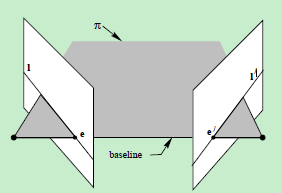
对极平面束（epipolar pencil）：以基线为轴的平面束；下图给出了包含两个平面的对极平面束
对极平面（epipolar plane）：任何包含基线的平面都称为对极平面，或者说是对极平面束中的平面；例如，下图中的平面 $\pi$ 就是一个对极平面
对极点（epipole）：摄像机的基线与每幅图像的交点；即上图中的点e和e’
对极线（epipolar line）：对极平面与图像的交线；例如，上图中的直线l和l’

4. 对应点的约束

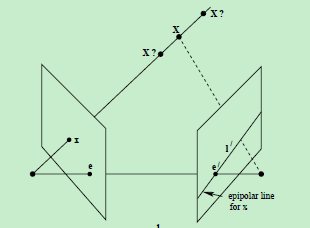
现在假设只知道图像点x，那么，它的对应点x’如何约束呢？
这里写图片描述

根据前面的讨论，点x和x’一定位于平面 $\pi$ 上，而平面 $\pi$ 可以利用基线CC’和图像点x的反投影射线确定
点x’又是右侧图像平面上的点，所以，点x’一定位于平面 $\pi$ 与右侧图像平面的交线l’上
前面提到，直线l’为点x的对极线，也就是说，点x的对应点x’一定位于它的对极线上！

Reference
[1]《计算机视觉中的多视几何》 ·第八章·对极几何和基本矩阵
[2] 《Multiple View Geometry in Computer Vision Second Edition》·Andrew Zisserman·P239·9 Epipolar Geometry and the Fundamental Matrix

这篇关于对极几何基本概念的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！