本文主要是介绍自然语言处理: 第二十三章大模型基底之Mistral 7B,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章地址: 2401.04088.pdf (arxiv.org)
项目地址: mistralai/mistral-src: Reference implementation of Mistral AI 7B v0.1 model
前言
Mistral 7B作为Mistral AI公司推出的第一个基座大模型,也有很多地方借鉴了LLaMa2的闪光点也采用了GQA(分组查询注意力) 以及RoPE(旋转位置编码)–(目前似乎是标配了)。在此基础上,为了踩在LLaMa2的肩膀上更进一步,Mistral AI 使用了SWA(滑动窗口注意力机制)进一步解决了长本文的问题,如图1所示Mistral 7B的文本长度已经达到了32K(LLaMa2只有4K).
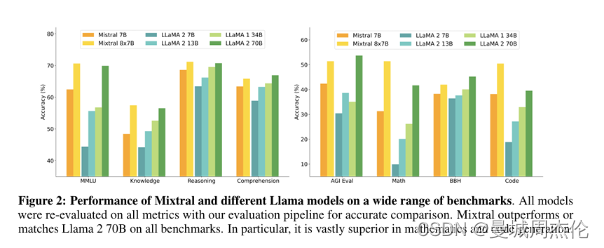
基于上面这些改进,作者将Mistral7B与LLaMa各个参数的版本进行了对比,其结果如图2所示。可以看到: Mistral 7B在所有指标上均超过了Llama 2 13B,并在大多数基准测试中优于Llama 1 34B。特别是,Mistral 7B在代码、数学和推理基准测试中表现出卓越的性能,并在不牺牲非代码基准测试性能的情况下接近Code-Llama 7B的代码性能。
### 核心一. 滑动窗口注意力SWA(slide window attention)
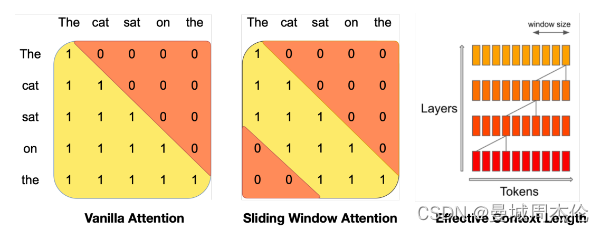
滑动窗口注意力SWA是Mistral 7B 相比于LLaMa系列最突出的创新点,其主要解决了长文本问题。熟悉attention机制的都知道,如图在计算vanilla attention的时候都会计算整个生成句子的每个token的注意力值,但是对于长文本来说大部分情况应当是离的越近会更大概率更相关, 所以理论上并不需要算所有token的注意力值。 基于此SWA就提出来了,以图4.中的例子为例:
在面对这个序列时:The cat sat on the。
如果是标准注意力,在计算最后一个token “the”时,得计算the本身所对应的query与整个上文每个token对应的key的内积即需要计算5个注意力,当序列长度一长时,该计算量还是比较大的。
但如果是滑动窗口注意力,则在计算最后一个token “the”时,只需计算the本身所对应的query与上文中N(N是窗口长度)个token对应的key的内积 。
可以看到SWA的确减少了很多运算,但是每个token只关注前面的N个token的注意力的话,精度会不会损失? 这个问题其实作者在原文中也给出了解释,如图4所示: 只要transformer层够深,即使窗口大小仅仅为4,通过这种4层的transformer结构,我同样能看到最远的4 * 4= 16tokens的长度范围。所以精度损失并不是很大。
我们知道在LLM推理时,一般分为prompting 和 generation两个阶段,为了满足SWA,prompting阶段可以通过一个mask的掩码操作实现,如下
if input_ids.shape[1] > 1:# seqlen推理时在prompt阶段为n,在generation阶段为1seqlen = input_ids.shape[1]# mask在推理时也只在prompt阶段有,#定义一个全1方阵tensor = torch.full((seqlen, seqlen),fill_value=1)# 上三角部分全为0mask = torch.tril(tensor, diagonal=0).to(h.dtype)# make the mask banded to account for sliding window# 这里代码diagonal应该等于(-self.args.sliding_window+1)才能满足window size为 # self.args.sliding_window,这应该是官方代码的一个小bug?mask = torch.triu(mask, diagonal=-self.args.sliding_window)mask = torch.log(mask)
"""
举个例子,tensor.shape : [10,10]
self.args.sliding_window = 5,则mask为
tensor([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],[1, 1, 0, 0, 0, 0, 0, 0, 0, 0],[1, 1, 1, 0, 0, 0, 0, 0, 0, 0],[1, 1, 1, 1, 0, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 1, 0, 0, 0, 0],[0, 1, 1, 1, 1, 1, 1, 0, 0, 0],[0, 0, 1, 1, 1, 1, 1, 1, 0, 0],[0, 0, 0, 1, 1, 1, 1, 1, 1, 0],[0, 0, 0, 0, 1, 1, 1, 1, 1, 1]])
"""
而在generation阶段,因为是自回归生成所以mask起不到作用,那此时mistral则使用了RotatingBufferCache来实现此操作,具体而言,就是采用一种循环右移的存储方式,剔除离得远的K,保存靠近的K 。
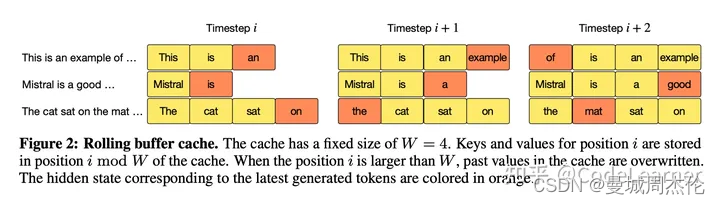
如上图展示了一个Window Size为4的Cache,循环右移的写Cache的示意图。
RotatingBufferCache代码实现如下
# The cache is a rotating buffer
# positions[-self.sliding_window:] 取最后w个位置的索引,取余
# [None, :, None, None]操作用于扩维度[1,w,1,1]
scatter_pos = (positions[-self.sliding_window:] % self.sliding_window)[None, :, None, None]
# repeat操作repeat维度 [bsz, w, kv_head, head_dim]
scatter_pos = scatter_pos.repeat(bsz, 1, self.n_kv_heads, self.args.head_dim)
# src取[:,-w,:,:] 所以src.shape=[bsz,w,kv_head,head_dim]
# 根据scatter_pos作为index 将src写入cache
self.cache_k[:bsz].scatter_(dim=1, index=scatter_pos, src=xk[:, -self.sliding_window:])
self.cache_v[:bsz].scatter_(dim=1, index=scatter_pos, src=xv[:, -self.sliding_window:])
核心二. 分组查询注意力GQA(Grouped-query attetion)
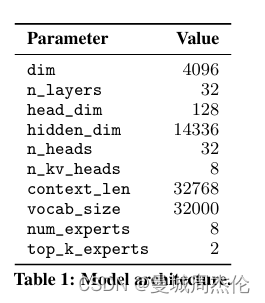
如图2所示,除了常见的一些参数之外,我们可以发现一个n_kv_heads,那么这个是啥呢?其实与LLaMa2一样,Mistral 7B 同样使用了GQA分组查询注意力。其中n_heads =32共计32个头,n_kv_heads=8,说明每组kv共享4组query。这么说好像还是有点不理解,别着急听笔者细细道来。
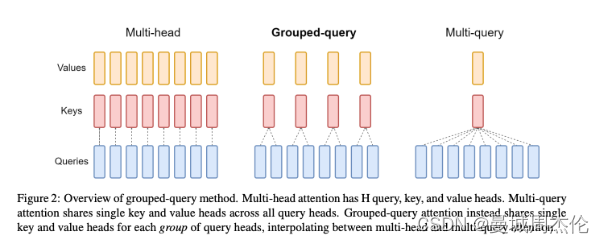
原始的 MHA(Multi-Head Attention,QKV 三部分有相同数量的头,且一一对应。每次做 Attention,head1 的 QKV 就做好自己运算就可以,输出时各个头加起来就行。而 MQA(Multi-query Attention) 则是,让 Q 仍然保持原来的头数,但 KV只有一个,相当于所有的 Q 头共享一组 K 和 V 头,所以叫做 Multi-Query 了,这是LLaMa1采用的原理。而显而易见的这样虽然会提高速度,但是由于共享KV所以精度会下降很多,从而到了LLaMa2和Mistral里,GQA 通过分组一定头数共享一组KV,从而达到性能和计算中的一个trade-off,这样既不像MQA一样降低很多精度,也可以相比于NHA提高速度。(有关于GQA的具体细节可以参考上一篇文章:自然语言处理: 第二十一章大模型基底之llama2 )
前文的谜底揭晓:说明在Mistral 的GQA中,一组KV共享4组Q。
核心三. RoPE(旋转位置编码)
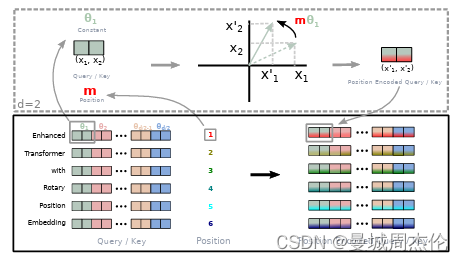
最后同样的,Mistral也同样配备了RoPE旋转位置编码–其核心思想是“通过绝对位置编码的方式实现相对位置编码”,这一构思具备了绝对位置编码的方便性,同时可以表示不同 token 之间的相对位置关系。如图6是RoPE旋转位置编码的机理图解,不同于原始 Transformers 中将 pos embedding 和 token embedding 进行相加,RoPE 是将位置编码和 query (或者 key) 进行相乘。
具体来说,在对序列进行位置编码时和标准Transformer不同,LlaMa 的位置编码在每个Attention层中分别对Q K 进行RoPE位置编码,而不是在Transformer Block之前进行一次位置编码,也就是说每次计算Attention时都分别要对Q和 K做位置编码。
这篇关于自然语言处理: 第二十三章大模型基底之Mistral 7B的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



