代码随想录算法训练营第二十三天| 669.修建二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树

本文主要是介绍代码随想录算法训练营第二十三天| 669.修建二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

系列文章目录

---

---

669. 修剪二叉搜索树

①递归法

注：不能在遇到 root.val < low || root.val > high 的时候直接return null，因为下图所示：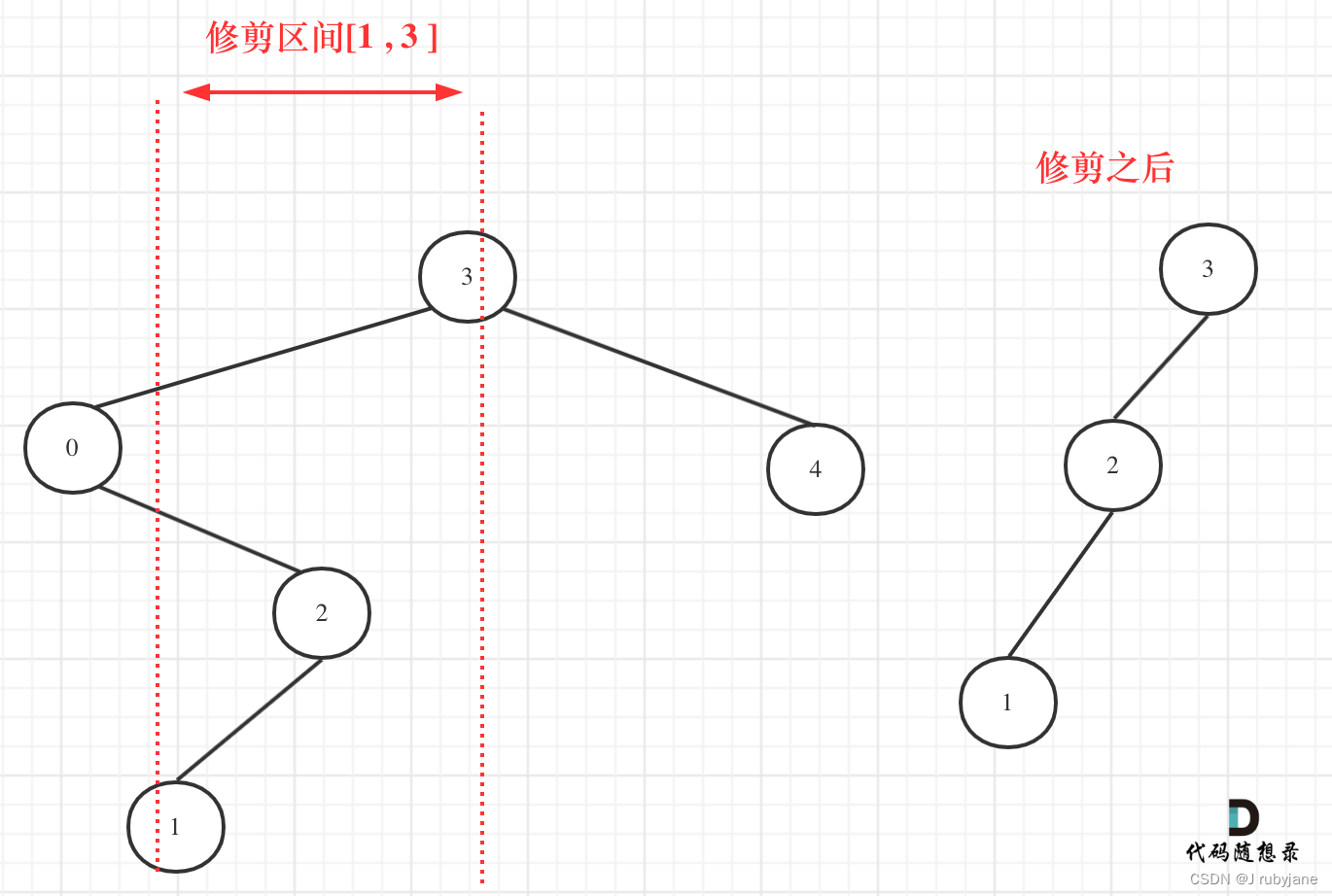
[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的，还要考虑节点0的右子树。节点0并不符合区间要求，那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了（就是把节点0从二叉树中移除），如下图所示：

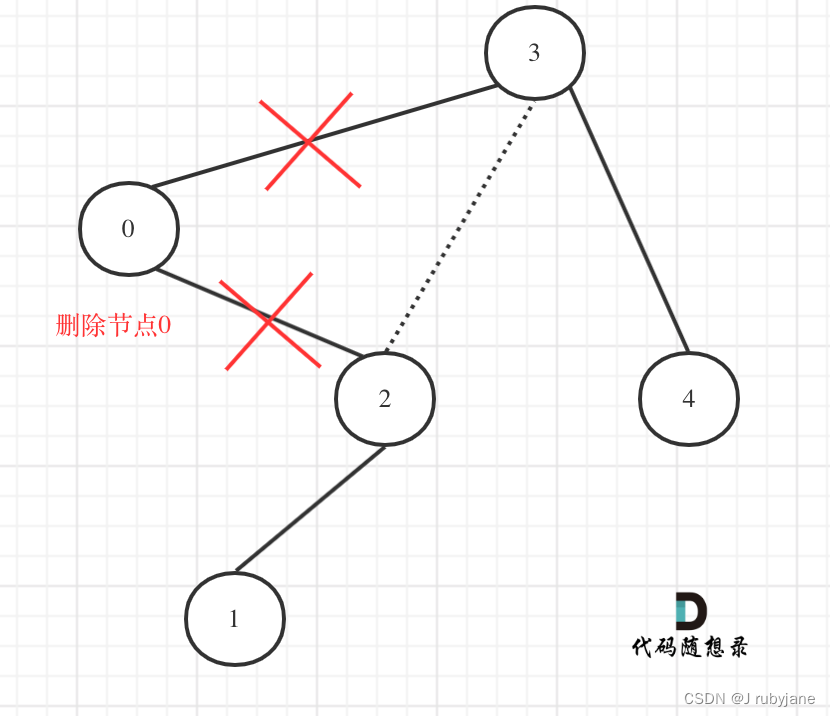
class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {//确定终止条件if (root == null) return null;//确定单层递归的逻辑//中//如果root（当前节点）的元素小于low的数值，那么应该递归右子树，并返回右子树符合条件的头结点。if (root.val < low) {return trimBST(root.right, low, high);}//如果root(当前节点)的元素大于high的，那么应该递归左子树，并返回左子树符合条件的头结点。if (root.val > high) {return trimBST(root.left, low, high);}root.left = trimBST(root.left, low, high);//左 接入符合条件的左子树root.right = trimBST(root.right, low, high);//右 接入符合条件的右子树return root;}
}

②迭代法（不好想出，掌握递归即可）

1. 因为二叉搜索树的有序性，不需要使用栈模拟递归的过程。
2. 在剪枝的时候，可以分为三步：
   • 将root移动到[L, R] 范围内，注意是左闭右闭区间；
   • 剪枝左子树；
   • 剪枝右子树；

class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if (root == null) return null;//中 确定最后要返回的根节点while (root != null && (root.val < low || root.val > high)) {if (root.val < low) {root = root.right;} else {root = root.left;}}//在根节点一定在区间内的前提下，剪枝//左、对左子树剪枝，左子树的所有节点都小于high，只需要判断是否小于lowTreeNode curr = root;while (curr != null) {// 如果左节点的值小于low，证明左节点以及左节点的左子树都小于low，要剪掉，继续判断左节点的右子树即可while (curr.left != null && curr.left.val < low) {curr.left = curr.left.right;}// 现在的左节点大于等于low，则继续往左遍历curr = curr.left;}//右 对右子树剪枝，右子树的所有节点都大于low，只需要判断节点是否大于highcurr = root;// 如果右节点的值大于high，证明右节点以及右节点的的右子树都大于high，要剪掉，继续判断右节点的左子树即可while (curr != null) {while (curr.right != null && curr.right.val > high) {curr.right = curr.right.left;}// 现在的右节点小于等于high，则继续往右遍历curr = curr.right;}return root;}
}

---

108.将有序数组转换为二叉搜索树

本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间。分割点就是数组中间位置的节点。如果数组长度为偶数，中间节点有两个，取哪一个都可以，只不过构成了不同的平衡二叉搜索树。

递归法

注：

1.在构造二叉树的时候尽量不要重新定义左右区间数组，而是用下标来操作原数组。
2.取数组中间元素的位置，不难写出int mid = (left + right) / 2;，这么写其实有一个问题，就是数值越界，例如left和right都是最大int，这么操作就越界了，尤其需要注意！所以可以这么写：int mid = left + ((right - left) / 2);。

[左闭右开)

class Solution {public TreeNode sortedArrayToBST(int[] nums) {return makeBST(nums, 0, nums.length);}//左闭右开public TreeNode makeBST(int[] nums, int begin, int end) {//终止条件if (begin >= end) return null;//单层循环逻辑// 构建平衡二叉树的关键是选中间/靠近的节点作为根节点int index = begin + (end - begin) / 2;//中节点索引int rootVal = nums[index];TreeNode root = new TreeNode(rootVal);//构造根节点// 构建左右子树root.left = makeBST(nums, begin, index);root.right = makeBST(nums, index + 1, end);return root;}
}

[左闭右闭]

class Solution {public TreeNode sortedArrayToBST(int[] nums) {return makeBST(nums, 0, nums.length - 1);}public TreeNode makeBST(int[] nums, int begin, int end) {//终止条件if (begin > end) return null;//单层循环逻辑int index = begin + (end - begin) / 2;int rootVal = nums[index];TreeNode root = new TreeNode(rootVal);//创建根节点root.left = makeBST(nums, begin, index - 1);root.right = makeBST(nums, index + 1, end);return root;}
}

---

538.把二叉搜索树转换为累加树

这是一棵树，换一个角度来看，这就是一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]。从树中可以看出累加的顺序是右中左，所以我们需要反中序遍历这个二叉树，然后顺序累加就可以了。本题依然需要一个pre指针记录当前遍历节点cur的前一个节点，这样才方便做累加。

①递归法-反中序遍历（右中左）+双指针

class Solution {TreeNode pre = null;int value = 0;public TreeNode convertBST(TreeNode root) {if (root == null) return null;root.right = convertBST(root.right);//右if (pre != null) {//中root.val += pre.val;}pre = root;root.left = convertBST(root.left);//左return root;}
}

②迭代法-反中序遍历（右中左）+双指针

统一迭代法

class Solution {public TreeNode convertBST(TreeNode root) {if (root == null) return null;Stack<TreeNode> st = new Stack<TreeNode>();st.push(root);TreeNode pre = null;while (!st.isEmpty()) {TreeNode node = st.peek();if (node != null) {st.pop();if (node.left != null) st.push(node.left);//左st.push(node);//中st.push(null);if (node.right != null) st.push(node.right);//右} else {//中节点处理逻辑st.pop();node = st.pop();if (pre != null) {node.val += pre.val;}pre = node;}}return root;}
}

普通迭代法

class Solution {public TreeNode convertBST(TreeNode root) {if (root == null) return null;Stack<TreeNode> st = new Stack<TreeNode>();TreeNode cur = root;TreeNode pre = null;while (cur != null || !st.isEmpty()) {if (cur != null) {st.push(cur);cur = cur.right;//右} else {cur = st.pop();//中if (pre != null) {cur.val += pre.val;}pre = cur;cur = cur.left;}}return root;}
}

---

这篇关于代码随想录算法训练营第二十三天| 669.修建二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---