算法沉淀——动态规划篇（子数组系列问题（下））

本文主要是介绍算法沉淀——动态规划篇（子数组系列问题（下）），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

几乎所有的动态规划问题大致可分为以下5个步骤，后续所有问题分析都将基于此

• 1.、状态表示：通常状态表示分为以下两种，其中更是第一种为主。

  • 以i为结尾，dp[i] 表示什么，通常为代求问题（具体依题目而定）
  • 以i为开始，dp[i]表示什么，通常为代求问题（具体依题目而定）

• 2、状态转移方程

  • 以上述的dp[i]意义为根据， 通过最近一步来分析和划分问题，由此来得到一个有关dp[i]的状态转移方程。

• 3、dp表创建，初始化

  • 动态规划问题中，如果直接使用状态转移方程通常会伴随着越界访问等风险，所以一般需要初始化。而初始化最重要的两个注意事项便是：保证后续结果正确，不受初始值影响；下标的映射关系。
  • 而初始化一般分为以下两种：
    • 直接初始化开头的几个值。
    • 一维空间大小+1，下标从1开始；二维增加一行/一列。

• 4、填dp表、填表顺序：根据状态转移方程来确定填表顺序。

• 5、确定返回值

一、等差数列划分

【题目】：413. 等差数列划分
【题目】：

 如果一个数列 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该数列为等差数列。例如，[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。
 给你一个整数数组 nums ，返回数组 nums 中所有为等差数组的 子数组 个数。(子数组 是数组中的一个连续序列)

【示例】：

输入：nums = [1,2,3,4]
输出：3
解释：nums 中有三个子等差数组：[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。

【分析】：
 我们可以定义dp[i]表示以i为结尾，等差数组的子数组个数。之后我们可以通过判断（nums[i]、nums[i-1]、nums[i-2]）是否构成等差数列，来进一步分析

状态转移方程推导：

1. 如果nums[i]、nums[i-1]、nums[i-2]不构成等差数列，显然此时以i为结尾的等差数组的子数组个数为0。即dp[i] = 0;
2. 如果构成等差数列，此时dp[i]的值至少为1。此时我们还需加上dp[i-1]的值。原因在于如果以i-1为结尾的等差数列存在，此时该等差数列公差为dp[i-1] -dp[i-2]。同时nums[i]、nums[i-1]、nums[i-2]构成等差数列，公差也为dp[i-1] -dp[i-2]。这也意味着，以i-1为结尾的所有等差数列，在添加新增nums[i]元素后，依然是等差数列。所以状态转移方程为dp[i] = dp[i - 1] + 1;

细节处理：
 显然当i为1、2时，状态转移方程不适用。我们由于dp[0]、dp[1]一定构不成等差数列，所以我们可以先将dp[0]、dp[1]先初始化为0，在从下标2开始，从左往右填表。

【代码编写】：

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();vector<int> dp(n);int ret = 0;for(int i = 2; i < n; i++){if(nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2])dp[i] = dp[i - 1] + 1;ret += dp[i];//累加所有结果}return ret;}
};

二、最长湍流子数组

【题目链接】：978. 最长湍流子数组
【题目】：

 给定一个整数数组 arr ，返回 arr 的 最大湍流子数组的长度 。如果比较符号在子数组中的每个相邻元素对之间翻转，则该子数组是 湍流子数组 。
 更正式地来说，当 arr 的子数组 A[i], A[i+1], …, A[j] 满足仅满足下列条件时，我们称其为湍流子数组：
若 i <= k < j ：当 k 为奇数时， A[k] > A[k+1]，且当 k 为偶数时，A[k] < A[k+1]；
或 若 i <= k < j ：当 k 为偶数时，A[k] > A[k+1] ，且当 k 为奇数时， A[k] < A[k+1]。

【示例】：

输入：arr = [9,4,2,10,7,8,8,1,9]
输出：5
解释：arr[1] > arr[2] < arr[3] > arr[4] < arr[5]

【分析】：
 我们定义f[i]表示以i位置为结尾，并且最后是“上升”趋势的最长湍流子数组大小；g[i]表示以i位置为结尾，并且最后是“下降”趋势的最长湍流子数组大小。

状态转移方程推导：
 此时以i为结尾的湍流子数组长度可能为1，或大于1。具体如下：

特殊处理：
 以i为结尾的湍流子数组中，不管最后一步是呈上升趋势还是下降趋势，最小长度一定为1，即nums[i]本身。所以我们在创建f和g表时，可以将初始值设为1。后续填表过程中，仅需考虑子数组长度大于1的情况即可！！

【代码编写】：

class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {int n = arr.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for(int i = 1; i < n; i++){if(arr[i] > arr[i - 1])f[i] = g[i - 1] + 1;else if(arr[i] < arr[i - 1])g[i] = f[i - 1] + 1;ret = max(ret, max(f[i], g[i]));}return ret;}
};

三、单词拆分

【题目链接】：139. 单词拆分
【题目】：

 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
 注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

【示例】：

输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意，你可以重复使用字典中的单词。

【分析】：
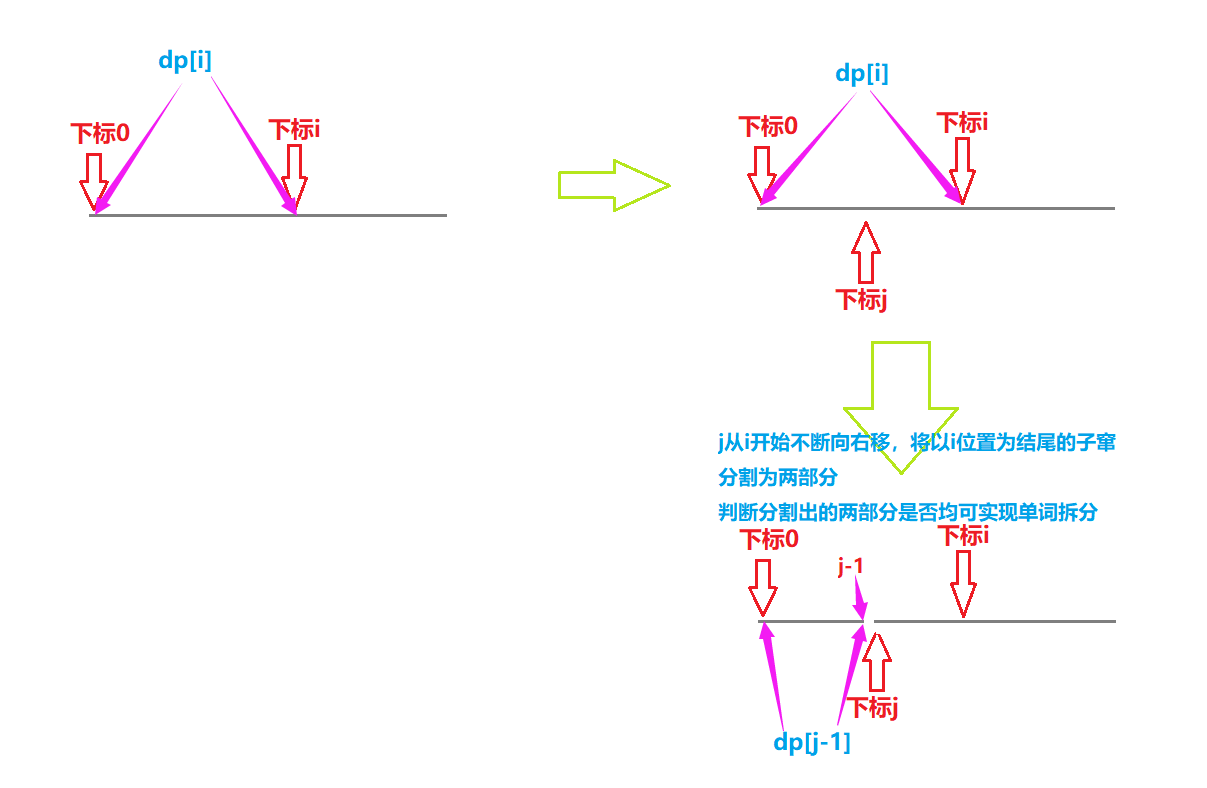
 我们可以定义dp[i]表示以i位置为结尾的子字符串是否能单词拆分。

状态转移方程推导：

 要判断从下标从0到i的子串是否能单词拆分。我们可以将0到i的字串分为两部分：0到j-1，j到i（0 <= j <= i）。而dp[j-1]表示以j-1位置为结尾的字串能否单词拆分的结果。此时我们还需判断下标从j到i的字串是否能单词拆分。此时即可判断此种分发是否能实现单词拆分！！
 但由于j的位置不确定。所以我们可以一次将j从开始，逐渐减小到起始下标0。在每次递减过程中，只有存在一种拆分发将拆分出的两个字串都能实现拆分单词，此时dp[i]=true,同时可停止遍历。否则为false;

细节处理：
 在填dp表过程中，dp[i]的值会用到dp[j-1]（0<=j<=i）,可能会发生越界访问。所以我们为dp表额外增加一个空间，同时为了保证后续填表的正确性，我们需要将dp[0]初始化为true。
 同时面对字符串问题时，通常需要存在子字符窜问题。此时，下标映射关系可能+1,可能减1。所以这里个原始字符串最开始任意增加一个字符（习惯上该字符为空字符），让原始字符串下标统一向后移动一位。
【代码编写】：

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_map<string, int> hash;for(auto& str : wordDict)//后续快速查找是否存在某单词hash[str]++;int n = s.size();vector<bool> dp(n + 1);dp[0] = true;//初始化，保证后续填表正确s = ' ' + s;//让s下标集体向后移动一位for(int i = 1; i <= n; i++)for(int j = i; j >= 1; j--){if(dp[j - 1] && hash.count(s.substr(j, i - j + 1))){dp[i] = true;break;}}return dp[n];}
};

四、环绕字符串中唯一的子字符串

【题目链接】：467. 环绕字符串中唯一的子字符串
【题目】：

【代码编写】：

 定义字符串 base 为一个 “abcdefghijklmnopqrstuvwxyz” 无限环绕的字符串，所以 base 看起来是这样的：

• “…zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd…”。
  给你一个字符串 s ，请你统计并返回 s 中有多少 不同非空子串 也在 base 中出现。

【示例】：

输入：s = “zab”
输出：6
解释：字符串 s 有六个子字符串 (“z”, “a”, “b”, “za”, “ab”, and “zab”) 在 base 中出现。

【分析】：
 我们可以定义dp[i]表示以i位置为结尾的字符串中非空字串在base中出现的个数。

状态转移方程推导：
 非空字串存在于base中有两种可能：

1. 相邻字符是连续的，即s[i-1] + 1 == s[i]。
2. 相邻字符分别是26个小写字母的结束和开始，即是bashs[i-1] == 'z' && s[i] == 'a'。
   所以状态转移方程为：

if((s[i] - s[i - 1] == 1) || (s[i - 1] == 'z' && s[i] == 'a'))dp[i] = dp[i - 1] + 1;

细节处理：
 由于当个字符一定存在于base中，所以dp[i]的值最小为1，所以我们可以将dp表中的初始值全部初始化为1。

 上述dp表中的结果存在重复值，不能直接累加。那如何去重？

• 我们知道以某一个字符为结尾的子串中，长子串一定包含了短子串的所有结果。所以我们可以借助一个26空间大小的数组，将s分割出的字串中，以结尾字符为依据，将最长字串结果放入对应的数组空间中。从而实现去重效果。即：hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);
   既然以及去重了，最后只需将数组中的结果累加即可！！

 
【代码编写】：

class Solution {
public:int findSubstringInWraproundString(string s) {int n = s.size();vector<int> dp(n, 1);for(int i = 1; i < n; i++)if((s[i] - s[i - 1] == 1) || (s[i - 1] == 'z' && s[i] == 'a'))dp[i] = dp[i - 1] + 1;int hash[26] = {0};for(int i = 0; i < n; i++)//去重hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);int ret = 0;for(auto x : hash)ret += x;return ret;}
};

这篇关于算法沉淀——动态规划篇（子数组系列问题（下））的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---