SkipList 跳表

2024-04-01 22:44
文章标签 跳表 skiplist

本文主要是介绍SkipList 跳表，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 查询
  • 增加
  • 删除
  • 写法优化 GO版本
  • 题外话

最近在读 LevelDB 的源码，正好看到里面使用了跳表这种数据结构于是学习一下

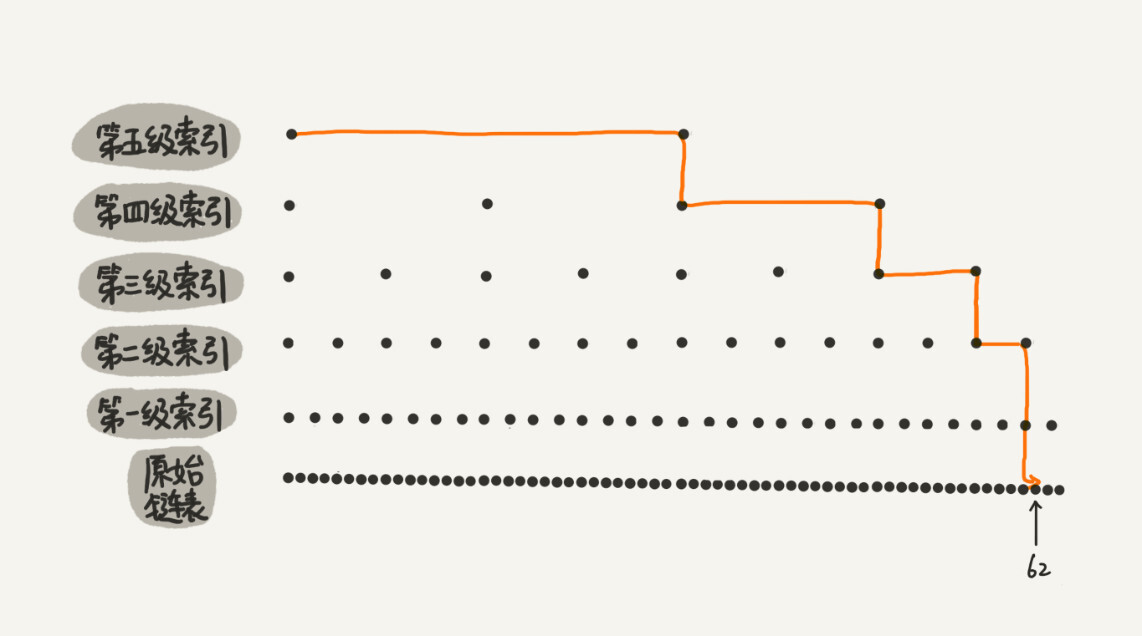
跳表实际上是由多个链表组成的，时间复杂度是O(logn)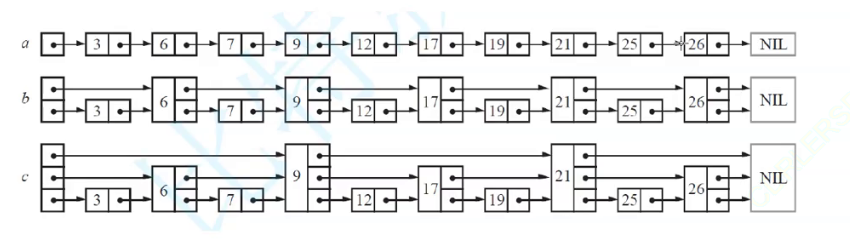
image.png
一种思路：

  • 每相邻两个节点升高一层，增加一个指针，让指针指向下一个节点
  • 以此类推，我们可以在第二层新产生的链表上，继续为每相邻的两个节点升高一层
  • 如果严格按照上面的设计来执行，那么调表的查询的时间复杂度时logN，但是插入和删除结构不太好，因为需要大范围的调整结构，来维护规则二 。

上面所述 的规则如果严格执行，查询的效率会很高，但是插入和删除会十分麻烦，所以跳表采用概率 在尽量不增加时间复杂度的同时 ， 更加容易 插入和删除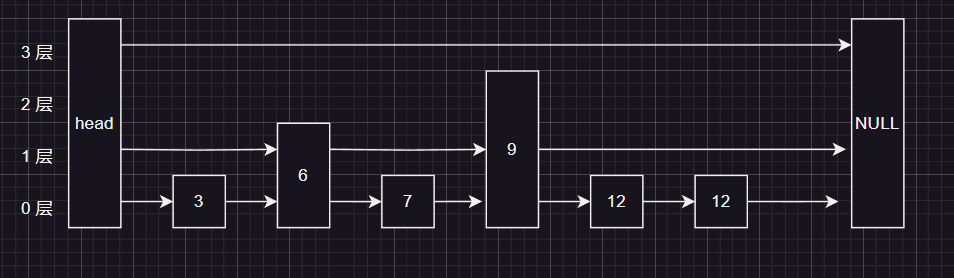
image.png

  • 整个跳表会有一个节点的最大高度maxlevel，跳表所有节点的高度 都不会超过这个maxlevel
  • 跳表会维护一个头节点，头结点后面都是插入的数据
  • 跳表以null ，作为链表的终点

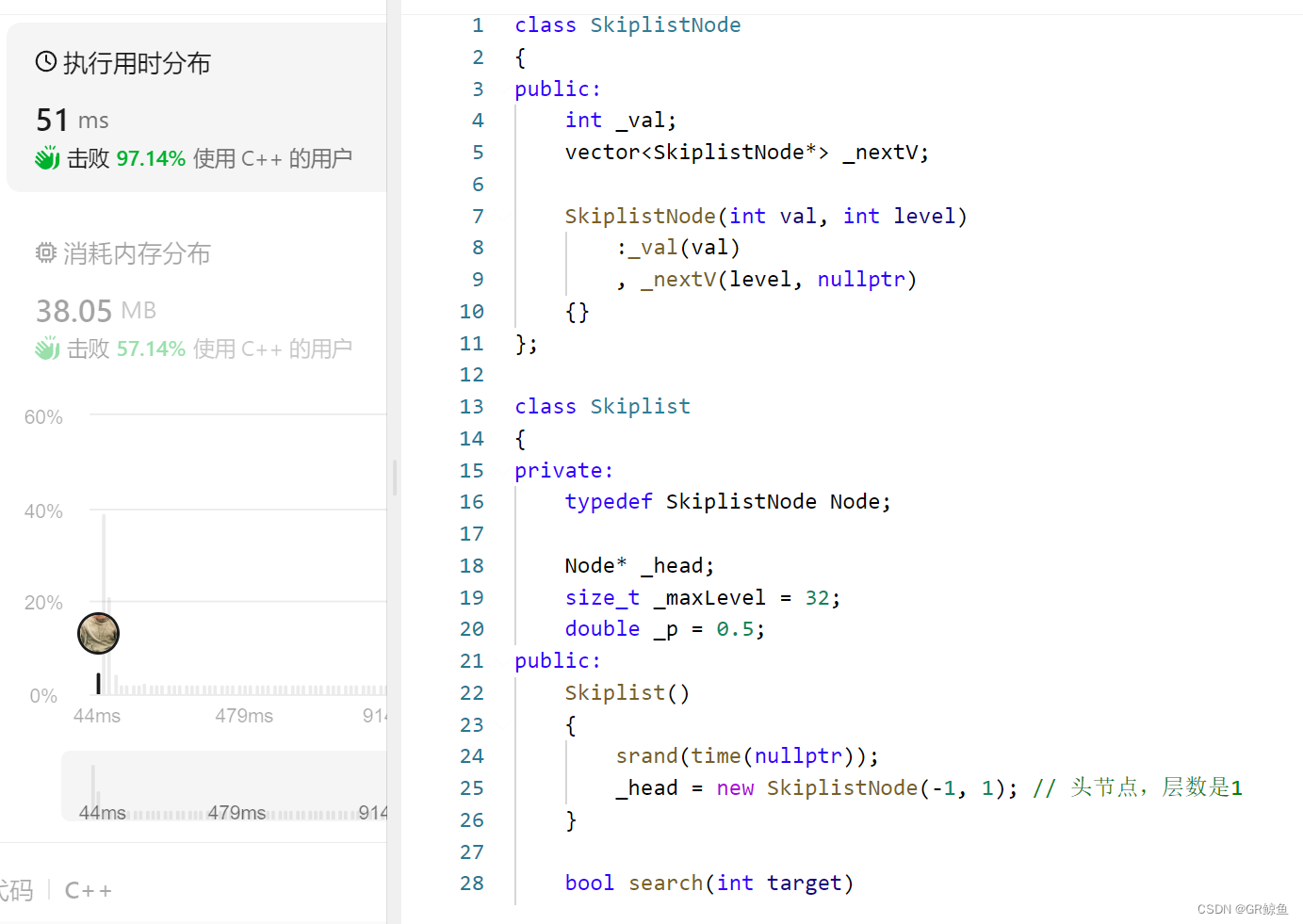
下边是一个跳表的简单结构，节点的定义如下:

class Node {
public:// 这个maxlevel  是 跳表的最大层数，我们这边先把空间开辟好，防止扩容造成不必要的拷贝Node(int v = -1, int maxlevel = 0) :val(v) {next.reserve(maxlevel);}int val;  // 节点存储的值vector<Node*> next;  // 当前节点的层数
};

那么一个节点的有几层该如何确定呢？ 这就是跳表的精髓，首先我们有一个概率p，这个p代表有多大几率节点层数+1，请看下面的一段伪代码，v代表节点的层数，maxlevel 是跳表的最大层数 ，rand 是[0,1]的随机值

int v=1;
while(v< maxlevel &&  rand()< p){v++;
}

按照上面的代码 我们可以随机的取到每一个新节点的层数 ，如果数据量足够大的时候 ，每一次的概率理论上应该为：

层数概率
1层1-p
2层p*(1-p)
3层p^2*(1-p)

后面以此类推 就不在列举了，所以如果数据量为N（数据量足够大），那么每一层的 数量 就是 概率*N，假设在这里的p==0.5，我们就可以推出 一层大概有 二分之一的数据 、二层大概有四分之一的数据… 至于为什么这样做的时间复杂度 为log(N)就不在我们的讨论范围之内，有兴趣的可以自己查一查论文。

下面就是跳表的实现部分，这里我是按照 leetcode 上的一道题目来完成的，这道题就是让我们设计一个跳表，最后还有测试用例 ，这就很舒服，可以验证我们的跳表的正确性

查询

如何在跳表中查询一个元素？ 这个十分简单，总结下来就是下面几个规则：

  1. 如果查询的值 比 当前层下一个节点大 向右走
  2. 如果查询的值 比 当前层下一个节点要小 || 当前层下一个节点为NULL 向下走
  3. 查询都是 当前节点的最大层数向下查询
  4. 当层数 小于0 的时候就应该跳出循环了

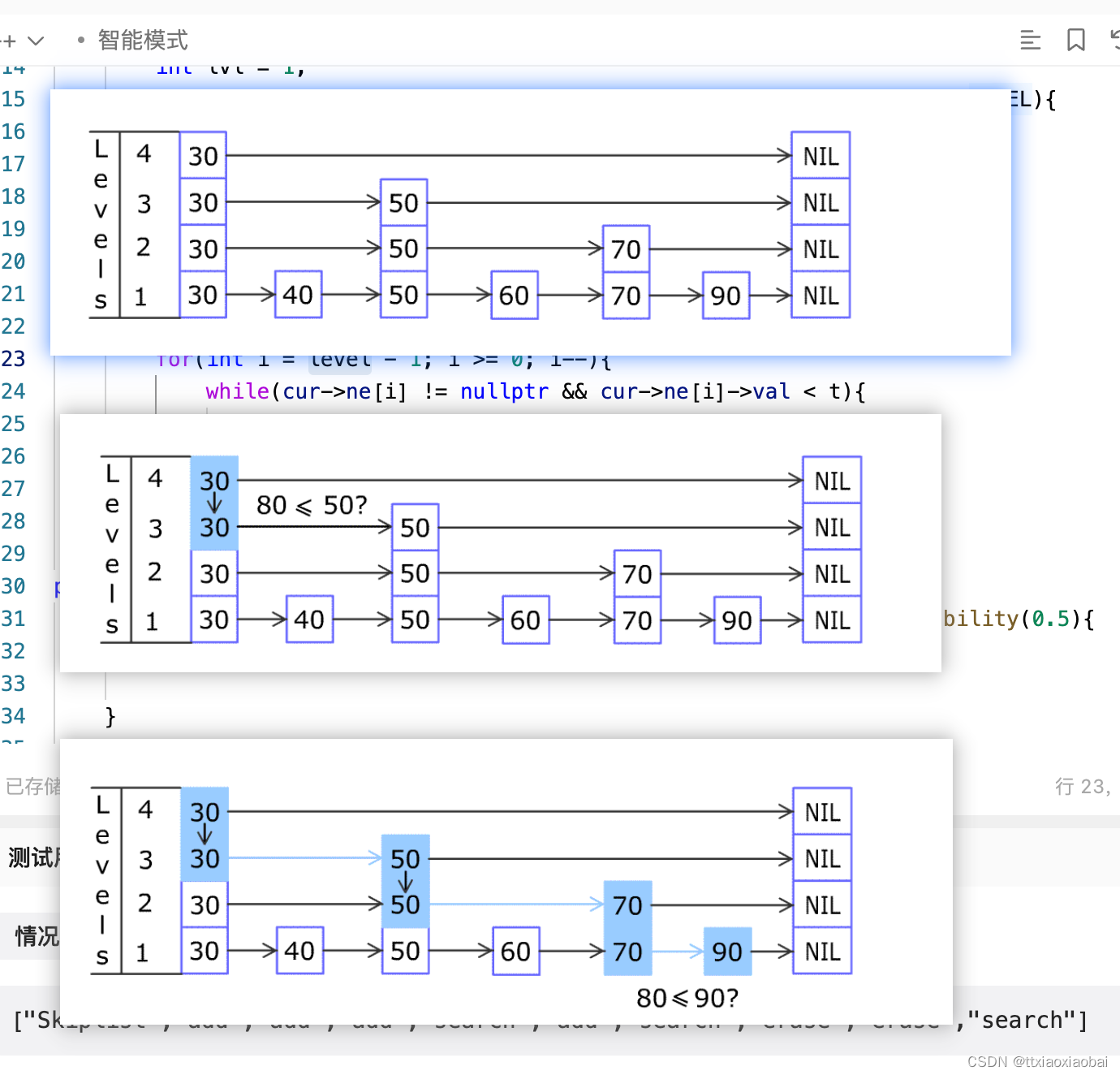
以下面这个跳表为例：我们要查询元素7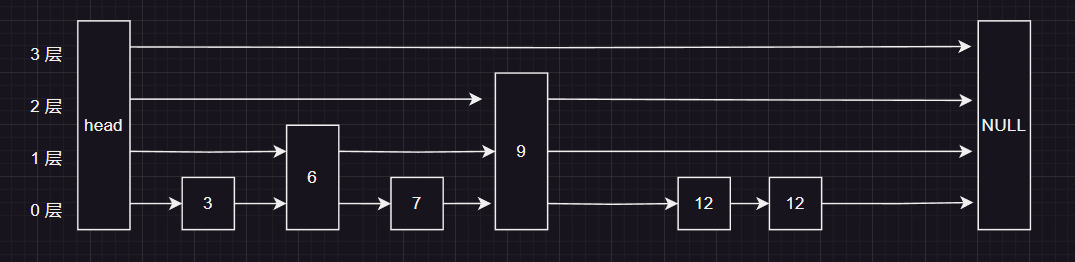
image.png

下面查询的所有画图 9 号节点 应该有一个箭头 指向null ，我是画完才发现的，☝这个是正确的，但是并不影响查询的逻辑我就不改了哈😋

首先我们从头结点的最大层出发，首先我们判断出 ，下一个几点为null，所以要查询的节点一定在第三层的下面的层数的链表中

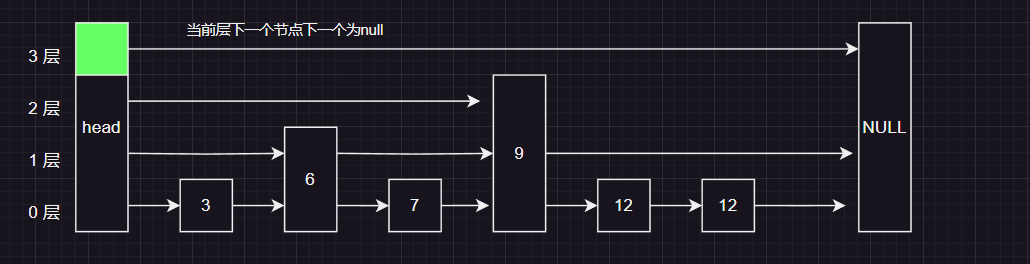
image.png

来到头结点的第二层 ，我们发现 第二层的下一个几点9 比我们要查询的7 要大 ，所以按照规则继续向下走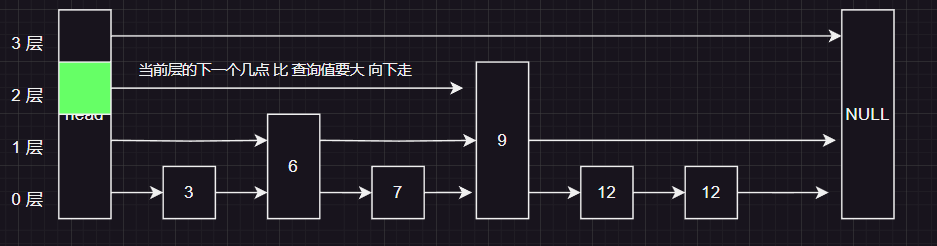
image.png

这时我们来到了头结点的第一层，我们发现下一个节点 比 7 小，按照规则我们应该向右边走

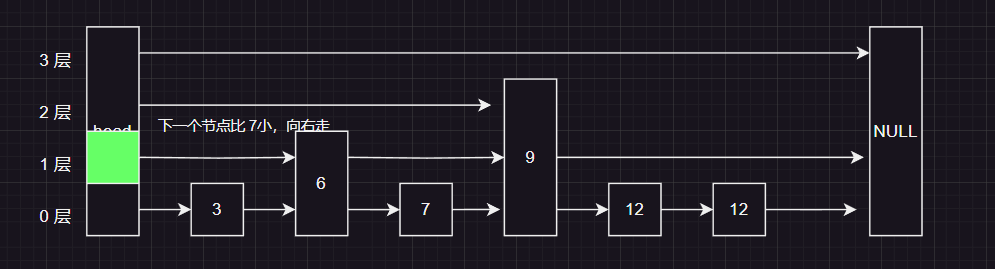
image.png

7 比当前节点在第一层的 下一个节点要小，所以向下走！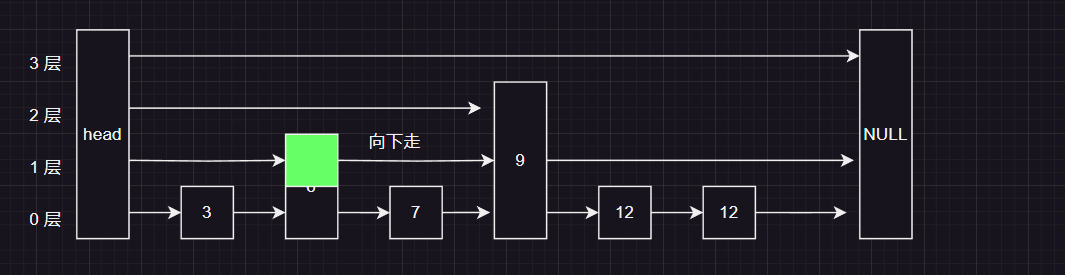
image.png

最后我们在来到了当前节点的的第0层，发现下一个节点就是我们要找的7，所以直接返回找到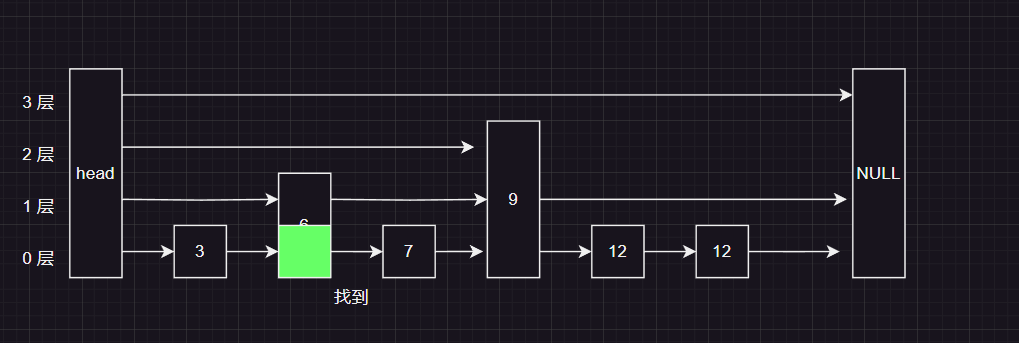
image.png

所以查询的代码如下：
如果对判断条件 curLevel >= 0不太理解的读者，可以带入一个跳表中不存在的值，再走一下流程就能理解了！

class Node {
public:Node(int v = -1, int maxlevel = 0) :val(v) {next.reserve(maxlevel);}int val;vector<Node*> next;
};class Skiplist {
public:Skiplist() :head(-1, maxlevel) {head.next.resize(maxlevel);}// next 比target 大向下走// next 比target小 向右走bool search(int target) {Node* cur = &head;int curLevel = head.next.size()-1;// 如果查询的层出小于0 代表找不到while (curLevel >= 0) {if (cur->next[curLevel] == nullptr || cur->next[curLevel]->val > target) {curLevel--;}else if (cur->next[curLevel]->val < target) {cur = cur->next[curLevel];}else // cur.next[curLevel]->val == targetreturn true;}// 如果走到这里 都没有return 那么代表 跳表中不存在target 直接返回falsereturn false;}private:double p=0.5;//std::default_random_engine e;int maxlevel = 4;Node head;
};

增加

增加和删除是一个思路，所以这里我们重点介绍一下插入的思路：
因为按照leetcode 题目的意思我们是可以插入重复的元素，所以我们要在当前跳表中插入元素12，先不介绍如何插入一个节点，我们观察一下下面的链表，我们认为 12 这个节点有两个插入的位置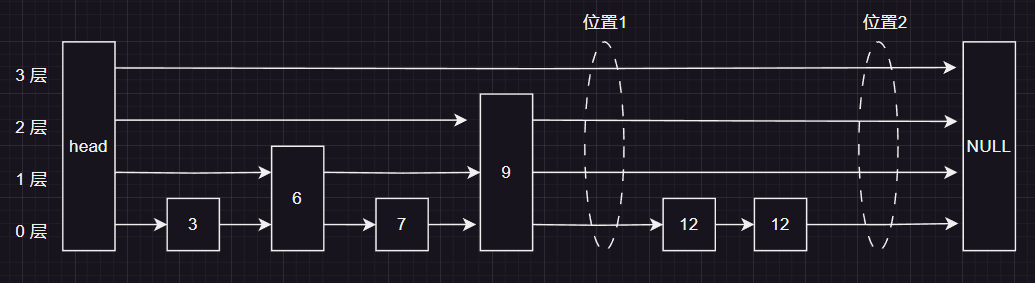
image.png
这里我写的这个版本是在位置2 插入的，最后给的那一版GO语言的版本 是在位置1 插入的！ 大伙可以对比着看一下👀
我们发现 如果我们要插入一个节点，我们得找到两个东西：

  1. 首先就是上图椭圆的位置，只有找到这个位置才能知道在哪里插入
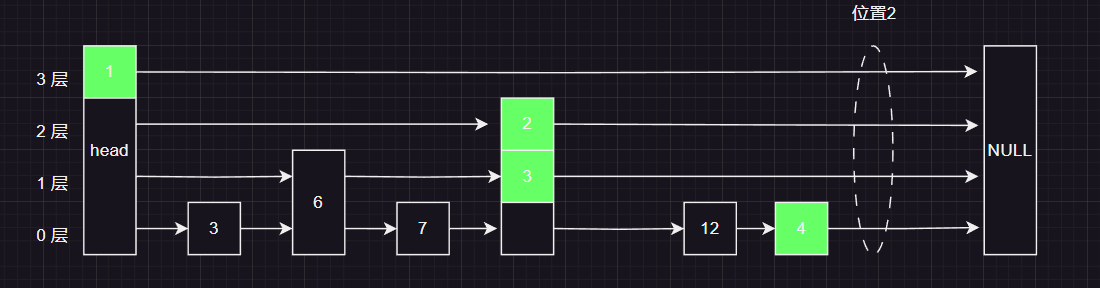
  2. 其次就是找到插入位置 ，每一层对应的上一个节点 见下图的绿色的节点👇image.png

这些节点我们可以在上面的查找过程中用一个数组（数组的长度等于）记录下来，记录这个节点的规则也十分简单只有一条：
向下走之前 把当前节点记录下来，记录到对应层的数组位置上！

我们首先创建一个 大小和跳表 maxlevel 层数相同的 pre 数组用来记录位置2 的每一层的前一个节点

首先我们还是从 头结点的最高层 开始，发现当前层的下一个节点是空，应该向下走，并将该节点入到数组的入到pre 数组的第三层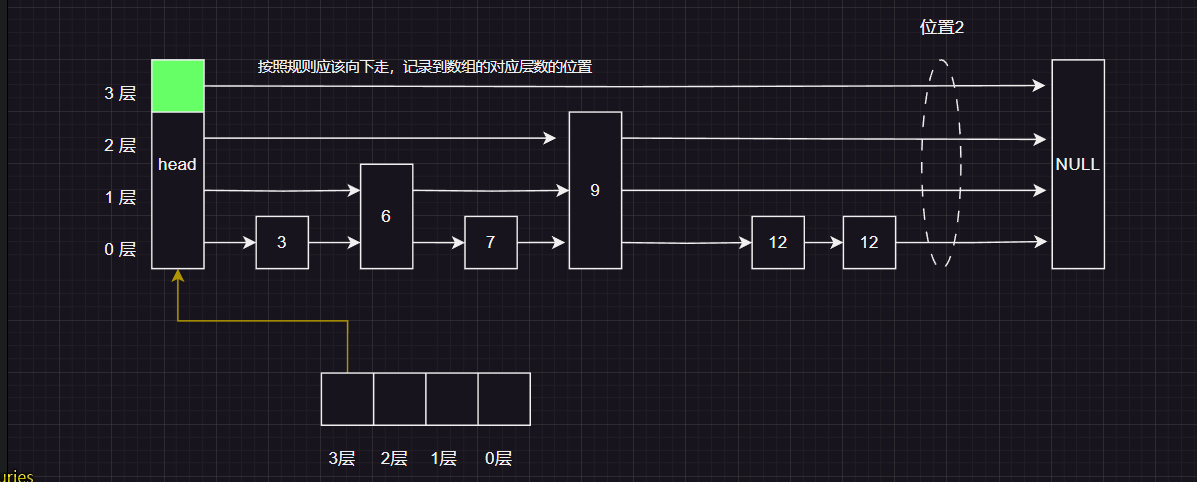
image.png

这时候我们发现 当前层的下一个节点的值 比 插入的值 要小应该向右走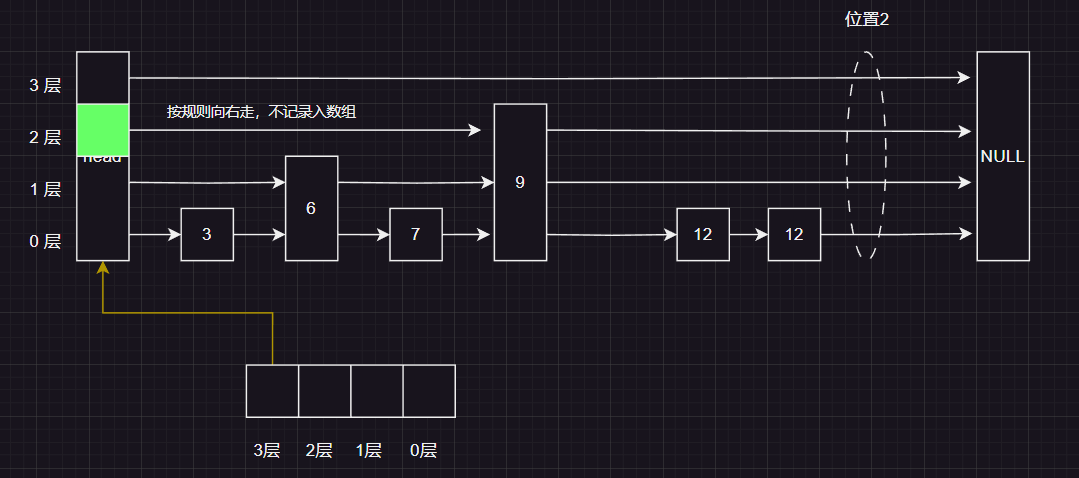
image.png

这时候 按照规则判断应该向下走 ， 并且 记录到pre 数组的对应位置上，

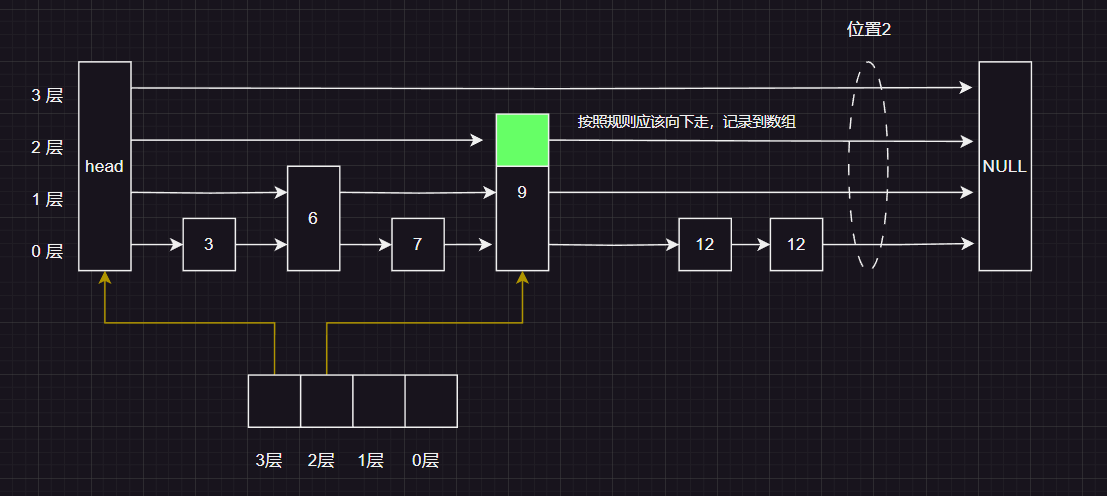
image.png

按照规则应该向下走 ，并且记录到pre 数组对应的位置上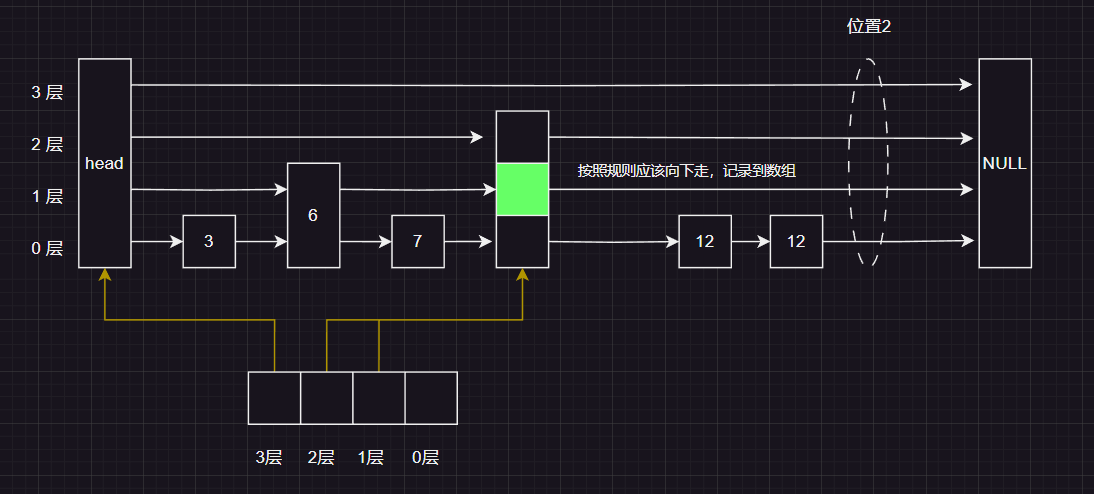
image.png

这时候我们发现 下一个节点 等于我们要插入的值 ，现在有两种选择：

  1. 如果相当向右走 ， 那么最终插入的位置是 位置2
  2. 如果向下走，那么最终插入的位置是 位置1

这里我们选择继续向右走，插入 位置2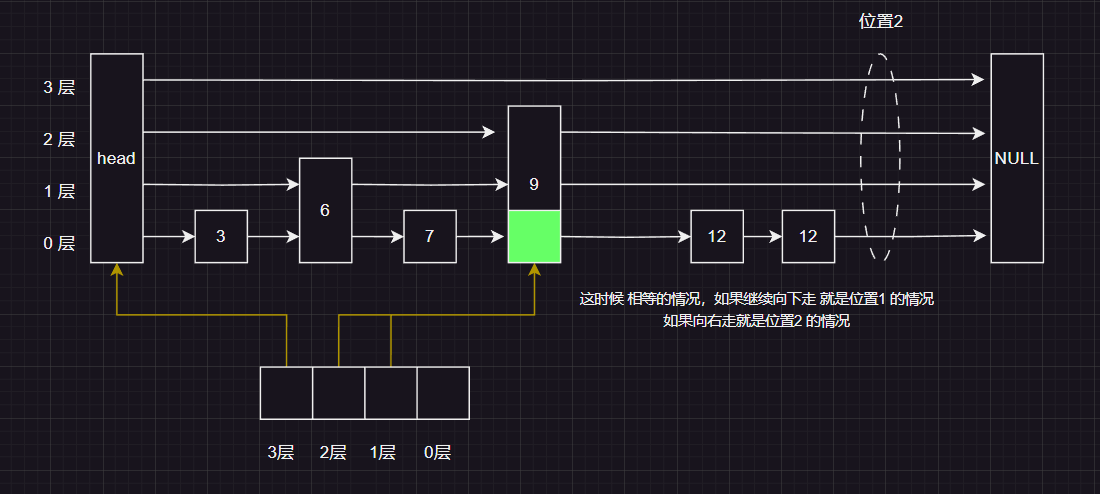
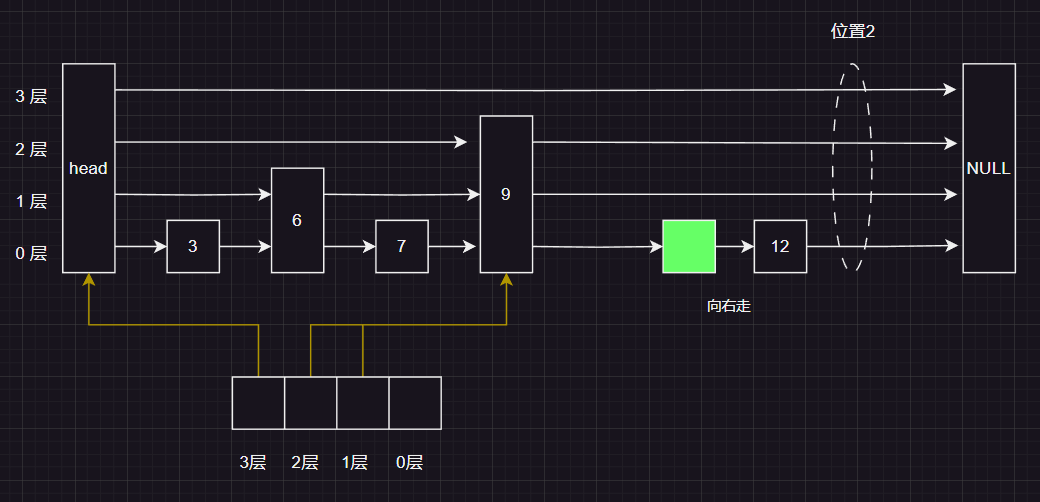
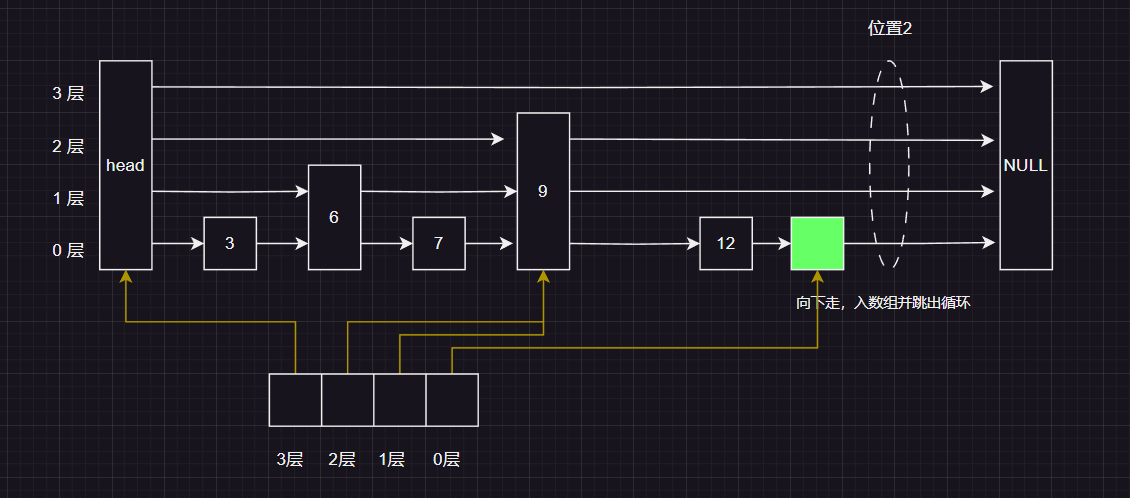
image.png

image.png
image.png

走到这里 ， level 减到-1 ，直接跳出循环，我们也找到了 插入的位置 和 该位置对应所有层的前置节点 。接下来就是 ：

  1. 确定插入节点的层数
  2. 插入节点

如何确定 插入节点的层数我们上面已经介绍过了，这里直接贴一个实现：
注意 RAND_MAX 是一个宏 ，rand函数取的值不会超过这个宏定义的值

  int RandomLevel() {int v=1;while(v< maxlevel &&  rand()< RAND_MAX * p){v++;}return v;}

接下来就是简单的链表插入，但是注意需要把新节点的所有层数都插入到对应层链表里面

下面示例的是 如果随机的值 是两层 ，那么最终插入的结果就是：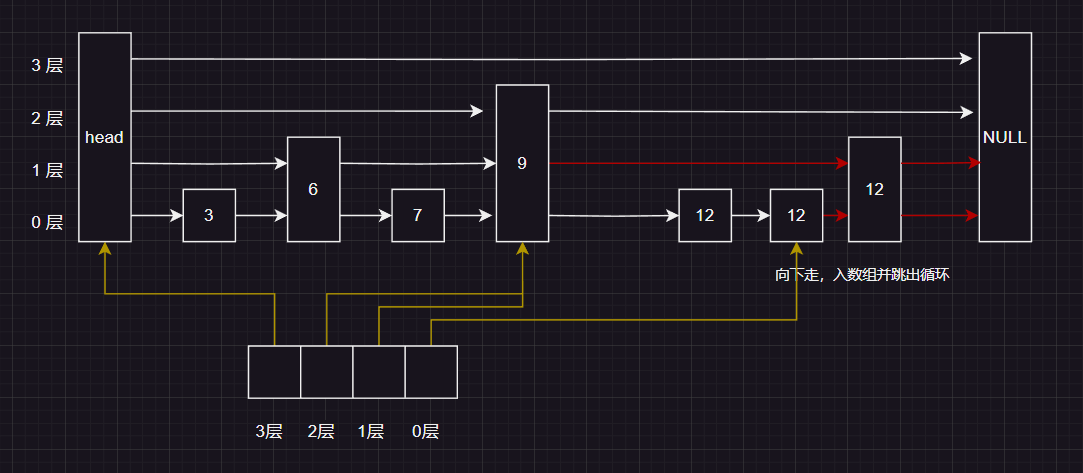
image.png
到这里一个简单的跳表插入就已经完成了代码如下👇

class Node {
public:Node(int v = -1, int maxlevel = 0) :val(v) {next.reserve(maxlevel);}int val;vector<Node*> next;
};class Skiplist {
public:Skiplist() :head(-1, maxlevel) {head.next.resize(maxlevel);//srand(time(0));}int RandomLevel() {int v=1;while(v< maxlevel &&  rand()< RAND_MAX * p){v++;}//cout<<v+1<<endl;return v;}void add(int num) {vector<Node*> pre(maxlevel);Node* cur = &head;int curLevel = head.next.size()-1;while (curLevel >= 0) {if (cur->next[curLevel] == nullptr || cur->next[curLevel]->val > num) {pre[curLevel] = cur;curLevel--;}else if (cur->next[curLevel]->val < num) {cur = cur->next[curLevel];}else{cur = cur->next[curLevel];pre[curLevel] = cur;curLevel--;}}int rlevel = RandomLevel();Node* newnode = new Node(num, maxlevel);newnode->next.resize(rlevel);for (int i = 0; i < rlevel; i++) {newnode->next[i] = pre[i]->next[i];pre[i]->next[i] = newnode;}}
private:double p=0.5;//std::default_random_engine e;int maxlevel = 4;Node head;
};

删除

删除的逻辑 和 插入是一模一样的，这里就不详细介绍了 说一下思路：

  1. 找到删除的节点的位置，如果没有找到 直接返回
  2. 在查找删除节点的过程中记录 删除位置 对应每一层的前一个节点，得到一个pre 数组
  3. 最后就是更具删除节点的层数 ，对每一层的pre 数组做一个简单的链表删除！

实际上只有最后一步 和 插入不一样 ，插入的最后一步是 一个链表的插入，删除的最后一步是一个链表的删除😂

写法优化 GO版本

对于上面的代码过于冗余，查询、删除、增加 都有部分逻辑是公共的，可以提取出来放在一个公用的函数用来调用，但是非常适合初学者想明白逻辑 ，所以我前面讲解的时候使用的就是冗余的代码，下面给出一个Go语言版本的跳表，这个版本的把所有的公共逻辑都放到了Find函数中。

type Node struct {Val  intNext []*Node
}func CreateNode(val, level int) *Node {cur := new(Node)cur.Val = valcur.Next = make([]*Node, 0, level)return cur
}type Skiplist struct {maxlevel intp        float32Node
}func Constructor() Skiplist {var sk Skiplistsk.maxlevel = 8sk.p = 0.5sk.Next = make([]*Node, 8) // 头结点的高度直接设置为8sk.Val = -1return sk
}// 返回值 bool 有没有target 这个节点
// 返回值 []*Node 代表每一层的前一个节点的数组
func (this *Skiplist) Find(target int) (bool, []*Node) {pre := make([]*Node, this.maxlevel)flag := falsecur := &(this.Node)curlevel := this.maxlevel - 1for curlevel >= 0 {if cur.Next[curlevel] == nil || cur.Next[curlevel].Val > target {// 向下走pre[curlevel] = curcurlevel--} else if cur.Next[curlevel].Val < target {// 向右走cur = cur.Next[curlevel]} else {flag = truepre[curlevel] = curcurlevel--}}if flag {return true, pre}return false, pre}func (this *Skiplist) RabdomLevel() int {rand.Intn(10000)v := 1for v < this.maxlevel && rand.Intn(10000) < int(float32(10000)*this.p) {v++}return v
}func (this *Skiplist) Search(target int) bool {ret, _ := this.Find(target)return ret
}func (this *Skiplist) Add(num int) {_, pre := this.Find(num)l := this.RabdomLevel() // 新节点的 高度newnode := CreateNode(num, this.maxlevel)newnode.Val = numfor i := 0; i < l; i++ {tmp := pre[i].Next[i]pre[i].Next[i] = newnodenewnode.Next = append(newnode.Next, tmp)}
}func (this *Skiplist) Erase(num int) bool {ret, pre := this.Find(num)if ret == false {return false}cur := pre[0].Next[0]for i := 0; i < len(cur.Next); i++ {pre[i].Next[i] = pre[i].Next[i].Next[i]}return true
}

题外话

上了研究生之后，我们组导师有点压榨，很难抽出大把的时间来学习，现在的学习时间都十分零碎，可能上午半个小时，下午活干完了有半个小时的空余时间。以前我都是一整个下午 或 一整个上午用来学习。这弄得我十分难受，在这里吐槽一下，这也倒逼我开始改变策略，如果想要进步 那就要抓紧这些零碎的时间利用起来。以前我十分瞧不起这种零碎的时间 ，因为进度很小 没有啥成就感，但是坚持了一段时间 我发现实际学习进度也是在缓步推进的，于是我得出一个结论： 重点不是每天学习进度的多少 ，重点是每天都在坚持的去做、去学习 每天都持之以恒的做不管每天能推进多少）实际上是最重要的（因为现在确实很难平衡工作和学习，时间是真的不够用啊😭），实际上一段时间下来还是能积累下来很多东西的。
希望对你有帮助。

这篇关于SkipList 跳表的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/868328。

相关文章

[C++][数据结构][跳表]详细讲解

[C++][数据结构][跳表]详细讲解

目录 0.什么是跳表？1.SkipList的优化思路2.SkipList的效率如何保证？3.SkipList实现4.SkipList VS 平衡搜索树 && Hash 0.什么是跳表？ SkipList本质上也是一种查找结构，用于解决算法中的查找问题，跟平衡搜索树和哈希表的价值是一样的，可以作为key或者key/value的查找模型SkipList，是在有序链表的基础上发展起
阅读更多...
力扣1206--跳表

力扣1206--跳表

1206. 设计跳表 - 力扣（LeetCode） 挑战一下hard,果然难搞 参考 跳表的原理与实现 [图解]_跳表实现-CSDN博客 代码如下： struct Node{Node(Node* _right, Node* _down, int _val) :right(_right), down(_down), val(_val){}Node* right;Node* down;int
阅读更多...
【高阶数据结构(八)】跳表详解

【高阶数据结构(八)】跳表详解

💓博主CSDN主页:杭电码农-NEO💓   ⏩专栏分类:高阶数据结构专栏⏪   🚚代码仓库:NEO的学习日记🚚   🌹关注我🫵带你学习更多数据结构   🔝🔝 高阶数据结构 1. 前言2. 跳表的概念3. 跳表的特性分析4. 跳表的效率分析5. 跳表模拟实现7. 跳表和传统查找结构的对比8. 总结 1. 前言 跳表也是一种查找结构,和红黑树,哈
阅读更多...
数据结构与算法之美-跳表-极客时间学习笔记

数据结构与算法之美-跳表-极客时间学习笔记

二分查找是针对数组结构的，那么链表结构有没有类似的方法可以实现快速查找？ 按照以空间换时间的思路，我们把单链表想象成一本书，每个节点都是1页，那么快速搜索的方法就是建立目录索引（并非完全相同的概念，这里的索引也需要遍历，不能跳跃）。从一页页翻页变成在按照索引一个个查找，然后再下一层进入到节点层查找。 为了加快搜索速度，可以建立不止一级索引，上一层以下一层为基础，每次跳过1个元素（这里并
阅读更多...
leecode 1206｜跳表的设计

leecode 1206｜跳表的设计

跳表 跳表，一种链表数据结构，其增删改茶的效率能和平衡树相媲美 leecode1206 可以看上面的那个动画，动画效果很贴切。 我简单讲讲它的机制吧，每个节点不单单是一个，测试好几层，然后同一层的节点和统一节点的next 采用单链表产生联系 最核心的东西在于find 这也是为什么单链表的增删改查，花费开销最多的地方。 那它是怎么查的？ 我们已经知道了跳表的结构了，最底层肯定是
阅读更多...
其它高阶数据结构⑦_Skiplist跳表_概念+实现+对比

其它高阶数据结构⑦_Skiplist跳表_概念+实现+对比

目录 1. Skiplist跳表的概念 2. Skiplist跳表的效率 3. Skiplist跳表的实现 3.1 力扣1206. 设计跳表 3.2 Skiplist的初始化和查找 3.3 Skiplist的增加和删除 3.4 Skiplist的源码和OJ测试 4. 跳表和平衡搜索树/哈希表的对比 本篇完。 1. Skiplist跳表的概念         skipl
阅读更多...
redis并发之跳表

redis并发之跳表

简介 跳表（Skip List）是一种用于实现有序集合（Sorted Set）的数据结构，在 Redis 中被广泛应用。跳表的设计旨在提供高效的有序集合操作，可以将跳表理解为基于二分查找的索引结构。跳表通过构建多层索引，每一层索引都是前一层索引的子集，形成一种分层递进的结构。每个索引节点中存储了对应层级的元素，通过这些索引节点可以快速定位到目标元素所在的区间，然后在目标区间内进行二分查找。 跳
阅读更多...
redis核心数据结构——跳表项目设计与实现（跳表结构插入数据、删除数据、展示数据）

redis核心数据结构——跳表项目设计与实现（跳表结构插入数据、删除数据、展示数据）

数据的插入 首先来看需求 你的任务是实现 SkipList 类中搜索节点和插入节点的成员函数。  插入节点成员函数签名：int insert_element(const K key, const V value)  向跳表中插入一对数据，如果跳表中已存在该键值对，则不做任何操作，返回 1，如果不存在该键值对，则将该键值对插入到跳表中，返回 0。  参数说明： K key：键； V valu
阅读更多...
redis核心数据结构——跳表项目设计与实现（跳表结构介绍，节点类设计，随机层级函数）

redis核心数据结构——跳表项目设计与实现（跳表结构介绍，节点类设计，随机层级函数）

跳表结构介绍。跳表是redis等知名软件的核心数据结构，其实现的前提是有序链表，思想的本质是在原有一串存储数据的链表中，间隔地抽出一半元素作为上一级链表，并将抽提出的元素和原先的位置相关联，这样重复下去直到最上层只有一个节点。构建时比较复杂，但在查找元素时可以达到log(n)的时间复杂度。这也就是跳表这一名称的由来了。 此外等会要写ACM模式，cin cout大家都知道是iostream里面
阅读更多...
为什么MySQL使用B+树而不是跳表

为什么MySQL使用B+树而不是跳表

1. 磁盘IO效率问题 MySQL是基于磁盘存储系统，而B+树的设计就很符合磁盘存储系统，它可以最大化地减少磁盘IO操作。而磁盘IO的读写速度远小于内存的读写速度，所以减少磁盘IO操作对于MySQL性能的提升至关重要，与之相对，Redis是基于内存的，所以可以使用跳表而不是B+树，它不需要磁盘的IO操作。以下是B+树减少磁盘IO的几个关键点： 高扇出度：B+树的每个节点可以包含大量的键值对。这
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2