算法沉淀 —— 深度搜索（dfs）

本文主要是介绍算法沉淀 —— 深度搜索（dfs），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、计算布尔二叉树的值

【题目链接】：2331. 计算布尔二叉树的值
【题目】：

【分析】：
 在确定一颗二叉树的布尔值前，我们需要先得到左子树、右子树的结果(0/1)。如果左子树、右子树不是叶子节点，显然这是一个递归子问题（将求左子树、右子树的布尔值）；
 最后就是根据root的值来判断对左/右子树结果的操作（如果是2，按位或；否则为按位与）

【代码实现】：

class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left == nullptr && root->right == nullptr)return root->val;//完成二叉树保证如果非叶子节点，则左右子树都不为空bool ansL = evaluateTree(root->left);//递归处理左子树bool ansR = evaluateTree(root->right);//递归处理右子树return root->val == 2 ? ansL | ansR : ansL & ansR;}
};

二、求根节点到叶节点数字之和

【题目链接】：129. 求根节点到叶节点数字之和

【题目】：

【分析】：
 根节点到叶节点数字之和，显然如果当前节点为叶子节点，此时直接返回结果；否则需要得到当前路径之前路径和（假设为prev），此时当前路径数字和为root->val + prev*10。此时在重复上述过程，如果时叶子节点，直接返回结果；否则转化为递归子问题求解（左子树、右子树只有非空，都有结果）
 由于根节点到叶节点的路径可能存在多条，每一条路径都存在一个结果。所以这里我们可以定义一个全局变量来记录最后的累计结果。（具体看代码）
【代码实现】：

class Solution {
public:int sum = 0;int sumNumbers(TreeNode* root) {int prev = 0;_sumNumbers(root, 0);//prev用于记录当前节点前的路径和return sum;}void _sumNumbers(TreeNode* root, int prev){prev = prev * 10 + root->val;//还是使用prev来保存当前路径数字和if(root->left)//左子树非空，必然存在结果，转化成递归子问题求解_sumNumbers(root->left, prev);if(root->right)//右子树非空，同上_sumNumbers(root->right, prev);if(root->left == nullptr && root->right == nullptr)//叶子节点, 累加当前路径和sum += prev;}
};

三、二叉树剪枝

【题目链接】：814. 二叉树剪枝
【题目】：


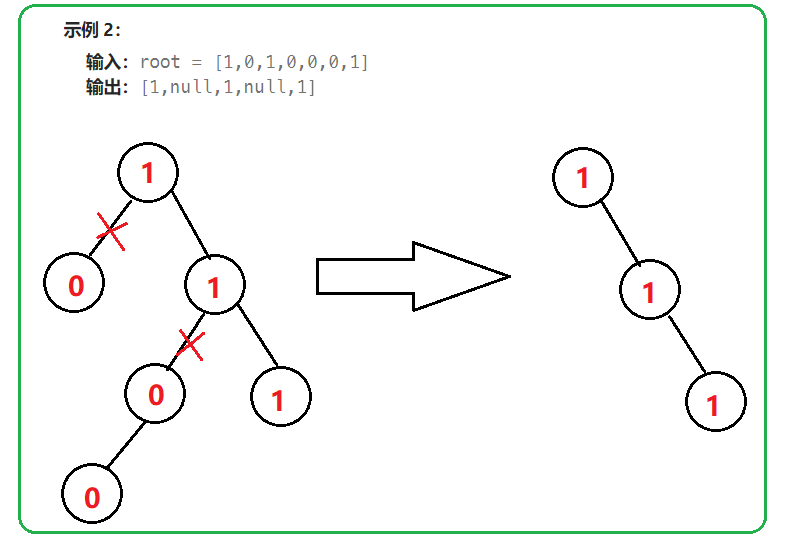
【分析】：
 本题中，我们可以采用二叉树后序遍历的思想。先对左子树、右子树分别进行剪枝操作。此时左/右子树中有两种结果：非空、非空(此时子树已经进行了剪枝)。所以此时当前节点必须满足左/右子树均为空，并且根节点为0时，才可继续剪枝。
【代码实现】：

class Solution {
public:TreeNode* pruneTree(TreeNode* root) {//二叉树后序遍历，进行剪枝//对左/右子树剪枝后，左/右子树只有两种结果: 为空、剪完枝非空。if(root == nullptr)return nullptr;root->left = pruneTree(root->left);//对左子树剪枝root->right = pruneTree(root->right);//右子树剪枝if(root->left == nullptr && root->right == nullptr && root->val == 0){delete root;//笔试建议省略此步，原因在于如果root不是new出来的，会报错root = nullptr;}return root;}
};

四、验证二叉搜索树

【题目链接】：98. 验证二叉搜索树
【题目】：

【分析】：
 我们可以利用二叉搜索树中序遍历是升序的性质来判断是否为二叉搜索树。但如何利用呢？
 其中一种思路是先用一个数组记录二叉树中序遍历结果，在判断是否为升序。但此时算法的空间复杂度为O(n)。
 另一种思路就是使用一个全局遍历(prev)来记录中序遍历的前一个数据，然后转化成当前节点和prev比较（当然还有prev值更新啦）。让后根据左子树、右子树、根节点的结果来判断是否符合AVL树（具体参考代码）
tips:

• prev的初始值需要设置为LLONG_MIN（比INT_MIN小即可）。
  【代码实现】：

class Solution {
public:long long prev = LLONG_MIN;//保存中序遍历的前一个节点值bool isValidBST(TreeNode* root) {if(root == nullptr)return true;bool Left = isValidBST(root->left);//记录左子树结果bool cur = false;//记录当前根节点和上一个数据是否符合AVL树性质if(root->val > prev){prev = root->val;cur = true;}bool Right = isValidBST(root->right);//记录左子树结果return Left && Right && cur;}
};

五、二叉搜索树中第K小的元素

【题目链接】：230. 二叉搜索树中第K小的元素
【题目】：

【分析】：
 本题意思非常明确，求第k小元素。我们可以通过中序遍历，每遍历一次元素，k–。直到k为1时，返回结果。
 这里博主推荐将返回值(定义为ret)、和k的值都设置为全局变量。然后和中序遍历一样，我们只需当k的值为1时，返回结果结果；并且每次遍历k–。
【代码实现】：

class Solution {
public:int count = 0, ret = 0;int kthSmallest(TreeNode* root, int k) {count = k;_kthSmallest(root);return ret;}void _kthSmallest(TreeNode* root){if(root == nullptr || count == 0)return;_kthSmallest(root->left);if(--count == 0)ret = root->val;_kthSmallest(root->right);}
};

这篇关于算法沉淀 —— 深度搜索（dfs）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---