本文主要是介绍正多边形拓扑与泛函,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
(原创:Daode3056)
也许,关于“拓扑”,“泛函”几本书上的内容与实例都是大同小异,总是那么点内容,数学要开拓一些新领域与新内容才能满足不断发展的社会与工业各种需要。本文就以人工智能生成对称图案为切入口,再抛砖引玉,可让读者既可对照那些理论深挖,也可用于各种工艺、建筑、日用品、场馆、镭射等应用。
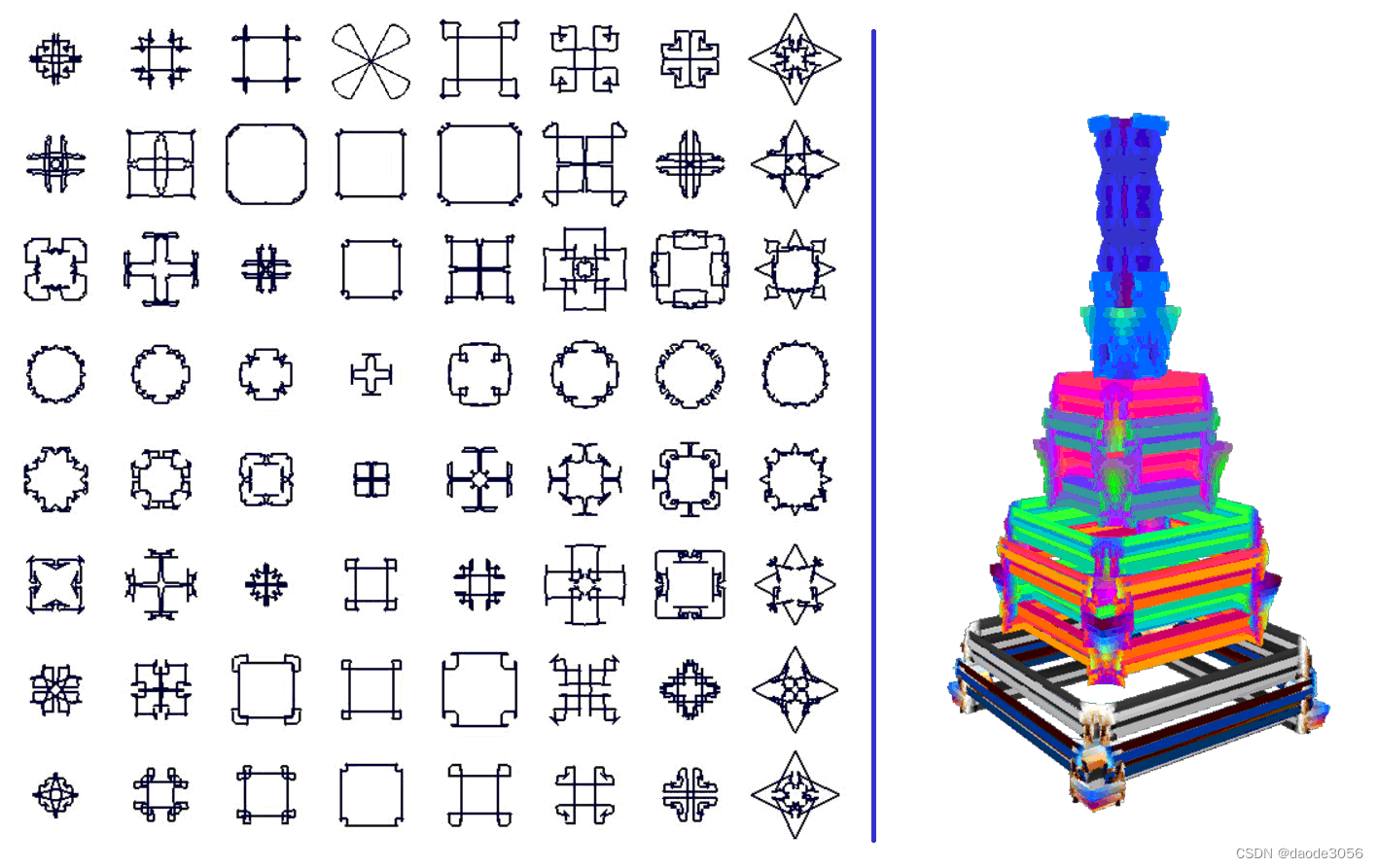
效果图一则:
一,我们可以通过复变函数生成正N边形的顶点,这N最好是4的倍数。公式如下:
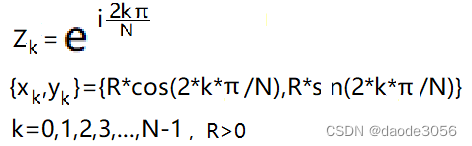
二,自己构造一些混沌算子,用于对上述各顶点移动,视作拓扑变换 ,测试各迭代器工作状态,以便混沌算子能正常地工作:如作者的七种算子如下:
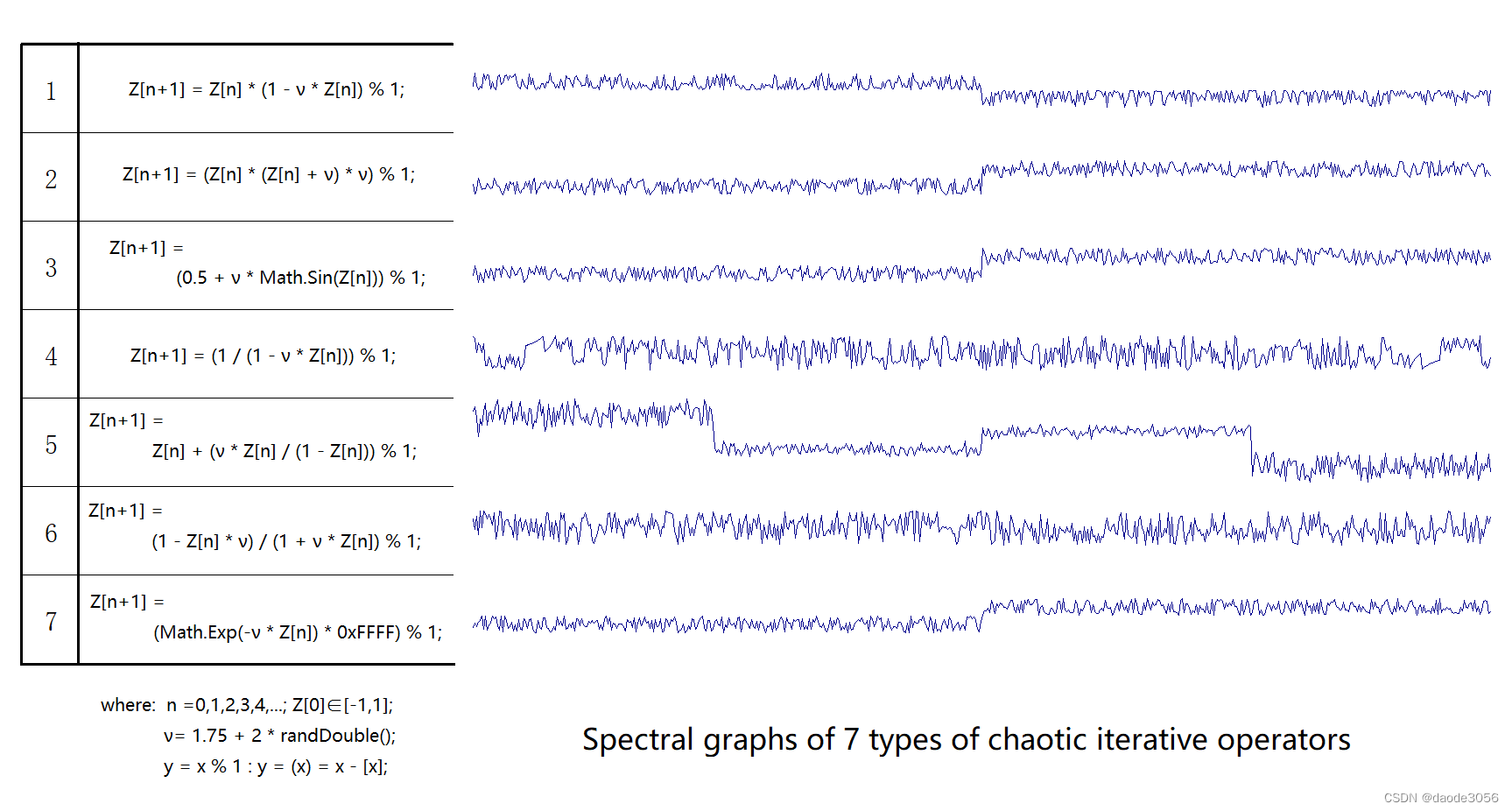
就表中第一种迭代器对数据的处理,细节表现是下图:
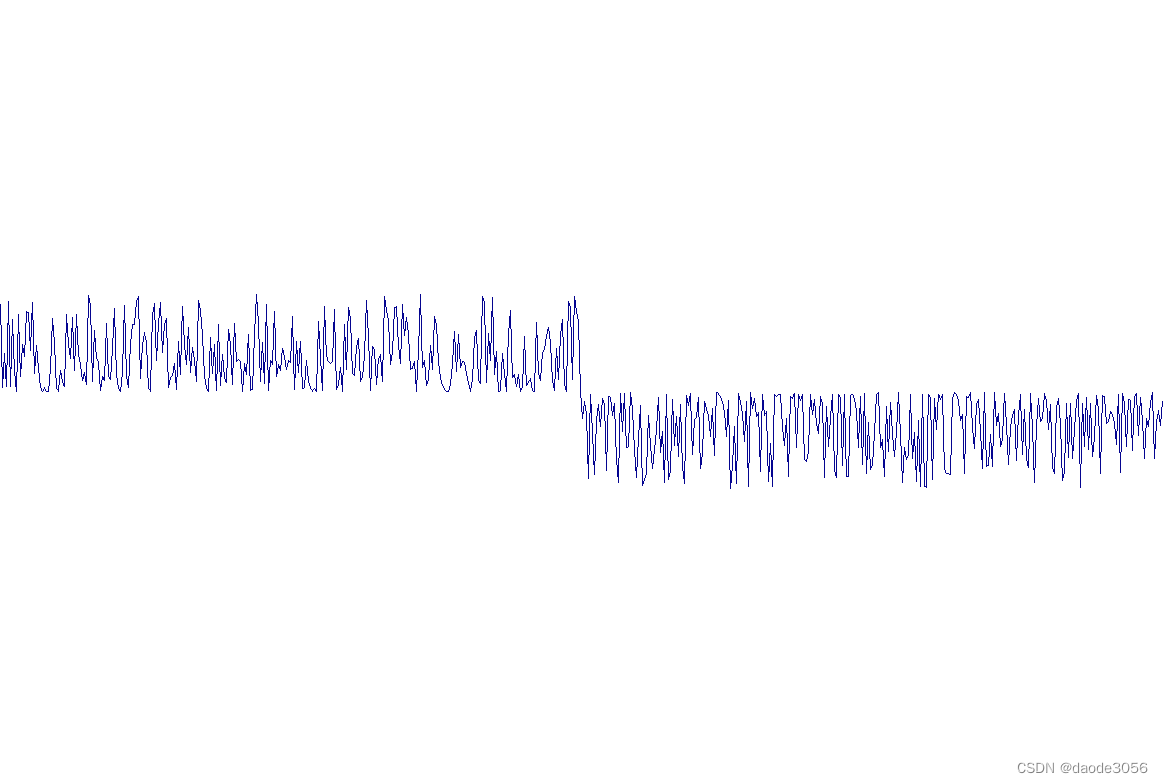
实测的局部数据图表如下:
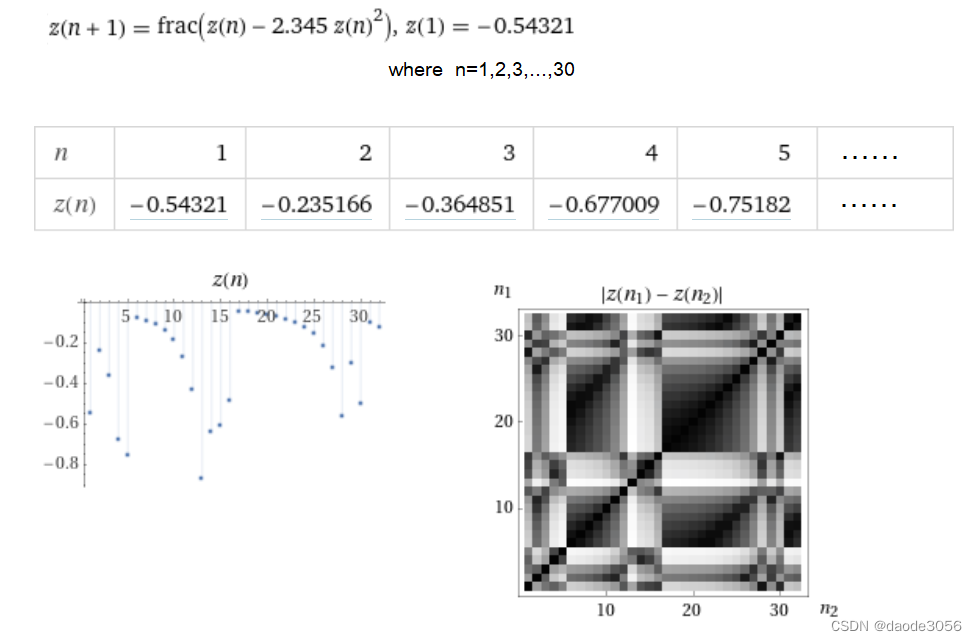
使用上述迭代算法变换N个点的坐标,然后使用贝塞尔平滑算法(线条是绿色图)进行插值,或者直接绘制一簇折线(蓝色的),形成下图(7行*10列=70个图):

模仿,再处理第二种迭代算法,得到下图:

这样,我们可以用不同的算法构造更多的造图函数,进行求和。这里的泛函可以使用以下表达式:

有了这样的泛函,我们用于在图像是叠加,能产生更多奇妙的图像。
其他算法的:

叠加效果的有:

二进制变换就更加灵活多样,文章开头的图像也是二进制变换所产生:

这样,在针对正多边形的拓扑上,我们就获得了丰富的对称图案,它是机器辅助人们进行图案、商标、工艺设计的好帮手。其中,要研究泛函的一些性质、定理,如维度、线性、封闭性等等,还是大有文章可做的。作者是机器人与视觉方面的程序猿,这是给各位的小甜饼。
原创作者:项道德,2024-03-31
这篇关于正多边形拓扑与泛函的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!