正多边形专题
Codeforces 1C. Ancient Berland Circus(计算几何:正多边形性质+高精度)
给出三个点的坐标,输出含这三个点的最小正多边形面积 感觉这个题太牛逼了。。。 做的我元气大伤,昨晚看的题,一直没有思路 就去找了道类似的计算几何题Uva12300来做,做得还是挺顺手的 后来意识到了正多边形的一个性质:正n边形中一条边对应的圆心角为2×PI/n 以这里为突破口,先找出n的值,进而再求解 但有一个问题就是给定的点不一定相邻 也就是说两个点与圆心所对应的夹角有可能是多条边
c++【入门】正多边形每个内角的度数
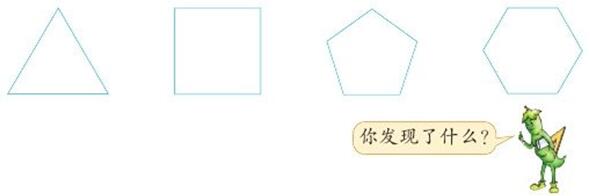
限制 时间限制 : 1 秒 内存限制 : 128 MB 题目 根据多边形内角和定理,正多边形内角和等于:(n - 2)×180°(n大于等于3且n为整数)(如下图所示是三角形、四边形、五边形、六边形的形状) 请根据正多边形的边数,计算该正多边形每个内角的度数。(结果保留1位小数) 输入 正多边形的边数n(n>=3 且 n <= 10) 输出 该正n边形每个内角的度数。
东方博宜1317 - 正多边形每个内角的度数?
问题描述 根据多边形内角和定理,正多边形内角和等于:( n-2 ) × 180∘( n 大于等于 3 且 n 为整数)。 请根据正多边形的边数,计算该正多边形每个内角的度数。(结果保留1位小数)。 输入 正多边形的边数 n ( n≥3 且 n≤10 )。 输出 该正 n 边形每个内角的度数。 样例 输入 3 输出 60.0 代码1 #include <iostream>u
软件测试|教你使用Python绘制正多边形
简介 绘制正多边形是Python图形编程的基本任务之一。在本文中,我将为你提供一个使用Python绘制正多边形的详细教程,并提供一个示例代码。我们将使用Python的Turtle库来进行绘制。 步骤1:导入Turtle库 我们需要先安装好Python环境,然后我们使用Turtle库来进行图形绘制。Turtle库是Python标准库的一部分,无需额外安装。 步骤2:创建一个Python脚
【Scratch画图100例】图47-scratch绘制双层旋转正多边形 少儿编程 scratch编程画图案例教程 考级比赛画图集训案例
目录 scratch绘制双层旋转正多边形 一、题目要求 1、准备工作 2、功能实现
绘制彩色正多边形-第11届蓝桥杯选拔赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第10讲。 绘制彩色正多边形,本题是2019年~2020年举办的第11届蓝桥杯青少组Python编程选拔赛真题(具体日期不详),题目要求根据所给图片识别出图形中的基本形状,以基本形状为单位绘制出最
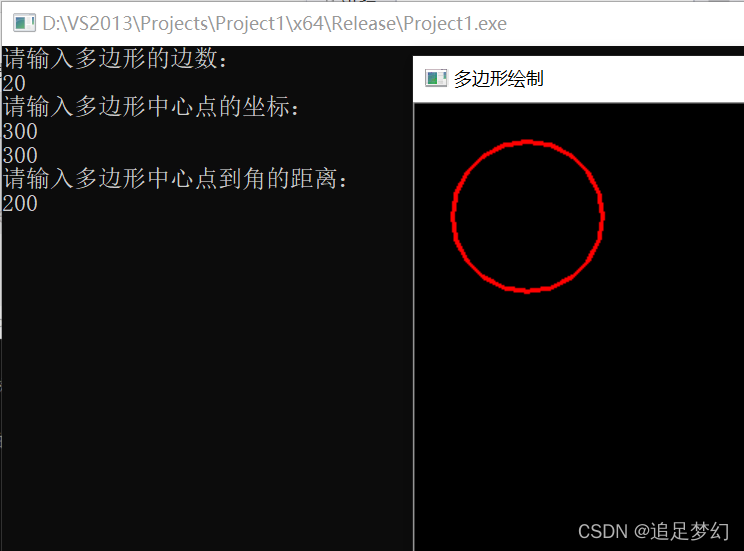
OpenCV 学习笔记-day16 正多边形绘制demo
OpenCV 学习笔记 day16 随机数与随机颜色 day16 随机数与随机颜色 给定边数n,中点坐标Point p;p.a(横坐标),p.b(纵坐标)和中点到顶点的距离d, 来绘制多边形 首先确定多边形每一条边的旋转角度 angle,并转成弧度制,这个角度指的是中点到顶点连线与x轴的夹角 double angle = 360.0 / n / 180.0PI; 找到顶点坐标