蓝桥备赛——矩阵读入

本文主要是介绍蓝桥备赛——矩阵读入，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述 

如上图所示，是一道有关二维前缀和的问题，因为涉及到二维，肯定就是以矩阵的形式进行读入的。

为此，针对矩阵的读入形式进行总结，可以大致总结出两种类型如下：

二维列表推导式

n, m, k = map(int, input().split())
mat = []
for i in range(n):mat.append(list(map(int, input().split())))
pre = [[0 for _ in range(m)] for _ in range(n + 1)]
for i in range(1, n + 1):for j in range(m):pre[i][j] = pre[i - 1][j] + mat[i - 1][j]

 可以看到上面代码的

pre = [[0 for _ in range(m)] for _ in range(n + 1)]

表示的是对于第一个[ ]中的元素是生成一个行向量，对于外面的第二个[ ]表示的是生成多少行的列表。

经过上面的代码，可以获得一个列表为

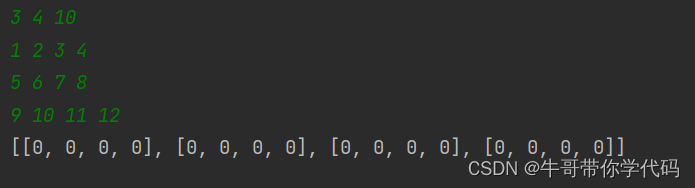
即获得了一个所有元素都为0的列表。后面再不停地读入元素进行原内容覆盖。

自创的方法

n,m,k=map(int,input().split())
mas=[]
for i in range(n):matrix = []matrix.extend(map(int,input().split()))mas.append(matrix)
print(mas)

 同样是先读入数据，不过需要额外创建一个列表作为中转，将数据读入后，再将其作为整体append到一个新的列表，即可达到上面二维列表推导式的效果。

与上面方法不同的地方是，不需要再重新将元素全部覆盖，所录入列表的即为最终数据。

AC Code

n, m, k = map(int, input().split())
mat = []
for i in range(n):mat.append(list(map(int, input().split())))
pre = [[0 for _ in range(m)] for _ in range(n + 1)]
for i in range(1, n + 1):for j in range(m):pre[i][j] = pre[i - 1][j] + mat[i - 1][j]
ans = 0
for i in range(n):for j in range(i, n):l, r, sum = 0, 0, 0while r < m:sum += pre[j + 1][r] - pre[i][r]while sum > k:sum -= pre[j + 1][l] - pre[i][l]l += 1ans += r - l + 1r += 1
print(ans)

现在来解释一下上面的代码

n, m, k = map(int, input().split())
mat = []
for i in range(n):mat.append(list(map(int, input().split())))
pre = [[0 for _ in range(m)] for _ in range(n + 1)]
for i in range(1, n + 1):for j in range(m):pre[i][j] = pre[i - 1][j] + mat[i - 1][j]

这块代码的作用就是读入相关数据

ans = 0
for i in range(n):for j in range(i, n):l, r, sum = 0, 0, 0while r < m:sum += pre[j + 1][r] - pre[i][r]while sum > k:sum -= pre[j + 1][l] - pre[i][l]l += 1ans += r - l + 1r += 1
print(ans)

上面代码的作用就是对应：

for i in range(1, n + 1): for j in range(m): pre[i][j] = pre[i - 1][j] + mat[i - 1][j]：计算前缀和矩阵pre。对于pre[i][j]，表示原始矩阵中第i-1行（因为前缀和矩阵行数比原始矩阵多了1）以及前j列的元素之和。

ans = 0：初始化变量ans，用于记录满足条件的子矩阵数量。

for i in range(n): for j in range(i, n):：遍历所有可能的子矩阵的上边界i和下边界j。

l, r, sum = 0, 0, 0：初始化左边界l、右边界r以及子矩阵元素之和sum。

while r < m: sum += pre[j + 1][r] - pre[i][r]：在子矩阵的右边界r小于列数m时，计算子矩阵在当前列的元素之和。

while sum > k: sum -= pre[j + 1][l] - pre[i][l] l += 1：如果子矩阵的元素之和超过了限定值k，则移动左边界l，直到子矩阵的元素之和不再超过k。

ans += r - l + 1：更新满足条件的子矩阵数量。

r += 1：向右移动子矩阵的右边界r。

print(ans)：输出满足条件的子矩阵数量。

该算法的时间复杂度为O(n^3 * m)，因为有三层嵌套循环分别遍历行、列和子矩阵。

 

这篇关于蓝桥备赛——矩阵读入的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---