本文主要是介绍线性CCD,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
线性CCD
综述:本文讲述了线性CCD是什么、由什么组成、工作原理、芯片TSL401的引脚和时序、线性CCD的时序。
1. 定义
线性CCD,只能采集一行像素,分辨率为128,也即是线性CCD≈128个光电传感器。经过光照时,光电二极管产生电流,再通过积分电路,转化为电压,就可以通过读取电压值来推出光照强度,再根据白色反射光照,黑色吸收光照,即可以知道地面黑色循迹线。
(思路:光照→吸收→电流低→电压低→是循迹路线)

2. 芯片TSL401
由于直接通过单片机读取CCD数据的话,需要读取128个数据,太占用单片机的IO口,于是运用了TSL401芯片。
(1)TSL401芯片引脚:

①电源引脚:VCC接高电平(3.3/5),GND接地
②信号引脚:AO是输出引脚,通过ADC读取AO就可以得到电压值;CLK是时钟引脚,SI是串行输入引脚,通过单片机的IO引脚控制CLK和SI的高低电平来模拟时序的高低就可以获取信息了。
(2)TSL401芯片时序图

①采集开始:CLK为上升沿,SI为高电平(不少于20us)且在CLK为下个高电平时为0
②数据采集:从采集信号开始后,采集128个数据
③采集结束:第129个CLK标志采集结束(不可以只有128个CLK),可以不采集了,也可以再次进行数据采集,但是再次采集需要将间隔20us(将数据从寄存器移到IO的最短时间)
④积分复位:采集开始的前18个周期不进行积分,只进行积分电容的电荷释放(积分复位)
⑤积分:采集开始的第19个周期开始积分
3. 线性CCD的功能框图
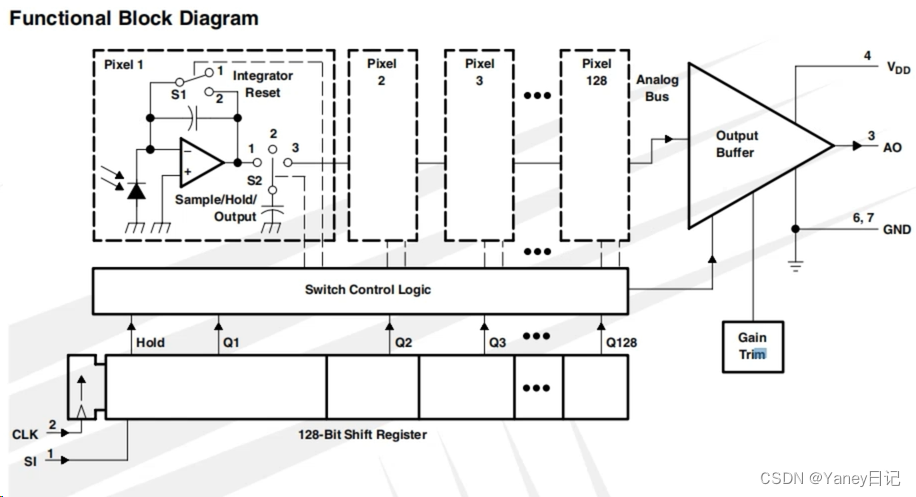
(1)上面电路讲解
①Pixel是一个像素电路,光电二极管收到光照后产生光电流,通过运算放大器将电压转到1脚。
②当S1接到1时,像素开始积分;当S1接到2时,积分开始复位,释放电荷。
③S2接到1时,采样电容与积分电路相连接,S2接到2时,采样电容进行电荷的保持,S2接到3时,采样电容与数据输出的运算放大器(后面的那个运算放大器)相连接,AO就可以输出数据。
(2)下面电路讲解
下面是数据寄存器。
(有点难理解,需要多读几遍)
①SI为高,CLK为时钟上升沿时发出“hold”信号,S1开关由1接到2,进行积分的复位;同时,S2开关由1接到2,进行了采样电荷的保持。
②当下一个CLK上升沿到达后,Q1为1(高电平),S2开关由2接到3,与后面的运算放大器相连接,即可以在AO口读取数据值。
③当下一个CLK上升沿到达后,Q1的数据就会移动到Q2,相应的像素2的S2就会从2接到3,像素1的S2从3接到2,以此类推。(也就是一个一个往后推)
④当前18个数据周期完毕后,完成积分复位,S1从2接到1,开始积分,前18个像素的S2从2接到1,开始积分。
⑤当第19个CLK上升沿到达后,第19个像素的S2从2接到3,接到AO口,同时,第18个像素的S1就会从2接到1进行积分。
⑥依次将128个数据处理完,128个CLK周期读取了128个数值,但是第128个像素的S2仍然在3上,没有接到1上进行积分,所以,最低需要129个CLK周期结束采集。
(3)积分时间
积分时间是积分器中电容的充电时间,积分时间越长,AO输出的电压范围越大,黑色与白色就可以区分得更明显,但是,积分时间太长会小车导致采集数据得时间变长,不不易于操控小车。
积分时间=完整周期时间-18个CLK周期时间
完整周期时间=129个CLK周期时间+距离下次采样的时间。
改变积分时间:控制两次采样之间的时间
4. 学习视频
CCD学习视频
侵权联系删除!
这篇关于线性CCD的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!