本文主要是介绍支持向量机（一）线性可分的支持向量机与硬间隔最大化，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
支持向量机其实和感知机的模型思想挺相似的，都是找出一个分离超平面对数据进行二分类。它是定义在特征空间上的间隔最大的线性分类器，这个间隔最大化使它区别于感知机；感知机通过迭代算法找出的分离超平面可以是不唯一的，但是支持向量机由于有最大化间隔的限制，即所有的支持向量点到分离超平面的距离之和是最大的，所以它的分离超平面是唯一的；实际上支持向量机还有核技巧，即数据本来是非线性可分的，但是通过映射（核技巧）将其转化为线性可分，所以它也是个非线性分类器。
感知机必须对线性可分的数据集有效，但是支持向量机不仅对线性可分的数据有效，也对线性不可分的数据有效；其可以分为三种情况：
- 当数据线性可分的时候，通过硬间隔最大化产生线性可分的支持向量机，也叫硬间隔支持向量机）。
- 当数据线性近似可分的时候，通过软件各最大化产生线性支持向量机，也叫软件各支持向量机。
- 当数据线性不可分的时候，通过核技巧即软件各最大化，学习非线性支持向量机。
我们这里先介绍线性可分的支持向量机。
- 函数间隔
对于线性可分的支持向量机，我们需要找出一个超平面（对于二维的数据就是一条直线），将所以的数据点分开，就如下图所示：
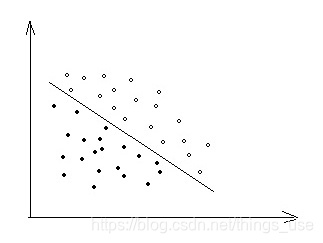
中间的那条直线，就是我们需要求的直线L:
。对于点xi，如果wxi+b>0，则我们可以判断点在直线的上方，如果wxi+b<0则我们可以判断点在直线的下方，其中|wxi+b|可以相对的表示点到直线的远近，越远我们就可以认为对这个分类结果越确信。其中wx+b的符号与类标记y的符号是否一致能够表示分类是否正确。假设对于对于所有的样本点（xi,yi）都分类正确，则yi的符号和wxi+b的符号是相同的yi(wxi+b)>0，否则是相反的yi(wxi+b)<0，所以我们可以用
来表示分类的正确性以及确信度ÿ
这篇关于支持向量机（一）线性可分的支持向量机与硬间隔最大化的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
