本文主要是介绍Leetcode70. 爬楼梯(动态规划),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Leetcode原题
Leetcode70. 爬楼梯
标签
记忆化搜索 | 数学 | 动态规划
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?示例 1:输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
提示:1 <= n <= 45
题目分析
我们用 f(x) 表示爬到第 x 级台阶的方案数,考虑最后一步可能跨了一级台阶,也可能跨了两级台阶,所以我们可以列出如下式子:
f(x)=f(x−1)+f(x−2)
它意味着爬到第 x 级台阶的方案数是爬到第 x−1 级台阶的方案数和爬到第 x−2 级台阶的方案数的和。很好理解,因为每次只能爬 1 级或 2 级,所以 f(x) 只能从 f(x−1) 和 f(x−2) 转移过来,而这里要统计方案总数,我们就需要对这两项的贡献求和。
以上是动态规划的转移方程,下面我们来讨论边界条件。我们是从第 0 级开始爬的,所以从第 0 级爬到第 0 级我们可以看作只有一种方案,即 f(0)=1;从第 0 级到第 1 级也只有一种方案,即爬一级,f(1)=1。这两个作为边界条件就可以继续向后推导出第 n 级的正确结果。我们不妨写几项来验证一下,根据转移方程得到 f(2)=2,f(3)=3,f(4)=5,……,我们把这些情况都枚举出来,发现计算的结果是正确的。
我们不难通过转移方程和边界条件给出一个时间复杂度和空间复杂度都是 O(n) 的实现,但是由于这里的 f(x) 只和 f(x−1) 与 f(x−2) 有关,所以我们可以用「滚动数组思想」把空间复杂度优化成 O(1)。下面的代码中给出的就是这种实现。
题目实现
JAVA
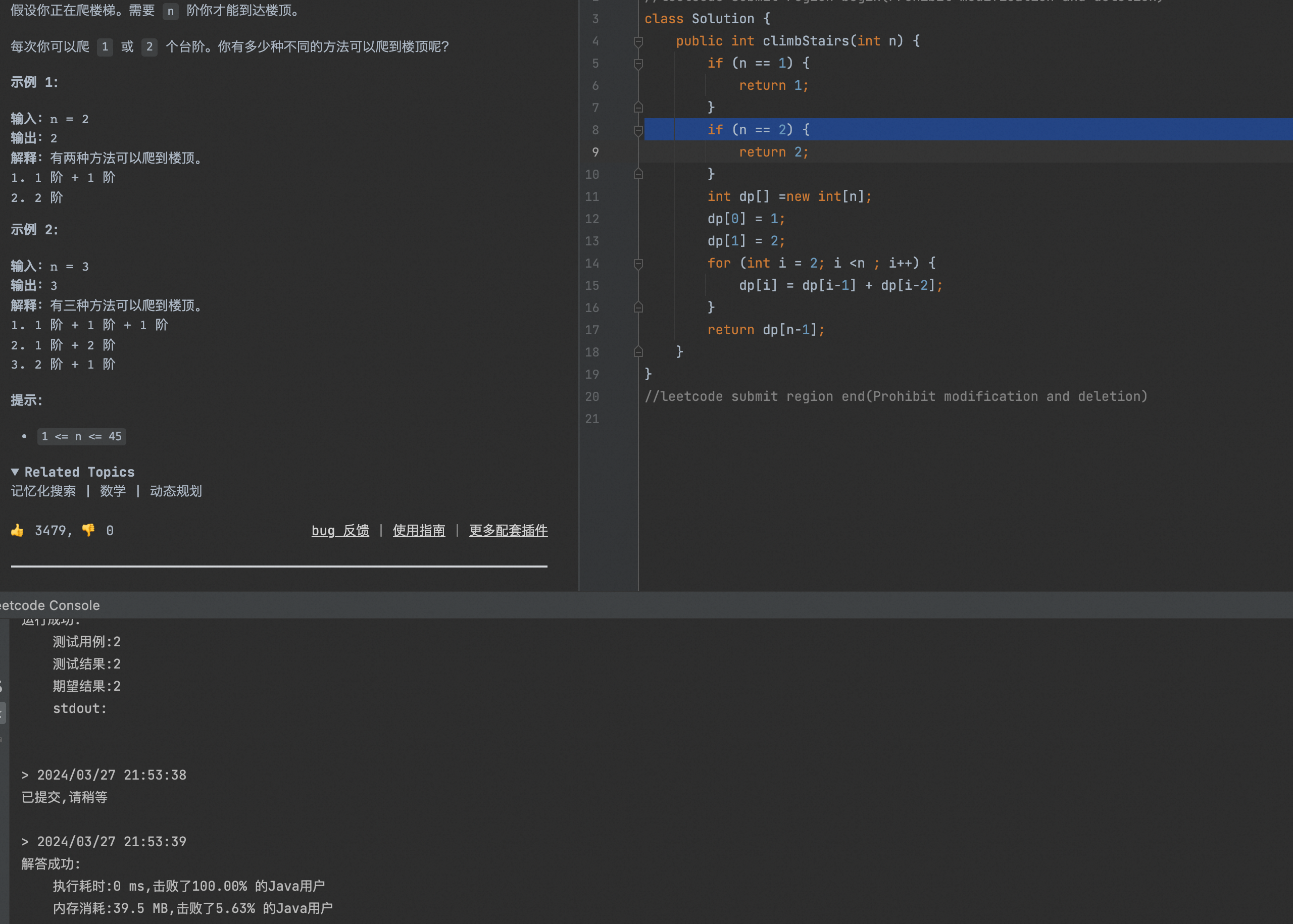
class Solution {public int climbStairs(int n) {if (n == 1) {return 1;}if (n == 2) {return 2;}int dp[] =new int[n];dp[0] = 1;dp[1] = 2;for (int i = 2; i <n ; i++) {dp[i] = dp[i-1] + dp[i-2];}return dp[n-1];}
}
C++
class Solution {
public:int climbStairs(int n) {int p = 0, q = 0, r = 1;for (int i = 1; i <= n; ++i) {p = q; q = r; r = p + q;}return r;}
};C
int climbStairs(int n) {int p = 0, q = 0, r = 1;for (int i = 1; i <= n; ++i) {p = q;q = r;r = p + q;}return r;
}GoLang
func climbStairs(n int) int {p, q, r := 0, 0, 1for i := 1; i <= n; i++ {p = qq = rr = p + q}return r
}其他
相似题
- 使用最小花费爬楼梯 1358
- 统计构造好字符串的方案数 1694
这篇关于Leetcode70. 爬楼梯(动态规划)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









